算法
无源汇上下界可行流
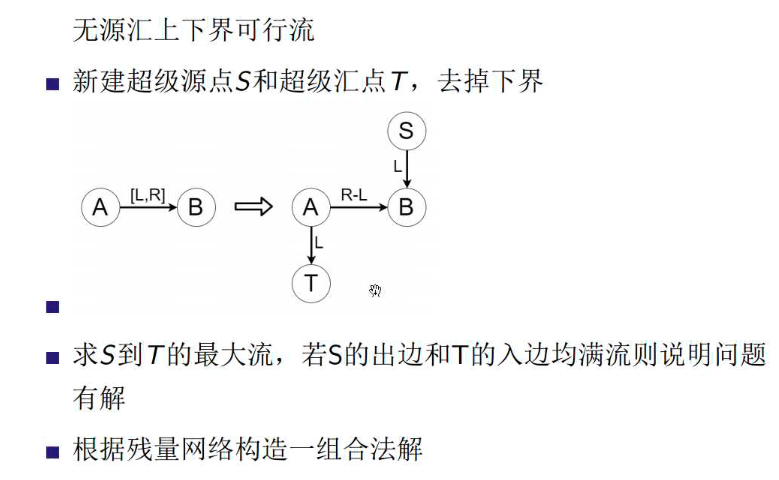
先强制流过l的流量
从s到每个正权点连流量为l的流量
从每个负权点向t连-l的流量
如果容量为0,则不连边
有源汇上下界最大流
去掉下界

先求出可行流
再求S到T的最大流
有源汇上下界最小流

直接应用
poj1149

我的思路
建一个点S,到每个顾客,连INF的边,每个顾客
正解
1.用分层图,建n*m个点
2.直接从S向每个人连边,记录下每个猪圈打开的人的先后顺寻,先来的人向后来的人连边
BZOJ2406

Solution


路径覆盖模型
路径覆盖无交集
链覆盖可以有交集

起点,终点的度数都为1
最小化$n-sum{d}$=最大化$sum{d}$d为入度
把原图的点都进行拆点
路径覆盖:
若i,j有边,则从i到j'连边
所有边的边权均为1
链覆盖:
用floyd求传递闭包
从一个点向它能到达的点都连边
用最小流解决
链覆盖把每个点的上限改为INF
魔术球问题

Solution

CTSC2006

最小链覆盖

Dilworth定理

例如<=号
自反性:x<=x
反对称性:x<=y , y<=x —>x==y
传递性:x<=y,y<=z—>x<=z
(<,>不满足偏序关系,不满足第二条性质)
(DAG满足偏序关系,有向图不满足)

反链:两点之间不能相互到达
定理:

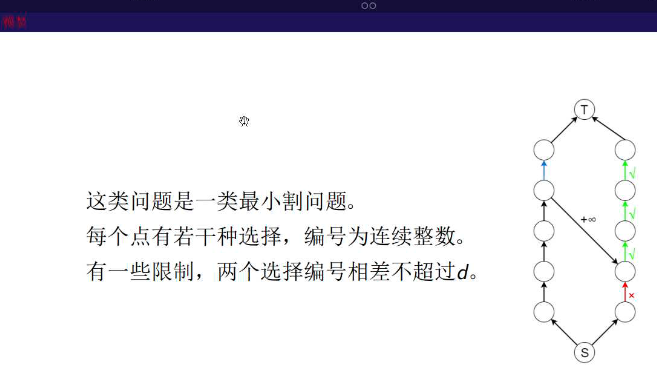
TJOI2016XX数学

暴力
拆成n*m个点,每个点的权值下界为给定的权值,上界为INF
优化

对所有点选一条点权和最大的
从左下到右上DP
时间分层

网络流24题星际XXXX

当最大流为k的时候结束

[HNOI2007]紧急疏散

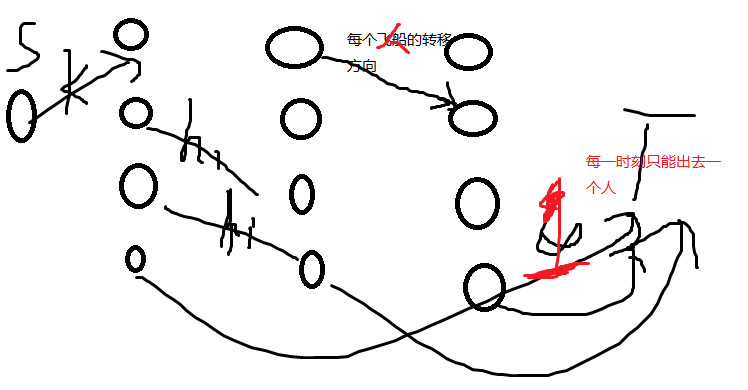
回路限制
POI2010

solution

给每条边定向&&判断是否连通
每条边定向后会使一个点的入度加1,会使一个点的入度减1
先随便定向并保留一次反向机会

可以把每次反向看成一条权值为2的增广路

把点权预先除以二,验证图是否能满流
BZOJ4215
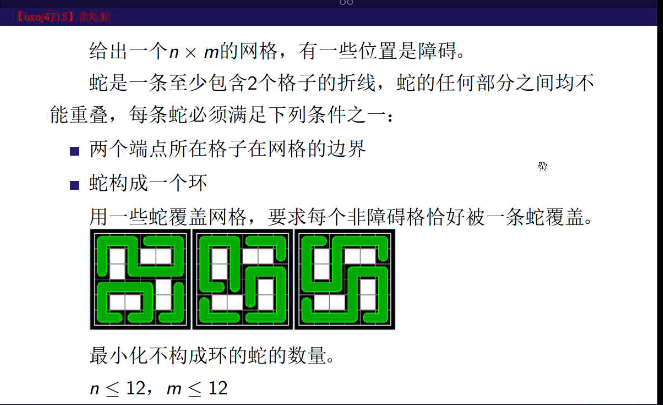
对一个网格进行黑白染色,搞成二分图
用流量为2的边去限制度数为2
如果图满流,那么就存在所有蛇都构成环的方案
找方案的时候看哪些边满流了
如果蛇不构成环,
对于边界上的点,设置其权值为[1,2],对于非边界上的点,其权值为[2,2]
求最大流

最大权闭合子图
模型
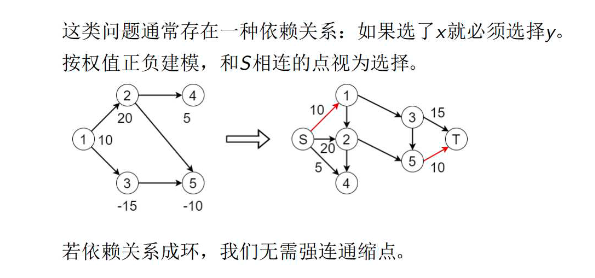
所有与S相连的点视为不选择
所有与T相连的点视为选择
有环的情况可以不缩点,(缩点也可以)
TJOI2015 线性代数

Bij*Ai*Aj
Ci*Ai
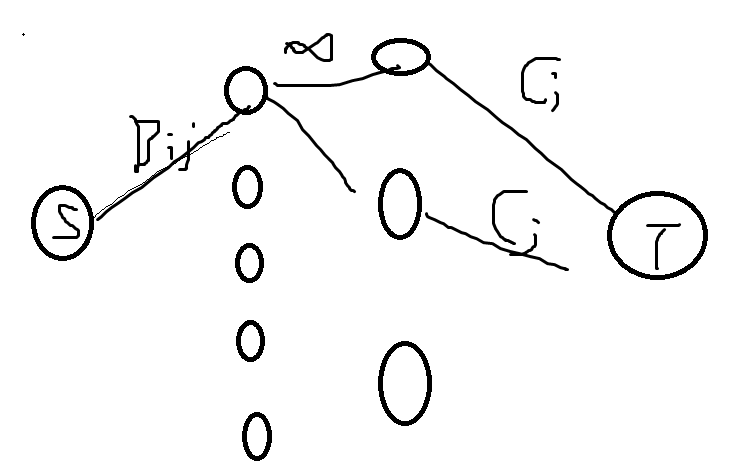
COdefoeceXXX

若不考虑限制条件
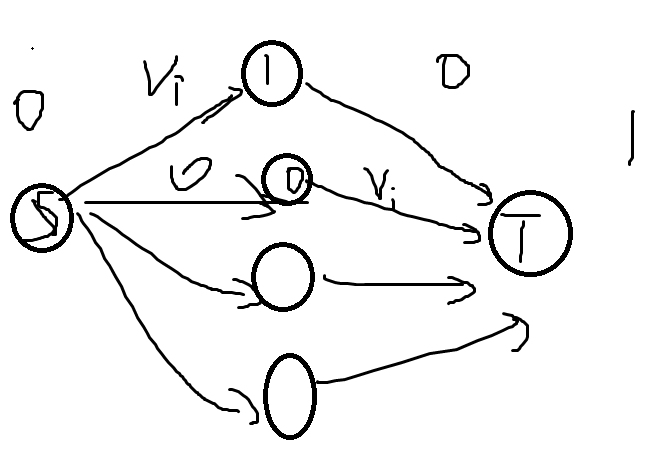
限制条件
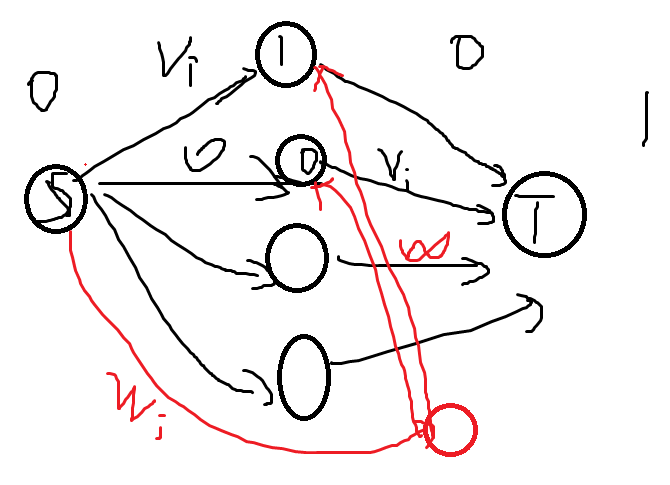
从S向新加的点连Wi边
从新加的点向中间的三个点连INF的边
CEOI?



转化为最小割
BZOJ3774


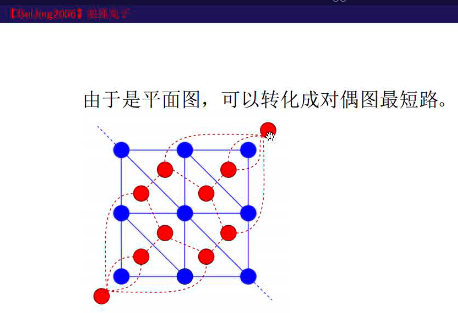
平面图对偶图
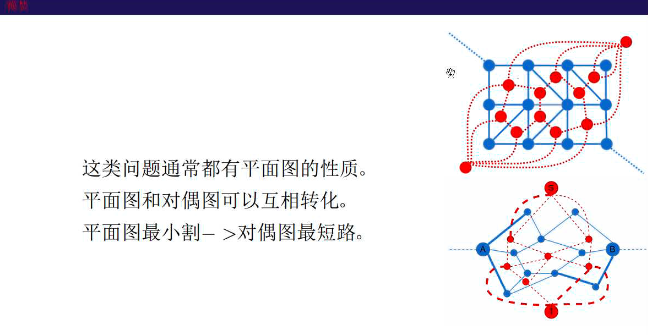
狼抓兔子
NOI2010海拔


相当于S和T之前求最小割

距离限制
HNOI拍照


变形


CTSC2009

根据曼哈顿距离的性质
分别最优化横纵坐标


Hall定理

k-完备匹配

首先,贪心的找最大匹配然后删去是显然不对的

证明
想要证明k-正则二分图,只需证明k-1是否存在
假设不存在
左侧的m*k条边若分给右侧<m条边,则有一条边的度数不为1
做法

若原图不存在k-正则二分图则无解
POI2009 Lyz


tag
【CERC2016】Bipartite Blanket
solution

证明



时间复杂度
$2^n*n+2^n*log n$
