《数学练习》

P2158 [SDOI2008] 仪仗队:

一开始还确实没来思路，但是昨晚看了一个水题也是用到了斜率，所以就想到了斜率。

很明显斜率相同的会被遮挡，也就是说不是最简分数的形式就会被遮挡。

很显然求一下互质的坐标数就行。

这里的话左下角那个人是不算的，然后我们要以左下角为(0,0)点来看才对。

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> pii;
const int N = 4e4 + 5;
const int M = 2e4 + 5;
const double eps = 1e-10;
const LL Mod = 1e9 + 7;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    int f = 1;int x = 0;char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

bool vis[N];
int prime[N],tot = 0,phi[N];
void init() {
    for(int i = 2;i < N;++i) {
        if(!vis[i]) {
            prime[++tot] = i;
            phi[i] = i - 1;
        }
        for(int j = 1;j <= tot && prime[j] * i < N;++j) {
            vis[prime[j] * i] = 1;
            if(i % prime[j] == 0) {
                phi[i * prime[j]] = phi[i] * prime[j];
                break;
            }
            else phi[i * prime[j]] = phi[i] * phi[prime[j]];
        }
    }
}
void solve() {
    init();
    int n;n = read();
    if(n == 1) printf("0
");
    else {
        LL ans = 1LL * (n - 1) * (n - 1) + 3;
        for(int i = 2;i < n;++i) {
            ans -= (i - phi[i] - 1) * 2 + 1;
        }
        printf("%lld
",ans - 1);
    }

}
int main() {
    solve();
    system("pause");
    return 0;
}

P2398 GCD SUM:

测评机炸了一会..

这题有好几种推法来着。

$sum_{d = 1}^{n}sum_{i = 1}^{n}sum_{j = 1}^{n} d * [gcd(i,j) = d]$

$sum_{d=1}^{n}dsum_{i=1}^{frac{n}{d}}sum_{j=1}^{frac{n}{d}} [gcd(i,j)=1]$

$sum_{d = 1}^{n}dsum_{t = 1}^{left lfloor frac{n}{d} ight floor} mu (t) * [frac{n}{dt}] *left lfloor frac{n}{dt} ight floor$

后面可以代换一个n / d = T然后就是一个T / t的求和，可以发现这里两重是调和级数，所以我们第二维暴力算也是可以的。

我这里写的整除分块。

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> pii;
const int N = 1e5 + 5;
const int M = 2e4 + 5;
const double eps = 1e-10;
const LL Mod = 1e9 + 7;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    int f = 1;int x = 0;char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

bool vis[N];
int prime[N],tot = 0,mu[N];
void init() {
    mu[1] = 1;
    for(int i = 2;i < N;++i) {
        if(!vis[i]) {
            prime[++tot] = i;
            mu[i] = -1;
        }
        for(int j = 1;j <= tot && prime[j] * i < N;++j) {
            vis[prime[j] * i] = 1;
            if(i % prime[j] == 0) break;
            else mu[i * prime[j]] = -mu[i];
        }
    }
    for(int i = 1;i < N;++i) mu[i] += mu[i - 1];
}
LL cal(int x) {
    LL sum = 0;
    for(int L = 1,r = 0;L <= x;L = r + 1) {
        r = x / (x / L);
        sum += 1LL * (x / L) * (x / L) * (mu[r] - mu[L - 1]);
    }
    return sum;
}
void solve() {
    int n;n = read();
    LL ans = 0;
    for(int d = 1;d <= n;++d) ans += cal(n / d) * d;
    printf("%lld
",ans);
}
int main() {
    init();
    solve();
    system("pause");
    return 0;
}

P6028 算术:

一开始想的是杜教筛方向的，因为感觉怎么样都要杜教筛做。

但是没想到后面那个式子可以化简开来。

这里有一步非常巧妙的推算：

$(p - 1) sum_{j = 0}^{alpha (i)}p^{j} = (p^1 - p) + (p^2 - p^1) + ... + (p ^ {(alpha (i) + 1)} - p ^ {alpha (i)}) = p ^ {(alpha (i) + 1)} - 1$

然后就可以化简这个式子了。

上下都提取一下(p - 1)最后就是$frac{prod_{i = 1}^{k}sum_{j = 0}^{alpha (i)}p^j}{n}$

对上面整体展开可以分析一下，都是n的各个素因子的乘积组成的数，且幂次都<=n，那么显然这就是n的因子和。就有下面的化简。

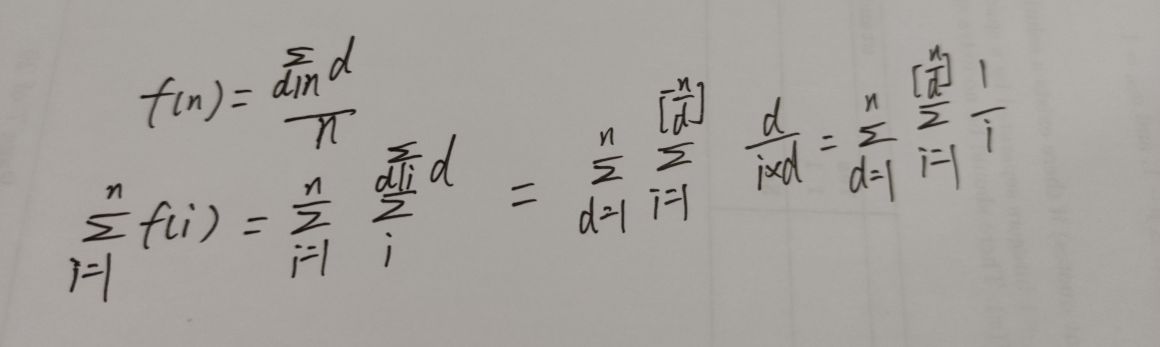
 这里我们小范围内可以求一下1 / i的前缀和。

大范围内有近似操作1 / n的前缀和可以近似为lg(n) + y,y约等于0.5772156649

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<LL,int> pii;
const int N = 1e7 + 5;
const int M = 7e5 + 5;
const double eps = 1e-10;
const LL Mod = 1e9 + 7;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    int f = 1;int x = 0;char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

long double sum[N];
void init() {
    for(int i = 1;i < N;++i) sum[i] = sum[i - 1] + 1.0 / i; 
}
long double cal(LL x) {
    if(x >= N) return log(x) + 0.5772156649;
    else return sum[x];
}
void solve() {
    init();
    LL n;scanf("%lld",&n);
    long double ans = 0;
    for(LL L = 1,r = 0;L <= n;L = r + 1) {
        r = n / (n / L);
        ans += cal(n / L) * (r - L + 1);
    }
    printf("%.10Lf
",ans);
}
int main() {
    solve();
   // system("pause");
    return 0;
}

P3807 【模板】卢卡斯定理/Lucas 定理:

Lucas定理模板题：当模数p<n，可以利用Lucas定理：

C(n,m) = C(n / p,m / p) + C(n % p,m % p).

思想就是对每段%p相同的进行分段处理。

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> pii;
#define rg register
const int N = 1e5 + 5;
const int M = 2e4 + 5;
const double eps = 1e-10;
const LL Mod = 1e9 + 7;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    rg int f = 1,x = 0;rg char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

LL f[N],inv[N];
LL quick_mi(LL a,LL b,LL p) {
    LL re = 1;
    while(b) {
        if(b & 1) re = re * a % p;
        b >>= 1;
        a = a * a % p;
    }
    return re;
}
void init(int p) {
    f[0] = 1;
    for(int i = 1;i < p;++i) f[i] = f[i - 1] * i % p;
    inv[p - 1] = quick_mi(f[p - 1],p - 2,p);
    for(int i = p - 2;i >= 0;--i) inv[i] = inv[i + 1] * (i + 1) % p;
}
LL C(LL n,LL m,LL p) {
    return f[n] * inv[m] % p * inv[n - m] % p;
}
LL Lucas(LL n,LL m,LL p) {
    if(m == 0) return 1;
    return Lucas(n / p,m / p,p) * C(n % p,m % p,p) % p;
}
void solve() {
    int n,m,p;n = read(),m = read(),p = read();
    init(p);
    printf("%lld
",Lucas(n + m,n,p));
}
int main() {
    int ca;ca = read();
    while(ca--) {
        solve();
    }
    //system("pause");
    return 0;
}

UVA294 约数 Divisors：

可以看到r - L的范围非常小，所以可以遍历这个区间，主要就是对每个数的因子个数的求解。

普通的做法需要sqrt(n)的复杂度，显然会TLE。

这里可以利用：

约数(因子)个数定理：对于一个数n，质因子分解为$prod_{i = 1}^{k}pi^{ki}$

那么他的约数个数为$prod_{i = 1}^{k}(ki + 1)$

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> pii;
#define rg register
const int N = 1e5 + 5;
const int M = 2e4 + 5;
const double eps = 1e-10;
const LL Mod = 1e9 + 7;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    rg int f = 1,x = 0;rg char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

bool vis[N];
int prime[N],tot = 0;
void init() {
    for(int i = 2;i < N;++i) {
        if(!vis[i]) prime[++tot] = i;
        for(int j = 1;j <= tot && prime[j] * i < N;++j) {
            vis[prime[j] * i] = 1;
            if(i % prime[j] == 0) break;
        }
    }
}
int a[N];
void solve() {
    init();
    int n;n = read();
    while(n--) {
        LL L,r;scanf("%lld %lld",&L,&r);
        LL ans = 0,mx = 0;
        for(LL i = L;i <= r;++i) {
            int x = i,len = 0;
            for(int j = 1;j <= tot;++j) {
                if(x % prime[j] == 0) {
                    int cnt = 0;
                    while(x % prime[j] == 0) x /= prime[j],++cnt;
                    a[++len] = cnt;
                }
            }
            LL ma = 1;
            for(int j = 1;j <= len;++j) ma *= (a[j] + 1);
            if(i == 1 && ma > mx) mx = ma,ans = i;
            if(len != 0 && ma > mx) mx = ma,ans = i;
        }
        printf("Between %lld and %lld, %lld has a maximum of %lld divisors.
",L,r,ans,mx);
    }
}
int main() {
    solve();
    //system("pause");
    return 0;
}

P2424 约数和：

推错了式子结果写成了杜教筛..不过这题确实可以杜教筛做的。

其实题目就是$sum_{i = 1}^{n}sum_{d | i}^{}d$

化简得:$sum_{d = 1}^{n}d * sum_{i = 1}^{frac{n}{d}} = sum_{d = 1}^{n}d * frac{n}{d}$

整除分块即可。

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> pii;
#define rg register
const int N = 1e5 + 5;
const int M = 2e4 + 5;
const double eps = 1e-10;
const LL Mod = 1e9 + 7;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    rg int f = 1,x = 0;rg char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

LL check(LL n) {
    LL sum = 0;
    for(LL L = 1,r = 0;L <= n;L = r + 1) {
        r = n / (n / L);
        sum += 1LL * (r + L) * (r - L + 1) / 2 * (n / L);
    }
    return sum;
}
void solve() {
    LL x,y;scanf("%lld %lld",&x,&y);
    printf("%lld
",check(y) - check(x - 1));
}
int main() {
    solve();
    //system("pause");
    return 0;
}

P3758 [TJOI2017]可乐：

很显然有个dp[i][j] - 第i秒在j位置的方案数，但是这里复杂度差不多M * t,究极卡常才能勉强冲过去。

然后我们考虑一下自爆的处理，连虚点0，然后停在原地的操作我们就连自环。

然后考虑去优化这个dp，我们发现如果我们用邻接矩阵来存图的话，dp就是关于邻接矩阵的一个递推。

转移矩阵就是这个邻接矩阵，所以我们可以矩阵快速幂加速t，这样复杂度就很低了。

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> pii;
const int N = 1e6 + 5;
const int M = 2e4 + 5;
const double eps = 1e-10;
const LL Mod = 2017;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    int f = 1,x = 0;char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

struct Mat{
    int m[31][31];
    Mat operator * (const Mat &a)const{
        Mat c;memset(c.m,0,sizeof(c.m));
        for(int k = 0;k <= 30;++k)
            for(int i = 0;i <= 30;++i)
                for(int j = 0;j <= 30;++j) c.m[i][j] = ADD(c.m[i][j],MUL(m[i][k],a.m[k][j]));
        return c;
    }    
};
Mat e;
Mat quick_Mat(Mat a,int b) {
    Mat re;memset(re.m,0,sizeof(re.m));
    for(int i = 0;i <= 30;++i) re.m[i][i] = 1;
    while(b) {
        if(b & 1) re = re * a;
        b >>= 1;
        a = a * a;
    }
    return re;
}
void solve() {
    int n,m;n = read(),m = read();
    while(m--) {
        int u,v;u = read(),v = read();
        e.m[u][v] = 1;    
        e.m[v][u] = 1;
    }
    for(int i = 1;i <= n;++i) e.m[i][0] = 1;
    for(int i = 0;i <= n;++i) e.m[i][i] = 1;
    int t;t = read();
    Mat a = e;
    Mat ans;memset(ans.m,0,sizeof(ans));
    ans.m[0][1] = 1;
    a = quick_Mat(a,t);
    ans = ans * a;
    int ma = 0;
    for(int i = 0;i <= n;++i) {
        ma = ADD(ma,ans.m[0][i]);
    }
    printf("%d
",ma);
}
int main() {
    solve();
    return 0;
}

P6561 [SBCOI2020] 人：

首先考虑dp，但是发现dp复杂度和空间都实现不了。

然后我们对这题进行转化。

2 *i 和 2*i - 1看成一组，显然这一组两个位置不能都选。

我们把这一组选了2 * i - 1位置看成A，选了2 * i看成B，都没选看成C

那么题目就转化成了由A,B,C组成的长度为m的字符串，且不能包含子串BA。

A有a个,B有b个，C有m - a - b个。

也就是说对于A，它不能放在B字符的后面。

那么我们先考虑B,C两个的排列。

显然是C(m - a,b)。

我们再考虑此时A的能放置的位置。

第一个A：最前面或者所有C的后面，即1 + m - a - b

第二个A：最前面或者所有C的后面，或者前一个A的后面，即1 + m - a - b + 1

那么第i个A：1 + m - a  - b + i - 1 = m - a - b + i.

所以a个A能放置的方案数为（m - a - b + 1） * (m - a - b + 2) **** (m - a - b + a).

令m - a - b = n，即为(n + 1) * (n + 2) * .. (n + a) = (n + a)! / n!

因为这里所有a都是等价的，所以需要去重复的方案数，即除以a!

得(n + a)! / (n! * a!).仔细看这个不就是C(n + a,a)吗..
然后就可以做了.C(n + a,a) = C(m - b,a)。//n代换掉

所以最后ans = C(m - a,b) * C(m - b,a).

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> pii;
const int N = 1e6 + 5;
const int M = 2e4 + 5;
const double eps = 1e-10;
const LL Mod = 998244353;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    int f = 1,x = 0;char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

LL f[N],inv[N];
LL quick_mi(LL a,LL b) {
    LL re = 1;
    while(b) {
        if(b & 1) re = re * a % Mod;
        b >>= 1;
        a = a * a % Mod;
    }
    return re;
}
void init() {
    f[0] = 1;
    for(int i = 1;i < N;++i) f[i] = f[i - 1] * i % Mod;
    inv[N - 1] = quick_mi(f[N - 1],Mod - 2);
    for(int i = N - 2;i >= 0;--i) inv[i] = inv[i + 1] * (i + 1) % Mod;
}
LL C(LL n,LL m) {
    return f[n] * inv[m] % Mod * inv[n - m] % Mod;
}
void solve() {
    int m,a,b;m = read(),a = read(),b = read();
    LL ans = C(m - a,b) * C(m - b,a) % Mod;
    printf("%lld
",ans);
}
int main() {
    init();
    int ca;ca = read();
    while(ca--) {    
        solve();
    }
    return 0;
}

P3455 [POI2007]ZAP-Queries:

回顾一下.

 $sum_{i = 1}^{a}sum_{j = 1}^{b}[gcd(i,j) = d] -> sum_{i = 1}^{[frac{a}{d}]}sum_{j = 1}^{[frac{b}{d}]}[gcd(i,j) = 1]$

改为枚举约数即可，这里有一点，就是因为有两段的分块，我们是一起分块的，所以每次取右界，要取近的，这样保证两段都是满足n / L,m / L都是对于他们自己的那段一样的。

// Author: levil
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> pii;
const int N = 5e4 + 5;
const int M = 2e4 + 5;
const double eps = 1e-10;
const LL Mod = 998244353;
#define pi acos(-1)
#define INF 1e9
#define dbg(ax) cout << "now this num is " << ax << endl;
inline int read() {
    int f = 1,x = 0;char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9'){x = (x<<1)+(x<<3)+(c^48);c = getchar();}
    return x*f;
}
inline long long ADD(long long x,long long y) {return (x + y) % Mod;}
inline long long DEC(long long x,long long y) {return (x - y + Mod) % Mod;}
inline long long MUL(long long x,long long y) {return x * y % Mod;}

int mu[N],prime[N],tot = 0;
bool vis[N];
void init() {
    mu[1] = 1;
    for(int i = 2;i < N;++i) {
        if(!vis[i]) {
            prime[++tot] = i;
            mu[i] = -1;
        }
        for(int j = 1;j <= tot && prime[j] * i < N;++j) {
            vis[prime[j] * i] = 1;
            if(i % prime[j] == 0) {
                break;
            }
            else mu[prime[j] * i] = -mu[i];
        }
    }
    for(int i = 1;i < N;++i) mu[i] += mu[i - 1];
}
void solve() {
    int a,b,d;a = read(),b = read(),d = read();
    int n = a / d,m = b / d;
    int up = min(n,m);
    LL ans = 0;
    for(int L = 1,r = 0;L <= up;L = r + 1) {
        r = min(n / (n / L),m / (m / L));
        ans += 1LL * (mu[r] - mu[L - 1]) * (n / L) * (m / L);
    }
    printf("%lld
",ans);
}
int main() {
    init();
    int ca;ca = read();
    while(ca--) {
        solve();
    }
    return 0;
}