Armstrong公理系统
逻辑蕴涵
定义/解释
比如A->B B->C 在关系模型R<U,F>中成立,可以得到A->C字R中也成立,所以称F逻辑蕴含A->C。
闭包
定义/解释
在关系模型R中,F所逻辑蕴涵的所有函数依赖叫做F的闭包,记为(F^{+})。
某个属性集关于依赖集的闭包
定义/解释
即已有X这个属性集作为左部,通过依赖集F的所有函数依赖,可以推导出的所有函数依赖,称为X关于F的闭包,记为(X_F^{+})
例题
已知关系模型R<U,F>,其中U={A,B,C,D,E} F={AB->C,B->D,C->E,EC->B,AC->B},求((AB)_F^{+})。
算法:把AB作为左部,然后从F中找到左部是完全属于AB的,把对应的右部并到AB里,作为新的左部,重复直到不能再增加左部或者已经等于全集。
结果:((AB)_F^{+})=ABCDE
最小依赖集
例题
F={abd->e,ab->g,b->f,c->j,cj->i,g->h}
算法:
- 将右部有多个的拆开,比如ab->cd 变成 ab->c,ab->d
- 尝试删除左侧的冗余函数依赖,具体操作是对于每个函数依赖X->A,假设将该依赖删除,然后求X在剩下的依赖集中的闭包(X_G^{+}),如果A属于这个闭包,那么就可以删除。
- 尝试删除左侧的冗余属性,具体操作是对于剩下的每个有多个属性的函数依赖X->A,对于每个属性,假设将该属性删除,然后求剩下的属性集在F中的闭包((X-B_i)^{+}_F),如果A属于这个闭包,则可以删除。
结果:F={abd->e,ab->g,b->f,c->j,c->i,g->h}
求候选码
例题
已知关系模型R<U,F>,其中U=(A,B,C,D,E,G),F={AB-->C,CD-->E,E-->A.A-->G},求R的候选码。
算法:
- 找出只在函数依赖左部出现的属性集X,X肯定是任意一个候选码的成员,因为只在左边出现,所以少了它肯定推不出全集U。
- 只在右部出现,肯定不属于任何一个候选码。
- 其他的情况尝试组合求闭包,如果闭包是全集U,那么就是候选码。
结果:
只在左边出现的是B和D,所以确定了BD,只在右边出现的是G,所以排除G,剩下A,C,E。
先考虑一个的组合,ABD,BCD和BDE,三个的闭包都是全集U,所以三个都是候选码,算法结束。
模式分解
判断是否无损连接
算法
- 对于一个分解,有k个子集,n个属性,建立一张k行n列的初始表,对于每一行也就是分解的每个子集,把该分解子集出现的属性对应的列写上(a_j),否则写上(b_{ij})
- 对于每一个依赖,找到左部属性对应的列,根据行的值分组,对于行的值相同的这些行,查看对应右部属性的列,如果这些格子里有a值,那把所有这些格子改成a值,如果没有,改成行最小的b值。如果某个b值改成a值,那么其他行(不属于当前操作的行)的相同b值也要改成a值。
- 如果不变则停止,如果出现有一行为a1 a2 ... an,那么说明该连接为无损连接。
例题
已知R<U,F>,U={A,B,C,D,E},F={A→C,B→C,C→D,DE→C,CE→A},R的一个分解为R1(AD),R2(AB),R3(BE),R4(CDE),R5(AE),判断这个分解是否具有无损连接性。
- 根据每个分解的属性,构造出初始表
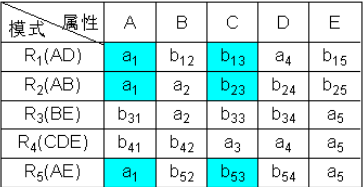
- 然后看第一个依赖A->C,找到A对应的第一列,其中1 2 5行的值相等,找到C对应的第三列,对应格子没有a值,所以全部改成(b_{13})。
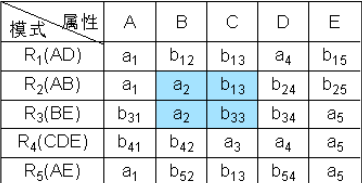
- 同理看第二个依赖,B->C,把(b_{33})改成(b_{13})。
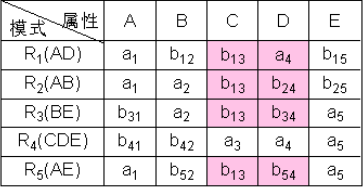
- 以此类推

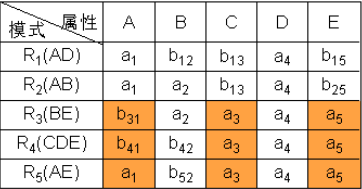
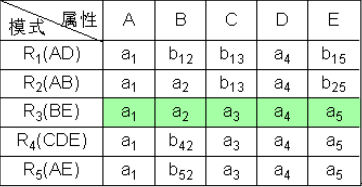
- 最后第三行有a1 a2 a3 a4 a5,所以该分解具有无损连接性。
3NF和保持函数依赖的分解
算法
- F=F的最小依赖集
- (U_0)={不在F出现的属性}
- U=U-(U_0)
- 若F中有函数依赖X->A,使得XA=U,那么分解就是R本身
- 如果没有,将剩下的F按左部分组,得到(U_i),分解就是{(R_1)<(U_1),(F_1)>,...} ∪ (R_0)<(U_0),(F_0)>
3NF和保持函数依赖和具有无损连接性的分解
算法
- 求出3NF和保持函数依赖的分解。
- X是R的码,让已有的分解∪上一个{(R^{*})<X,(F_X)>}。
- 如果分解中有某个(U_i)属于X,那么删掉该(U_i),如果X属于某个(U_i),那么删掉。
BCNF和具有无损连接性的分解
算法
- 类似递归的方法,首先判断自身是不是BC范式,如果是,无需分解。
- 否则,找到当前关系R的主码,找到一个左边不含主码的依赖X->A,设U1=A,分解出去,剩下的U2=U-{A}作为一个关系模式,继续重复上面的步骤。
- 根据X->A的选择的不同,得到的分解也是不同。
4NF和具有无损连接性的分解
算法
- 求出BCNF和具有无损连接性的分解。
- 对于一个关系R<U,F>,如果多值依赖X-->Y成立,则分解{R1<X,Y>,R2<X,Z>)}具有无损连接性,其中Z=U-X-Y。