Codefoces 791D. Bear and Tree Jumps 树形DP

D. Bear and Tree Jumps

 

A tree is an undirected connected graph without cycles. The distance between two vertices is the number of edges in a simple path between them.

Limak is a little polar bear. He lives in a tree that consists of n vertices, numbered 1 through n.

Limak recently learned how to jump. He can jump from a vertex to any vertex within distance at most k.

For a pair of vertices (s, t) we define f(s, t) as the minimum number of jumps Limak needs to get from s to t. Your task is to find the sum of f(s, t) over all pairs of vertices (s, t) such that s < t.

Input

The first line of the input contains two integers n and k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ 5) — the number of vertices in the tree and the maximum allowed jump distance respectively.

The next n - 1 lines describe edges in the tree. The i-th of those lines contains two integers ai and bi (1 ≤ ai, bi ≤ n) — the indices on vertices connected with i-th edge.

It's guaranteed that the given edges form a tree.

Output

Print one integer, denoting the sum of f(s, t) over all pairs of vertices (s, t) such that s < t.

 

input

13 3
1 2
3 2
4 2
5 2
3 6
10 6
6 7
6 13
5 8
5 9
9 11
11 12

output

114

Note

In the first sample, the given tree has 6 vertices and it's displayed on the drawing below. Limak can jump to any vertex within distance at most 2. For example, from the vertex 5 he can jump to any of vertices: 1, 2 and 4 (well, he can also jump to the vertex 5 itself).

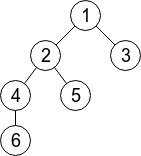
There are 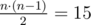 pairs of vertices (s, t) such that s < t. For 5 of those pairs Limak would need two jumps: (1, 6), (3, 4), (3, 5), (3, 6), (5, 6). For other 10 pairs one jump is enough. So, the answer is 5·2 + 10·1 = 20.

In the third sample, Limak can jump between every two vertices directly. There are 3 pairs of vertices (s < t), so the answer is 3·1 = 3.

 题意：

　　给你一棵树，求出所有f(S,T)的和;

　　f(S,T)表示，ST在树上的距离除k取上整

题解：

　　k最大只有5

　　设定DP[i][j]表示已i节点为根的子树上到i节点的距离%k=j的节点数，转移很简单

　　fs[i][j]表示已i节点为根的子树上到i节点的距离%k=j的除k的大小

　　细节需要处理好

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18+1LL;
const double Pi = acos(-1.0);
const int N = 5e5+10, M = 1e3+20, mod = 1e9+7, inf = 2e9;

vector<int > G[N];
LL dp[N][10],fs[N][10];
LL ans = 0;
int n,k,a,b;
void dfs(int u,int f) {
    dp[u][0] = 1;
    for(int i = 0; i < G[u].size(); ++i) {
        int to = G[u][i];
        if(to == f) continue;
        dfs(to,u);
        for(int j = 0; j <= k; ++j) {
            for(int h = 0; h <= k; ++h) {
                if(!dp[u][j]||!dp[to][h]) continue;
                LL tmp = j+h+1;
                if(tmp%k) tmp = tmp/k+1;
                else tmp = tmp/k;
                ans += tmp*dp[to][h]*dp[u][j]+fs[u][j]*dp[to][h]+fs[to][h]*dp[u][j];
            }
        }
        for(int j = 1; j <= k; ++j) 
            dp[u][j] += dp[to][j-1],fs[u][j] += fs[to][j-1];
        dp[u][1] += dp[to][k];fs[u][1] += fs[to][k]+dp[to][k];
    }
}
int main() {
    scanf("%d%d",&n,&k);
    for(int i = 1; i < n; ++i) {
        scanf("%d%d",&a,&b);
        G[a].push_back(b);
        G[b].push_back(a);
    }
    dfs(1,0);
    cout<<ans<<endl;
    return 0;
}