题意:
给定一个01串,一个有效的n切割定义如下:竖杠代表切割线,第一条竖杠前面的01串忽略,最后一条竖杠后面的01串忽略,将相邻竖杠夹住的01串转化成十进制数字
假设这些数字的最大值是m且这些数字囊括了1-m的所有数字,则称为一次有效切割。
问你方案数
题解:
dp[i][j] 表示以i结尾的01串中所能涵括的数状态为j的方案
那么 dp[k][j|(1<<(x-1))] += dp[i][j] (i+1 <= k <= n) x为i+1到k这串的十进制数
暴力转移统计答案
#include<bits/stdc++.h> using namespace std; #pragma comment(linker, "/STACK:102400000,102400000") #define ls i<<1 #define rs ls | 1 #define mid ((ll+rr)>>1) #define pii pair<int,int> #define MP make_pair typedef long long LL; const long long INF = 1e18+1LL; const double Pi = acos(-1.0); const int N = 75+10, M = 1e3+20, mod = 1e9+7, inf = 2e9; int dp[N][(1<<20) + 100]; int a[N],n; char s[N]; int main() { scanf("%d%s",&n,s+1); for(int i = 1; i <= n; ++i) a[i] = s[i] - '0'; for(int i = 0; i <= n; ++i) { dp[i][0] = 1; for(int j = 0; j < (1<<20); ++j) { if(dp[i][j]) { LL x = 0; for(int k = i+1; k <= n; ++k) { x += a[k]; if(x > 20) break; if(!x) continue; dp[k][j|(1<<(x-1))] += dp[i][j]; dp[k][j|(1<<(x-1))] %= mod; x *= 2; } } } } LL ans = 0; for(int i = 1; i <= n; ++i) { for(int j = 1; j <= 20; ++j) ans = (ans + dp[i][(1<<j)-1])%mod; } cout<<ans<<endl; return 0; }
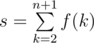 . Since the value of
. Since the value of