题目描述
小兔位于X轴的x点,欲跳至X轴的y点。x,y均为整数。小兔每次沿x轴直线跳跃,每跳的长度均为正整数,假设
小兔一共跳了n次才到目的地,每次跳的长度为F1,F2,..., Fn. 有规则如下:
F1=Fn=1
|Fi-Fi-1|<=1 , 2<=i<=n (注:| |是绝对值符号)
我们的问题是给定x,y, 如何使得n最小。
输入
包含多组数据,但不超过1000组。每组数据一行,每行包括两个整数x和y。0 <= x < y <= 1000000000 。
输出
对于每一组数据,输出一行,即从x到y的最小跳跃次数n。
样例输入
45 4845 4945 50
样例输出
334
这道题出的非常好,我一点思路也没有。
先理解清楚题意,第一步和最后一步都只能跳1,且相邻跳跃次数相差不能大于1。
我觉得画个草图能好理解点:
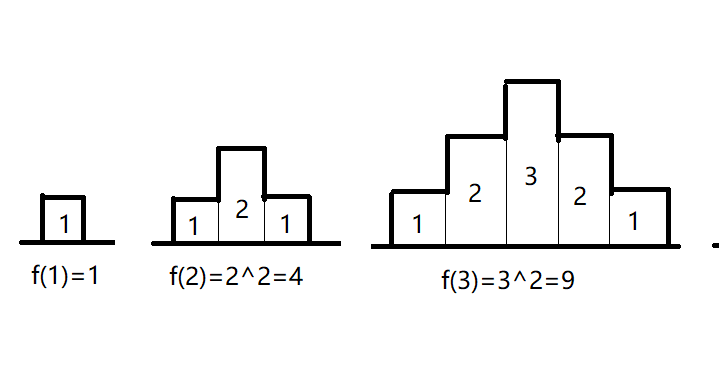
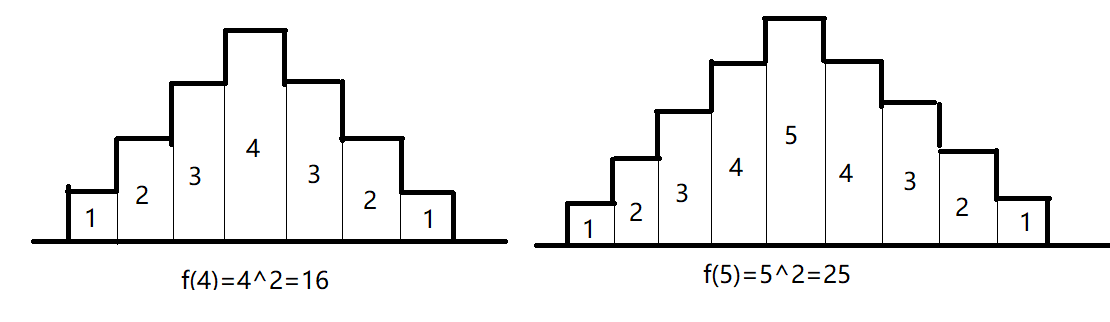
图上格子高度代表一次跳跃的长度,那么列格子数量就代表跳了几次,显然这样格子的总面积代表跳跃的距离。这样画的好处就是能很好看出第一步和最后一步只跳1。f(n)代表最高格子为按上图形式跳时的跳跃距离,其实还需要用到f(n)的递推式。
即f(n)=f(n-1)+n+n-1=f(n-1)+2n-1。而且n对应的跳跃次数为2n-1。
这样或许就好理解点了,想想看,上图是最对称最完美的跳跃方式,跳跃距离还都是平方数(感觉挺神奇的)。f(n)与f(n-1)差2n-1,也就是在f(n-1)~f(n-1)+2n-1的范围内都是n-2是最大的跳跃数。用个例子说明一下:
比如f(4)=16,f(3)=9。当距离为10时,9<10<16,易知此时“最高峰(最高的格子)“只能到3,而f(3)=9,还差1,那么好办,只需在高度为1的格子旁边再放一个高度为一的格子就能满足要求,这样也会多跳一回,所以最小跳跃次数就为(10-9)+2*3-1=6;
而当距离为15时,15-9=6>3,显然,这比“最高峰“还要大,所以一次是跳不完的,那就跳两次,也就是在高度为3的格子旁放置两个高度为3的格子。当距离再大时,最高的格子就应该为4了,问题又可以同样处理了。因此得到问题的答案:

(pos相当于上述n,len为距离)
#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<cmath> using namespace std; const int maxn=1e9+10; int a[100050]; int main() { a[1]=1; for(int i=2;;i++){ if(a[i]>maxn) break; a[i]=a[i-1]+2*i-1; } int s,t; while(scanf("%d%d",&s,&t)==2) { int len=t-s; int pos=1; for(int i=1;;i++){ if(a[i]>len&&a[i-1]<=len){ pos=i-1; break; } } len-=a[pos]; int ans=2*pos-1; if(len==0) printf("%d ",ans); else if(len<=pos) printf("%d ",ans+1); else printf("%d ",ans+2); } return 0; }