并查集

定义

并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。

并查集初始化时是一些单独的的点。如下图。

 点之间发生了关系，于是连成了线。

一条链的祖宗成为另一条链祖宗的儿子。于是链成了树。

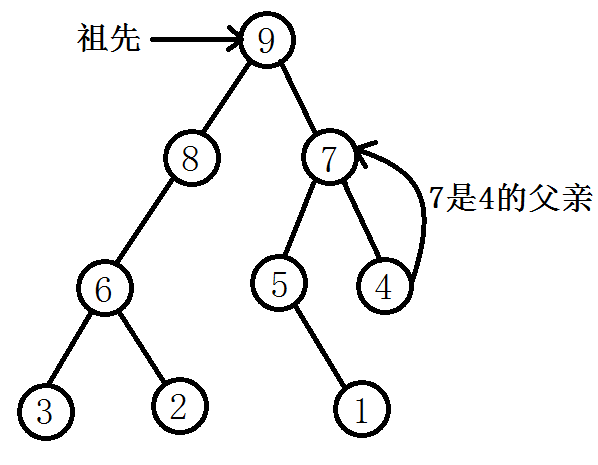
 其实并查集相当于一个庞大的家族，家族里的人有的是亲戚关系。当x脉中的任意一人与y脉中的任意一人是亲戚关系，则这两脉都是亲戚关系。

基本操作

1.初始化

首先定义一个fa数组，初始化就是令数组中每个人的爸爸都是他自己。所以f[1]暂时（这里很重要）表示1的爸爸。当出现这种情况时，它就是这一脉的祖宗。代码如下

void Initialize()
{
    for(int i=0;i<n;i++) parent[i]=i;
}

　　

2.查找

小x想知道自己的祖宗是谁，但他只知道自己的爸爸是谁。于是他问他爸爸“”你是我祖先吗？“”他的爸爸不是他祖宗，所以他爸爸问小x的爷爷，也就是他自己的爸爸说：“”你是我祖先吗？“”小x爷爷也不是，也就继续往上问。如此循环下去（假设这一脉长生不老），直到有一个人的爸爸是是他自己，也就是说他是这一脉的祖先。而用代码有两种写法，分别是递归、循环。在这里我只个人推荐递归写法。

如果我们要询问1的祖宗（假设是5）我们不得不询问2,3,4,5.这样太慢。每次查找复杂度都是O（n），太慢了！

所以此代码还有一个路径压缩，到这一步。fa数组就不表示爸爸了。为了方便询问，我们自动把f[2],f[3],f[4]都赋成5。方便后续找祖先。

int findf(int x)
{
	if(fa[x]==x) return x; //自己的爸爸是自己,返回自己的编号
	return fa[x]=findf(fa[x]); //否则询问自己的爸爸
}

 3.合并

小x和小y成为了亲戚，于是他们这两脉的成为亲戚关系。但只能有一个祖先。怎们办呢？正当他们焦头烂额的时候，我突发奇想说道：“”可以让x祖先成为y祖先的爸爸，这样不就使你们同属一个集合了吗。“”。x脉表示同意，y祖宗虽然有些不愿意。但看在我的面子上也同意了。而这就是并查集的精髓——集合合并。

void Union(int x,int y)
{
	int fx=findf(x),fy=findf(y); //fx表示x的祖宗，fy表示y的祖宗。 
	fa[fx]=fy; //令y的祖宗成为x的祖宗，这样不管是x脉还是y脉询问祖宗时都是y的祖宗。 
}

图示

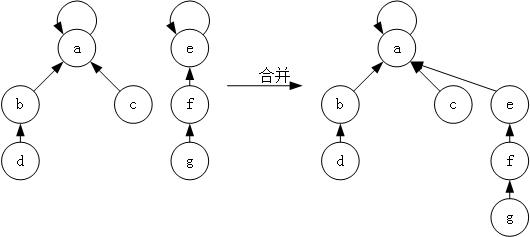
注：箭头指向自己的爸爸。

推荐

最后推荐一道模板题：洛谷P3367 【模板】并查集