【説明する】貪欲

 拉呱:

 贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　——以上来自百度百科。

* 贪心算法解题的一般步骤：
1 局部最优，当规模较小的时候做出最优的决策；
- 举例子，观察数据，大胆猜想
2 全局最优解，每一步所作的贪心选择最终能得到问题的最优解；
- 力所能及的时候，小心求证 

例题:

----------------------------------T1----------------------------------

1.洛谷  P1650 赛马+codevs  2181 田忌赛马

题目描述

我国历史上有个著名的故事： 那是在2300年以前。齐国的大将军田忌喜欢赛马。他经常和齐王赛马。他和齐王都有三匹马：常规马，上级马，超级马。一共赛三局，每局的胜者可以从负者这里取得200银币。每匹马只能用一次。齐王的马好，同等级的马，齐王的总是比田忌的要好一点。于是每次和齐王赛马，田忌总会输600银币。

田忌很沮丧，直到他遇到了著名的军师――孙膑。田忌采用了孙膑的计策之后，三场比赛下来，轻松而优雅地赢了齐王200银币。这实在是个很简单的计策。由于齐王总是先出最好的马，再出次好的，所以田忌用常规马对齐王的超级马，用自己的超级马对齐王的上级马，用自己的上级马对齐王的常规马，以两胜一负的战绩赢得200银币。实在很简单。

如果不止三匹马怎么办？这个问题很显然可以转化成一个二分图最佳匹配的问题。把田忌的马放左边，把齐王的马放右边。田忌的马A和齐王的B之间，如果田忌的马胜，则连一条权为200的边；如果平局，则连一条权为0的边；如果输，则连一条权为－200的边……如果你不会求最佳匹配，用最小费用最大流也可以啊。 然而，赛马问题是一种特殊的二分图最佳匹配的问题，上面的算法过于先进了，简直是杀鸡用牛刀。现在，就请你设计一个简单的算法解决这个问题。

输入输出格式

输入格式：

第一行一个整数n，表示他们各有几匹马（两人拥有的马的数目相同）。第二行n个整数，每个整数都代表田忌的某匹马的速度值(0 <= 速度值<= 100)。第三行n个整数，描述齐王的马的速度值。两马相遇，根据速度值的大小就可以知道哪匹马会胜出。如果速度值相同，则和局，谁也不拿钱。

【数据规模】

对于20%的数据，1<=N<=65；

对于40%的数据，1<=N<=250；

对于100%的数据，1<=N<=2000。

输出格式：

仅一行，一个整数，表示田忌最大能得到多少银币。

输入输出样例

输入样例#1：

3
92 83 71
95 87 74

输出样例#1：

200

思路：

　　贪心~    

      先分别将两个人的马按他们的速度进行排序。

　　　　那么他们的比较过程分为三种:

　　　　　　如果正序田忌的马的速度值是比齐王的快的，那么答案就对应的++，两个指针对应的向后移。

　　　　　　而如果逆序田忌马的速度是比齐王快的，答案也对应的++，两个指针对应的向前移

　　　　　　最后一种情况是如果田忌最快的马也比齐王最快的马还要慢，

　　　　　　那么就让田忌最慢的马与齐王最快的马比,并且将答案对应的--，指向田忌马的指针进行后移，指向齐王马的指针进行前移，结束。

代码酱来也~

#include <iostream>
#include <algorithm>

using namespace std;

int ans,n;
int t[2010],q[2010];
int l1,l2,r1,r2;

int main()
{
    cin>>n;
    for(int i=1; i<=n; i++) cin>>t[i]; //田忌
    for(int i=1; i<=n; i++) cin>>q[i]; //齐王

    sort(t+1,t+n+1); //从小到大进行排序 
    sort(q+1,q+n+1);
 
    l1=1,l2=1,r1=n,r2=n;
    while(l1<=r1)
    {
        if(t[l1]>q[l2]) //当前田忌最慢的马快于齐王最快的马 
        {
            l1++,l2++,ans+=200; //victory 
        }
        else
        if(t[r1]>q[r2]) //当前田忌最厉害的马快于齐王最快的马 
        {
            r1--,r2--,ans+=200; //victory 
        }
        else
        {
            if(t[l1]<q[r2]) ans-=200; //最慢的马慢于齐王最快的马 
            l1++,r2--; //defeat 
        }
    }

/* 因为最终输出的是田忌"赢取"的钱，所以不足的要输出0 */

    if(ans>0) cout<<ans;
    else cout<<"0";
    return 0;
}

---

----------------------------------T2----------------------------------

2.洛谷  P1090 合并果子+Codevs 1063 合并果子

题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有3种果子，数目依次为1，2，9。可以先将1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。

输入输出格式

输入格式：

输入文件fruit.in包括两行，第一行是一个整数n(1<＝n<=10000)，表示果子的种类数。第二行包含n个整数，用空格分隔，第i个整数ai(1<＝ai<=20000)是第i种果子的数目。

输出格式：

输出文件fruit.out包括一行，这一行只包含一个整数，也就是最小的体力耗费值。输入数据保证这个值小于2^31。

输入输出样例

输入样例#1：

3 
1 2 9 

输出样例#1：

15

说明

对于30％的数据，保证有n<=1000：

对于50％的数据，保证有n<=5000；

对于全部的数据，保证有n<=10000。

思路：

　　这个是可以用小根堆的，每次都取上面最小的两个加起来，插入堆中，每次取最小值，最后的值就为最小值，但是我不太会用……小根堆，但是是用小根堆的思想做的。

代码酱！

#include <iostream>
#include <algorithm>
#define M 12333

using namespace std;

int n,ans;
int a[M];

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+1+n);
    
    for(int i=1;i<n;i++)
    {
        ans+=a[1]+a[2];
        
        int tmp=a[1]+a[2];//记录下合并之后的数量 
        int now=n-i+1;//剩余果子数目 
        int cnt=0,j;//cnt用来计数 
        
        for(j=3;j<=now&&a[j]<tmp;j++) a[++cnt]=a[j];//找出比合并之后小的 
        a[++cnt]=tmp;//重新进行排序 
        for(;j<=now;j++) a[++cnt]=a[j];//将剩余的进行更新 
    }
    
    cout<<ans;
    
    return 0;
}

---

----------------------------------T3----------------------------------

3.活动安排问题(未经检验……)

题目描述：

有 N 场活动，每场活动在特定的时间需要占用场地。
如果有两场活动需要同一时间占用场地，则不能同时举行
问最多能举行多少场活动？

代码酱来也~

#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 1e5 + 6;

struct activity
{
    int start, end;
    bool operator < (const activity &qwq) const
    {
        return end < qwq.end;
    }
}a[N];

int n;

int main()
{
    scanf("%d", &n);
    for(int i=1; i<=n; i++) 
        scanf("%d%d", &a[i].start, &a[i].end);

    sort(a+1, a+n+1);

    int cur = 0, ans = 0;

    for(int i=1; i<=n; i++)
        if(a[i].start > cur) cur = a[i].end, ++ans;
/* cur用来记录当前活动进行到何处，因为至少是从0开始进行，所以如果活动是在cur之前开始进行，那么它将不能够被选上，又因为是按照结束时间进行排的序，所以第一个出现的能够被安排上就将她安排上就行，以此类推，直到最后，如果活动结束在规定范围之外，也不被选入，什么的…… */

    printf("%d
", ans);//输出结果

    return 0;
}

---

----------------------------------T4----------------------------------

4.洛谷  P1809 过河问题_NOI导刊2011提高（01）

题目描述

有一个大晴天，Oliver与同学们一共N人出游，他们走到一条河的东岸边，想要过河到西岸。而东岸边有一条小船。 

船太小了，一次只能乘坐两人。每个人都有一个渡河时间T，船划到对岸的时间等于船上渡河时间较长的人所用时间。 

现在已知N个人的渡河时间T，Oliver想要你告诉他，他们最少要花费多少时间，才能使所有人都过河。 

注意，只有船在东岸（西岸）的人才能坐上船划到对岸。

输入输出格式

输入格式：

输入文件第一行为人数N，以下有N行，每行一个数。 

第i+1行的数为第i个人的渡河时间。

输出格式：

输出文件仅包含一个数，表示所有人都渡过河的最少渡河时间

输入输出样例

输入样例#1：

4 
6 
7 
10 
15 

输出样例#1：

42

说明

[数据范围] 

对于40%的数据满足N≤8。 

对于100%的数据满足N≤100000。

[样例解释] 

初始：东岸{1，2，3，4}，西岸{} 

第一次：东岸{3，4}，西岸{1，2} 时间7 第二次：东岸{1，3，4}，西岸{2} 时间6 第三次：东岸{1}，西岸{2，3，4}，时间15 第四次：东岸{1，2}，西岸{3，4} 时间7 第五次：东岸{}，西岸{1，2，3，4} 时间7 

所以总时间为7+6+15+7+7=42，没有比这个更优的方案。

思路：

      方法有两种，第一种是让第一第二快的当运的，首先让第一快和第一慢快的一起过去，然后让最快的来回接送其他人(先接慢的)，这样貌似是最优的。

但是这样考虑并不够完全，还有一种情况，就是第一快和第二快先划过去，让第一快回来，但先暂时不让它回去，让第一慢和第二慢回去，再让第二快回来，

(他们两种做法都仅仅只能够送2个人到达对岸)

在某些比较特殊的情况下这种情况是比第一种快的，所以我们应该在两者之间取花费时间更加小的。

还有就是需要在只有1个，2个，3个人时，分别特判一下。

代码酱来也~

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#define LL long long//不开也可以啦,我闲的慌而已 

using namespace std;

const int M = 100010;

int n;
LL t[M];

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        cin>>t[i];
    }
    sort(t+1,t+1+n);

    int shengyu=n;
    LL ans=0;
    while(shengyu)
    {
        if(shengyu == 1)
        {//1自己过河 
            ans+=t[1];
            break;
        }
        if(shengyu == 2)
        {//1,2过河 
            ans+=t[2];
            break;
        }
        if(shengyu == 3)
        {//1,3过河，1回，1,2过河 
            ans+=t[3]+t[1]+t[2];
            break; 
        }
        else
        {
            ans+=min(t[2]+t[1]+t[shengyu]+t[2],//1,2过河,1回,最慢的两个过河,2回 
            t[shengyu]+t[1]+t[shengyu-1]+t[1]);//1,第一慢过河,1回,1跟第二慢过河,1回
            shengyu-=2;//成功的运载了两人 
        }
    }
    cout<<ans;
    return 0;
}

---

----------------------------------T5----------------------------------

5.洛谷 P1325 雷达安装+codevs 2625 雷达安装

题目描述

描述：

假设海岸线是一条无限延伸的直线。它的一侧是陆地，另一侧是海洋。每一座小岛是在海面上的一个点。雷达必须安装在陆地上（包括海岸线），并且每个雷达都有相同的扫描范围d。你的任务是建立尽量少的雷达站，使所有小岛都在扫描范围之内。

数据使用笛卡尔坐标系，定义海岸线为x轴。在x轴上方为海洋，下方为陆地。

样例1如图所示

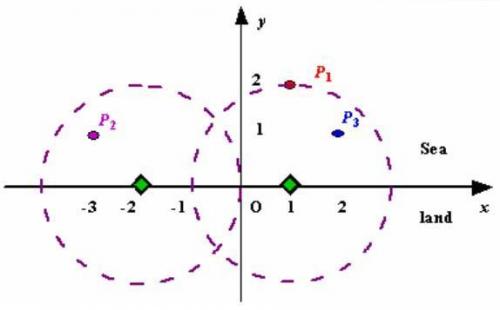
输入输出格式

输入格式：

第一行包括2个整数n和d，n是岛屿数目，d是雷达扫描范围。

接下来n行为岛屿坐标。

输出格式：

一个整数表示最少需要的雷达数目，若不可能覆盖所有岛屿，输出“-1”。

输入输出样例

输入样例#1：

3 2
1 2
-3 1
2 1

输出样例#1：

2

思路：

　　我们可以将问题稍微进行转化：将基站设为覆盖半径为 d。
则问题变为：每个基站的覆盖区域必须要有雷达这样一个问题。

　　又因为雷达只能放在 X 轴上，所以每个基站覆盖的其实是一条线段。
则问题又变为：每条线段上必须要要有雷达。

那么这个看似十分难理解的题目就简单地转化为活动安排问题！~

代码酱来也~

#include <iostream>
#include <cmath>
#include <cstdio>
#include <algorithm>
#include <string>
#include <cstring>
#define M 100001

using namespace std;

struct q{
    int x,y;
}dao[M];

struct qq{
    float s,e;
    bool operator < (const qq &qwq) const//重载运算符
    {
        return e < qwq.e;
    }
}biao[M];

bool v[M];
int n,d,ans;
int maxy=0;

int main()
{
    scanf("%d%d",&n,&d);
    for(int i=1;i<=n;i++)
    {
        cin>>dao[i].x>>dao[i].y;
        if(dao[i].y>maxy) maxy=dao[i].y;
        /*
        if(dao[i].y>d)
        {
            cout<<"-1";//这样写也是可以的
            return 0;    
        }
        */
    }
    if(maxy>d)
    {
        cout<<"-1";
        return 0;
    }
    float qqq;
    for(int i=1;i<=n;i++)
    {
        qqq=sqrt(1.0*d*d-dao[i].y*dao[i].y);//勾股定理 
        biao[i].s=dao[i].x-qqq;//转换为线段
        biao[i].e=dao[i].x+qqq;
    }
    sort(biao+1,biao+1+n);
    for(int i=1;i<=n;i++)
    {
        if(!v[i])
        {
            v[i]=1;//此处必须进行标记！
            for(int j=1;j<=n;j++)
            {
                if(!v[j]&&biao[j].s<=biao[i].e)
                {
                    v[j]=1;
                }
            }
            ans++;
/*因为所有在这个范围之内的都能够用1个雷达覆盖，所以仅仅需要将雷达个数+1即可*/
        }
         
    }
    cout<<ans;
    return 0;
}