题意翻译
给你一串数列a.对于一个质数p,定义函数f(p)=a数列中能被p整除的数的个数.给出m组询问l,r,询问[l,r]区间内所有素数p的f(p)之和.
题目描述
Recently, the bear started studying data structures and faced the following problem.
You are given a sequence of integers x1,x2,...,xn x_{1},x_{2},...,x_{n} x1,x2,...,xn of length n n n and m m m queries, each of them is characterized by two integers li,ri l_{i},r_{i} li,ri . Let's introduce f(p) f(p) f(p) to represent the number of such indexes k k k , that xk x_{k} xk is divisible by p p p . The answer to the query li,ri l_{i},r_{i} li,ri is the sum: 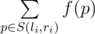 , where S(li,ri) S(l_{i},r_{i}) S(li,ri) is a set of prime numbers from segment [li,ri] [l_{i},r_{i}] [li,ri] (both borders are included in the segment).
, where S(li,ri) S(l_{i},r_{i}) S(li,ri) is a set of prime numbers from segment [li,ri] [l_{i},r_{i}] [li,ri] (both borders are included in the segment).
Help the bear cope with the problem.
输入输出格式
输入格式:
The first line contains integer n n n (1<=n<=106) (1<=n<=10^{6}) (1<=n<=106) . The second line contains n n n integers x1,x2,...,xn x_{1},x_{2},...,x_{n} x1,x2,...,xn (2<=xi<=107) (2<=x_{i}<=10^{7}) (2<=xi<=107) . The numbers are not necessarily distinct.
The third line contains integer m m m (1<=m<=50000) (1<=m<=50000) (1<=m<=50000) . Each of the following m m m lines contains a pair of space-separated integers, li l_{i} li and ri r_{i} ri (2<=li<=ri<=2⋅109) (2<=l_{i}<=r_{i}<=2·10^{9}) (2<=li<=ri<=2⋅109) — the numbers that characterize the current query.
输出格式:
Print m m m integers — the answers to the queries on the order the queries appear in the input.
输入输出样例
7 2 3 5 7 11 4 8 2 8 10 2 123
0 7
首先可以线性筛筛出 1e7 里面所有的素数;
对于每一个x[i] ,我们记录其次数,然后类似于埃筛的做法,对于每个素数,用 sum [ i ] 来累计有该素数因子的数的个数;
最后用前缀和维护;
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 10000005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
ll x = 0;
char c = getchar();
bool f = false;
while (!isdigit(c)) {
if (c == '-') f = true;
c = getchar();
}
while (isdigit(c)) {
x = (x << 1) + (x << 3) + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
ll gcd(ll a, ll b) {
return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }
/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
if (!b) {
x = 1; y = 0; return a;
}
ans = exgcd(b, a%b, x, y);
ll t = x; x = y; y = t - a / b * y;
return ans;
}
*/
ll qpow(ll a, ll b, ll c) {
ll ans = 1;
a = a % c;
while (b) {
if (b % 2)ans = ans * a%c;
b /= 2; a = a * a%c;
}
return ans;
}
int n;
int x[maxn];
int m;
int cnt[maxn];
int prime[maxn];
int tot = 0;
int sum[maxn];
bool vis[maxn];
void init() {
vis[1] = 1;
for (int i = 2; i < maxn; i++) {
if (!vis[i])prime[++tot] = i;
for (int j = 1; prime[j] * i < maxn; j++) {
vis[prime[j] * i] = 1;
if (i%prime[j] == 0)break;
}
}
}
int main()
{
//ios::sync_with_stdio(0);
rdint(n);
for (int i = 1; i <= n; i++)rdint(x[i]), cnt[x[i]]++;
init();
for (int i = 1; i <= tot; i++) {
for (int j = 1; j*prime[i] < maxn; j++) {
sum[i] += cnt[j*prime[i]];
}
}
for (int i = 1; i <= tot; i++)sum[i] += sum[i - 1];
rdint(m);
while (m--) {
int l, r; rdint(l); rdint(r);
int pos1 = upper_bound(prime + 1, prime + 1 + tot, r) - prime - 1;
int pos2 = lower_bound(prime + 1, prime + 1 + tot, l) - prime - 1;
// cout << pos1 << ' ' << pos2 << endl;
cout << sum[pos1] - sum[pos2] << endl;
}
return 0;
}