入门平衡树: Treap

入门平衡树：(treap)

前言：

• 如有任何错误和其他问题，请联系我
  • 微信/QQ同号：615863087

前置知识：

• 二叉树基础知识，即简单的图论知识。

初识(BST)：

• (BST)是((Binary::Search::Tree))的简写，中文名二叉搜索树。
• 想要了解平衡树，我们就先要了解这样一个基础的数据结构: 二叉搜索树。
• 所以接下来会先大篇幅讨论(BST)
• 了解了(BST)后，(Treap)也就顺理成章了。
• 二叉树有两类非常重要的性质：
  • 1：堆性质
    • 堆性质又分为大根堆性质和小根堆性质。小根堆的根节点小于左右孩子，且这是一个递归定义。对于大根堆则是大于。(c++)提供的(priorioty\_queue)就是一个大根堆。
  • 2：(BST)性质
    • 给定一棵二叉树，树上的每个节点都带有一个数值，成为节点的“关键吗”。对于树中任意一个节点满足(BST)性质，指:
      • 该节点的关键码不小于他左子树的任意节点的关键码。
      • 该节点的关键码不大于他右子树的任意节点的关键码。
• 举个拓展的例子，笛卡尔树既满足堆性质，又满足(BST)性质。

  • 笛卡尔树并不常见，博主也只见过几次，也偶尔成功地用别的数据结构(AC)掉对应的题目，是下来后看题解才发现可以用笛卡尔树写。

  • 似乎可以用单调栈替代？希望了解的奆奆可以联系我或者评论区告诉我。

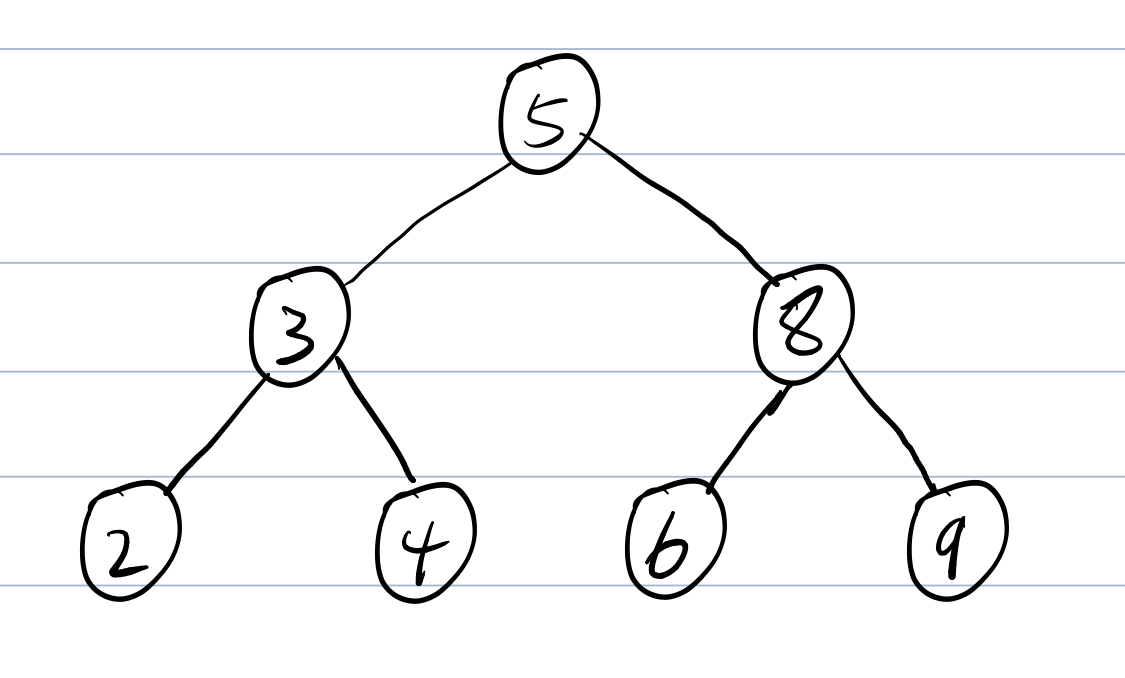
  • 这里给出一张笛卡尔树的图片帮助大家了解(BST)性质和堆性质，不多做介绍。

  • 

  • (图源:维基百科)

  • 笛卡尔树中的(index)满足(BST)性质，(value)满足堆性质。

    • 其中(index)是图中蓝色框出现的顺序，(val)是蓝色框出现的权值。
    • 很显然这棵树满足小根堆性质，也满足(BST)性质。
• 那么我们接下来介绍的二叉搜索树就是一棵满足(BST)性质的二叉树，可以结合此图加深理解。
• 

(BST)的相关操作：

(BST)的建立:

• 为了避免数组越界同时减少特判，我们一般在(BST)中插入两个额外的节点，其中两个节点的权值其中一个为(+INF)，另一个为(-INF)。
• 不明白为什么能够减少特判可以先往下阅读。

const int INF = 0x3f3f3f3f;
int tot, root, n;
struct Treap //入门级平衡树
{
    int l, r;  //左右子节点在数组中的下标
    int val;  //节点权值
}a[maxn];

int New(int val)
{
    a[++tot].val = val;
    return tot;
}

void Build()
{
    New(-INF), New(INF);
    root = 1; a[1].r = 2;
}

(BST)的检索:

• 为了方便，我们假设树中没有相同权值的节点。
• 在(BST)中检索关键码为(val)的节点。根据(BST)性质，我们可以：
  • 当(val)等于当前节点的关键码
    • 说明找到了这个节点
  • 当(val)小于当前节点的关键码
    • 若当前节点左子树为空，则说明不存在(val)。
    • 否则递归进入左子树。
  • 当(val)大于当前节点的关键码
    • 若当前节点右子树为空，则说明不存在(val)。
    • 否则递归进入右子树

int Get(int &p, int val)
{
    if(p == 0) 
    {
        p = New(val);
        return;
    }
    if(val == a[p].val) return p;
    return val < a[p].val ? Get(a[p].l, val) : Get(a[p].r, val);
}

(BST)的插入：

• 为了方便，我们假设即将插入的点的权值在树中不存在。
• 与检索过程类似，当发现要走向的子节点为空的时候，直接建立关键码为(val)的新节点为(p)的子节点。

void ins(int &p, int val)
{
    if(p == 0)
    {
        p = New(val);
        return;
    }
    if(val == a[p].val) return;
    if(val < a[p].val) ins(a[p].l, val);
    else ins(a[p].r, val);
}

(BST)求前驱/后继:

• (val)的前驱指小于(val)且最大的数，(val)的后继指大于(val)且最小的数。

• 求后继：

  • 初始化(ans)为具有正无穷关键码的那个节点的编号。然后在(BST)中检索(val)。在检索过程中，每经过一个节点，都检查节点的关键码，判断能否更新所求的后继。
  • 检索完成有三种可能：
  • (1:) 没有找到(val)，此时(val)的后继就在已经经过的节点中。此时(ans)为所求。
  • (2:) 找到了关键码为(val)的节点(p)，但(p)没有右子树。那么此时的(ans)为所求。
  • (3:) 找到了关键码为(val)的节点(p)，且(p)有右子树，那么就从(p)的右孩子出发一直向左走，就找到了(val)的后继。

  int GetNext(int val)
  {
      int ans = 2; // a[2].val = INF
      int p = root;
      while(p)
      {
          if(val == a[p].val)
          {
              if(a[p].r > 0)
              {
                  p = a[p].r;
                  while(a[p].l > 0) p = a[p].l;
                  ans = p;
              }
              break;
          }
          if(a[p].val >val && a[p].val < a[ans].val) ans = p;
          p = val < a[p].val ? a[p].l : a[p].r;
      }
      return a[ans].val;
  }
  

(BST)的节点删除：

• 从(BST)中删除节点权值为(val)的数字。
• 首先检索得到权值为(val)的节点(p)。
• 节点(p)的子节点数目小于(2)，则直接删除该节点，并让子节点代替(p)的位置。
• 若(p)节点又有左子树又有右子树，则求出(p)的后继节点(next)。根据我们上面的分析，后继是进入右子树后一直往左走，那么这个后继节点(next)是不会有左子树的。这一点可以用反证法简单的证明一下。
  • 如果此时的(next)节点有左子树，此时再来看后继的定义：大于(val)的最小数，那么此时(next)再往左走能得到大于(val)的且比(next)节点权值更小的一个数，即(next)不为(p)的后继节点。矛盾。
• 此时我们直接删除节点(next)(删除之前要记录一下)，再用(next)的右子树代替节点(next)的位置，再删除(p)，再用记录下来的(next)代替(p)的位置。

其他：

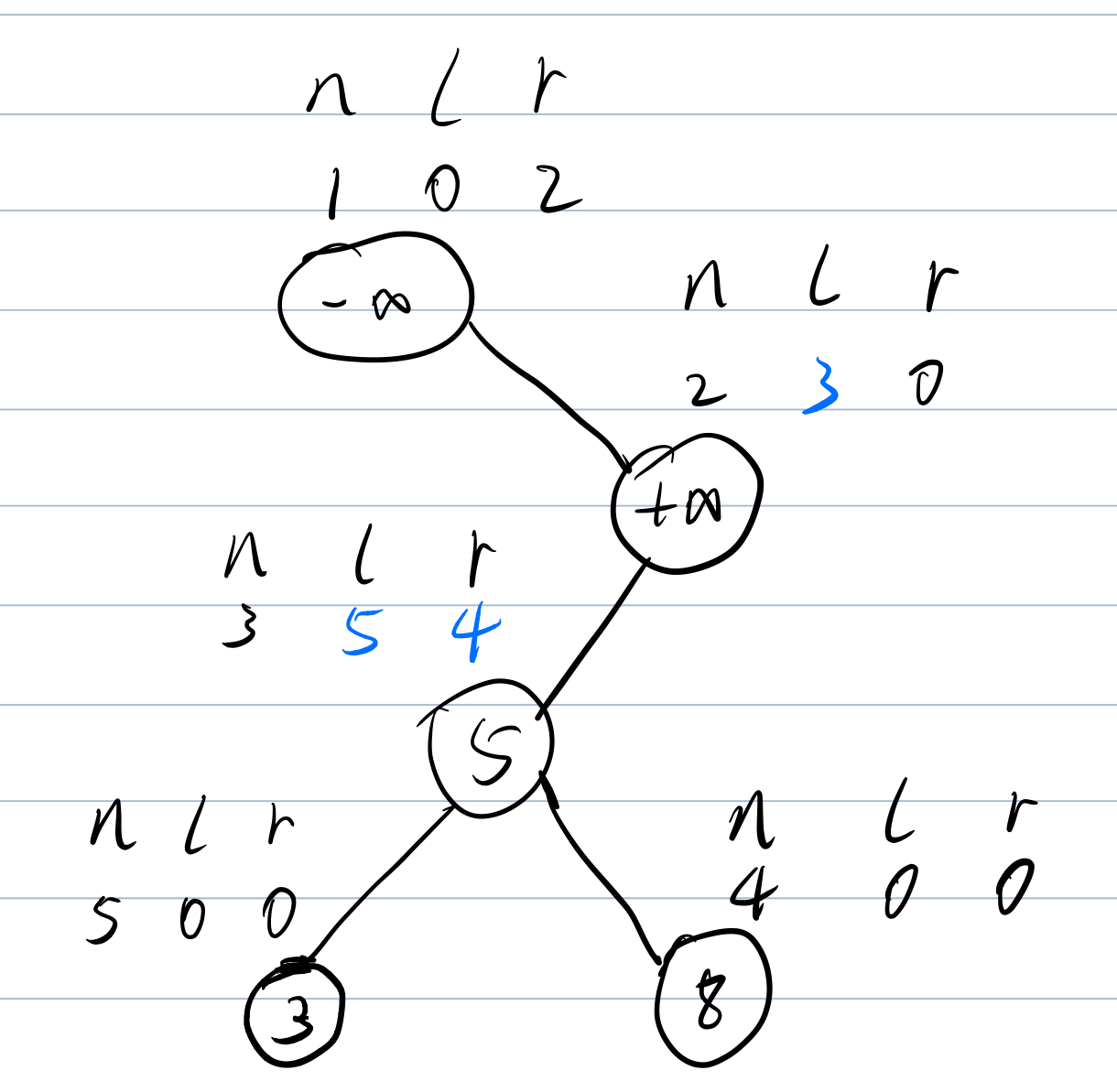
• 来解决一下为什么插入两个特殊的节点能减少特判的原因。

• 在主观上，我们去画图模拟这样一棵(BST)，有没有这两个节点是无所谓的。但是到了代码实现里，插入这两个节点却极大的方便了我们代码的编写。

• 手动模拟插入几个节点试试看会是什么样：

• 

• 这样的话十分清楚了，如果我们插入的时候还没有节点我们也可以直接插入，检索前驱后继也可以分别从一号或者二号节点开始，即使删除操作把点全部删光了依然会有两个节点在那。我们每次操作只需要关注我们想做的事，不需要关注什么乱七八糟的有没有节点啊，树是不是空的啊，查找前驱我应该从哪里开始啊等等等等的问题，就能完完全全根据伪代码写。(话糙理不糙)【划掉。

(BST)复杂度分析

(BST)时间复杂度分析：

• 一棵(N)个节点的二叉树深度一般为(logN)，所以他也能保证每一次操作的复杂度为(O(logN))。
• 但是当遇到插入一个有序序列的情况，那么(BST)将退化成一条链，操作的复杂度也将退化为(O(n))。
• 为了解决这个问题，保证(BST)的平衡，产生了各种平衡树如(AVL)树，红黑树，替罪羊树等。
  • (这三个除了红黑树以外我都没了解过(QwQ))
• 其中入门级别的平衡树是(Treap)，较为常用的是(Splay)。本着入门的精神，接下来我们来看看(Treap)。

(Treap)

旋转操作：

• 对于一个序列(1,2,3,4,5)，或者乱序成(2,3,1,5,4)。将它们插入(BST)中，得到的(BST)其实是等价的。但是第一种显然在复杂度上不占优。

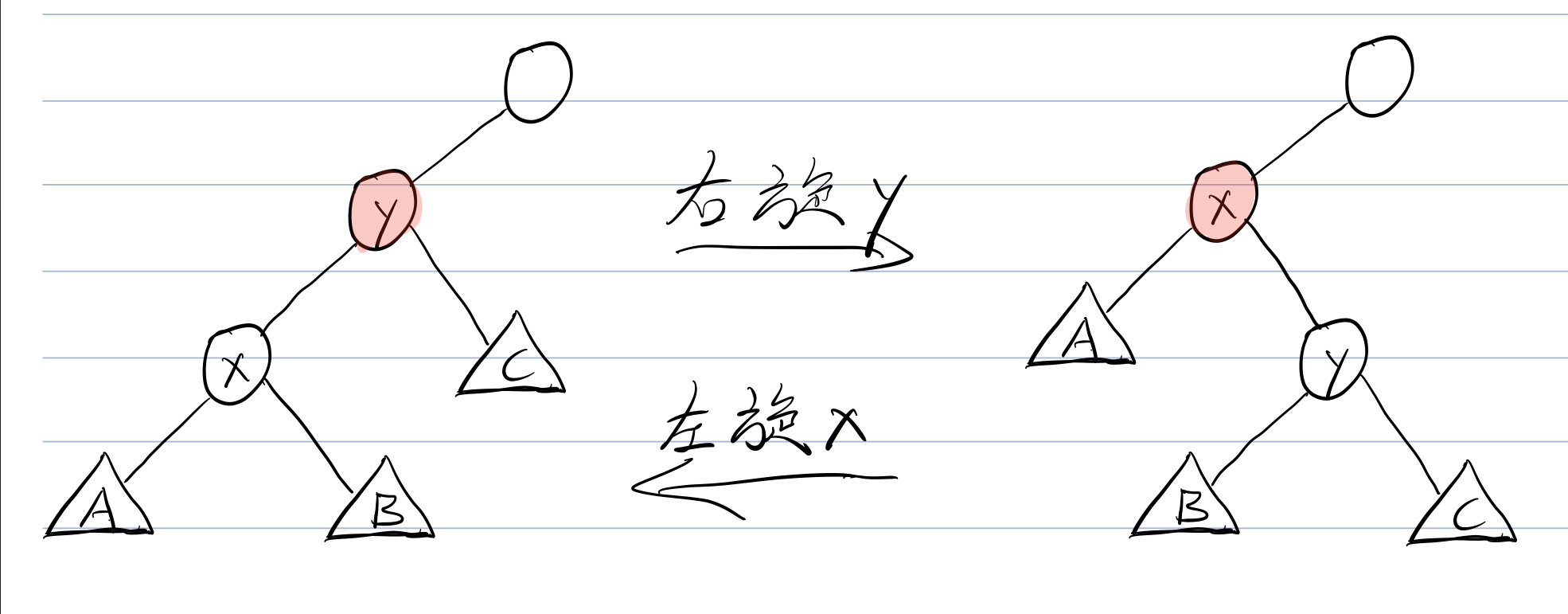
• 我们将通过变形来更改(BST)的形态但同时让他保持原来的信息这样的操作，叫做"旋转"。旋转又分为左旋和右旋。

• 可以结合此图加深理解

• 

• 即我们可以通过旋转来将原本退化的(BST)通过等价变换成为一棵能保证复杂度的树。

什么样旋转是合理的？

• 在随机数据下，一棵(BST)就是平衡的。所以(treap)的思想就是利用随机来创造平衡条件。
• (treap)是(tree)和(heap)的结合。所以(treap)有两个关键字，一个是随机附上的数值，一个是原本的权值。
• 当我们插入一个新结点的时候，我们对其附上一个随机值，然后像二叉堆那样进行左旋或者右旋来进行调整，这样既能保证平衡性又能保证(BST)性质。
  • 好像有点靠脸(AC)的意思？【划掉
  • 但只要没有被大佬(\%)而导致(rp-=INF)问题应该也不大。
  • (Splay)是一个不错的选择，更通用，也不会因为随机建值靠脸拿分。

模板题:

Acwing255: 普通平衡树

洛谷3369: 普通平衡树

• 两个地址提供的是一道题，但建议两个地方都交一下。

• 代码模板源于蓝书，详细注释

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;
const int INF = 0x3f3f3f3f;

int tot, root, n;
struct Treap
{
    int l, r;  //左右子节点
    int val, dat; //Bst的权值 堆的权值 满足大根堆性质
    int cnt, sz;  //重复的数量 子树(包括根节点)的大小
}a[maxn];

//新建一个节点
int New(int val)
{
    a[++tot].val = val;
    a[tot].dat = rand(); //给堆的那一部分附上随机值
    a[tot].cnt = a[tot].sz = 1; //此时重复数和子树都为1
    return tot;
}

void update(int p){ //更新当前父节点的信息
    a[p].sz = a[a[p].l].sz + a[a[p].r].sz + a[p].cnt;
}

//初始建立treap 其中有两个特殊节点
void Build()
{
    New(-INF), New(INF);
    root = 1; a[1].r = 2;
    update(root); //更新根节点
}

int GetRankByVal(int p, int val)
{
    if(p == 0) return 0; //如果没有这个节点
    //如果此时找到了 那么排名就为小于他的数字+自身
    if(val == a[p].val) return a[a[p].l].sz + 1;
    //可以直接向左走
    if(val < a[p].val) return GetRankByVal(a[p].l, val);
    //向右走的话其实就相当于左半部分加上根全部小于他
    return GetRankByVal(a[p].r, val) + a[a[p].l].sz + a[p].cnt;
}

//查找排名为rk的数
int GetValByRank(int p, int rk)
{
    if(p == 0) return INF; //空节点
    //如果当前节点左子树的规模大于rk
    //那么说明答案一定在左子树中
    if(a[a[p].l].sz >= rk)
        return GetValByRank(a[p].l, rk);
    if(a[a[p].l].sz + a[p].cnt >= rk)
        return a[p].val;
    //向右走的时候rk要减去左子树和根节点的规模
    return GetValByRank(a[p].r, rk - a[a[p].l].sz - a[p].cnt);
}

void zig(int &p) //右旋操作
{
    int q = a[p].l;  //左子树
    a[p].l = a[q].r; //左子树的右子树拼接到根节点的左子树上
    a[q].r = p; //左子树的右子树变为根节点 左子树的左子树不变
    p = q;   //把原来左子树的信息换过去
    update(a[p].r); update(p);//例行更新两个父节点的信息
}

void zag(int &p) //左旋操作 同理与右旋
{
    int q = a[p].r; 
    a[p].r = a[q].l; a[q].l = p; p = q;
    update(a[p].l); update(p);
}

//插入和删除操作 一般会涉及到旋转
//所以这时候采用递归写法 以便于更新节点信息
void ins(int &p, int val)
{
    if(p == 0)
    { 
        p = New(val);
        return;
    }
    if(val == a[p].val)
    {
        a[p].cnt++; update(p);
        return;
    }
    if(val < a[p].val)
    {
        ins(a[p].l, val); //因为需要满足大根堆性质
        //当我的左子节点的堆权值大于根节点的时候
        //右旋把左子节点换上来
        if(a[p].dat < a[a[p].l].dat) zig(p);
    }
    else
    {
        ins(a[p].r, val);
        if(a[p].dat < a[a[p].r].dat) zag(p);
    }
    update(p);
}

//找到需要删除的节点并将其下旋至叶子节点后删除
//减少维护节点信息等复杂问题
void del(int &p, int val)
{
    if(p == 0) return;
    if(val == a[p].val)//检测到了val
    {
        if(a[p].cnt > 1)
        {
            a[p].cnt--, update(p); //直接减掉一个副本即可
            return; //退出
        }
        if(a[p].l || a[p].r)//不是叶子节点 向下旋转
        {
            if(a[p].r == 0 || a[a[p].l].dat > a[a[p].r].dat)
            {zig(p); del(a[p].r, val);} //右旋 后进入右子树
            else {zag(p); del(a[p].l, val);}
            update(p);//例行更新父节点信息
        }
        else p = 0;  //是叶子节点 直接删除
        return;
    }
    val < a[p].val ? del(a[p].l, val) : del(a[p].r, val);
    update(p);
}

int GetPre(int val)
{   //前驱:小于x且最大的数
    int ans = 1; //a[1].val = -INF
    int p = root; 
    while(p)
    {
        if(val == a[p].val) //找到了节点值相同的
        {    
            if(a[p].l > 0)  //如果有左子树
            {
                p = a[p].l; //不停向右走
                while(a[p].r > 0) p = a[p].r; 
                ans = p;
            }
            break;  //此时的ans为答案
        }
        //就算找不到val 前驱也被ans经过了
        if(a[p].val < val && a[p].val > a[ans].val) ans = p;
        p = val < a[p].val ? a[p].l : a[p].r; 
    }
    return a[ans].val;
}

int GetNext(int val)
{   //后继:大于x且最小的数
    int ans = 2; // a[2].val = INF
    int p = root;
    while(p)
    {
        if(val == a[p].val)
        {
            if(a[p].r > 0)
            {
                p = a[p].r;
                while(a[p].l > 0) p = a[p].l;
                ans = p;
            }
            break;
        }
        if(a[p].val >val && a[p].val < a[ans].val) ans = p;
        p = val < a[p].val ? a[p].l : a[p].r;
    }
    return a[ans].val;
}

int main()
{
    Build();
    scanf("%d", &n);
    int op, x;
    while(n--)
    {
        scanf("%d%d", &op, &x);
        if(op == 1)
        {//插入x数
            ins(root, x);
        }
        if(op == 2)
        {//删除x(若有多个x,只删除一个)
            del(root, x);
        }
        if(op == 3)
        {//查询x的排名(排名定义为比当前数小的个数+1)
         //若有多个相同的数 输出最小的排名
            printf("%d
", GetRankByVal(root, x) - 1);
        }
        if(op == 4)
        {//查询排名为x的数
            printf("%d
", GetValByRank(root, x + 1));
        }
        if(op == 5)
        {//求x的前驱(小于x且最大的数)
            printf("%d
", GetPre(x));
        }
        if(op == 6)
        {//求x的后继(大于x且最小的数)
            printf("%d
", GetNext(x));
        }
    }
    return 0;
}