主席树学习笔记

主席树学习笔记

参考博文

• https://blog.csdn.net/bestFy/article/details/78650360

前置知识

• 权值线段树
• 权值线段树和普通线段树区别在于他们维护的东西不一样：
  • 权值线段树维护值域，普通线段树维护区间。

初始主席树

• 主席树的发明人的名字简称是(hjt)，所以得名主席树。

• 主席树全称是可持久化权值线段树。

• 可持久化思想可以观察此图来理解：

• 

• 图中红色的为历史节点，蓝色的是新建节点(修改后的节点)。

• 每次只更改一条链，也就是(logn)个点。

• 主席树不采用(p*2,p*2+1)的方式来表示左右儿子，而是需要动态开点地保存左右儿子的编号，从而节约空间。

经典入门问题

• 洛谷3834：主席树模板
• 给定一个序列长度为(n)，给定(m)个询问，每次询问指定的闭区间([L,R])内查找区间内第(k)小值。
• 数据范围(1leq n,mleq 2*10^5,-10^9leq a_ileq 10^9)。

问题分析

• 首先考虑从区间([1,n])查询区间第(k)小要怎么做，这里很明显，可以使用权值线段树来做。

• 这里给一道例题在这。链接。

• 那接下来考虑这个问题，先简化一下问题，求区间([1,R])第(k)小的数字要怎么做？

• 首先找到插入(R)节点时的历史版本，然后用普通权值线段树就可以了。

• 那么现在拓展到原问题，求([L,R])区间的第(k)小值。

• 这里需要运用前缀和的知识。对于求([L,R])的值，我们只需要用([1,R])的信息减去([1,L-1])的信息。

• 模拟一下这个过程：

• 假设序列长度为(4)，序列为(3 1 2 4)，查询([2,3])区间第(2)小的数字。

• 插入(3)

• 

• 插入(1)

• 

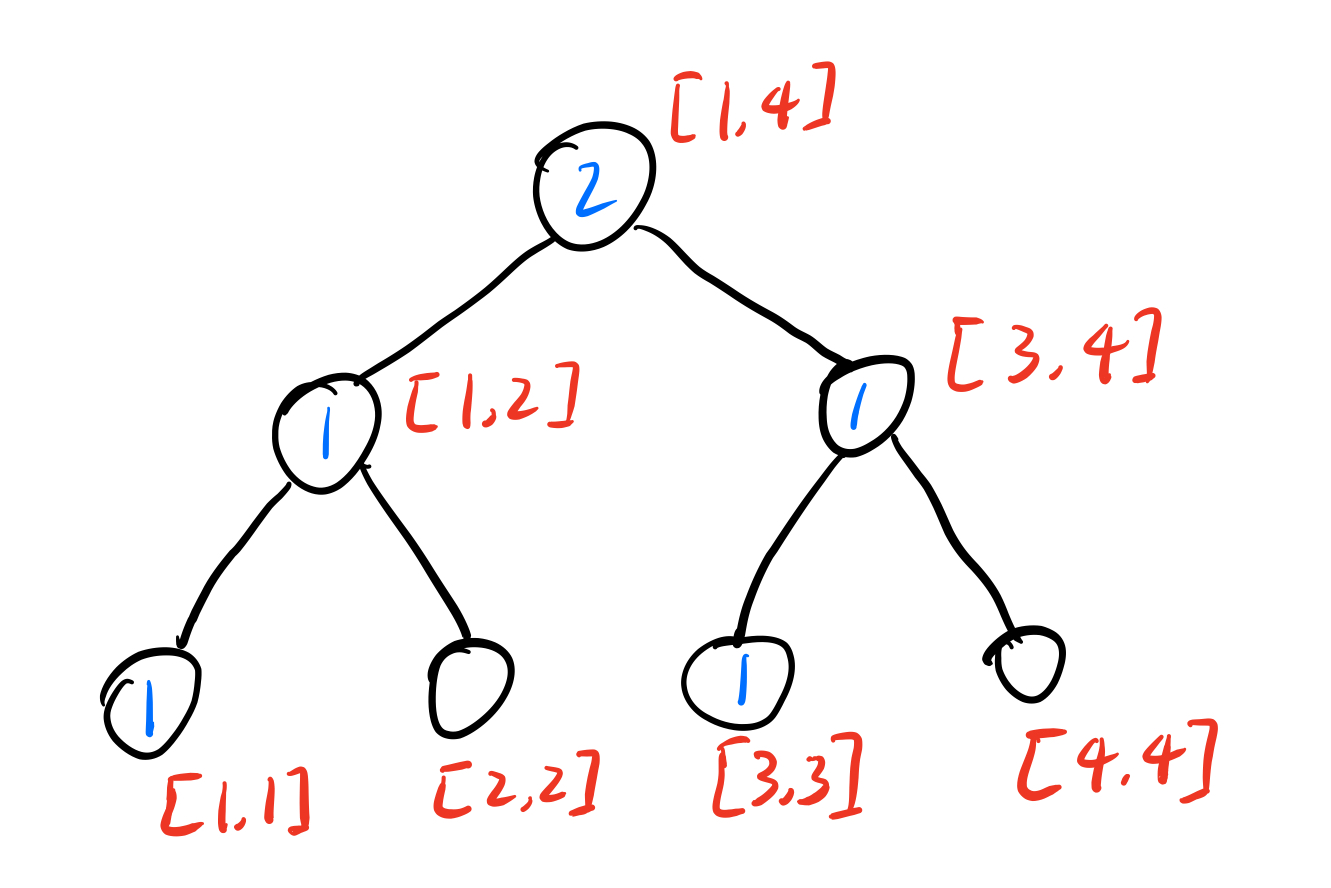
• 插入(2)

• 

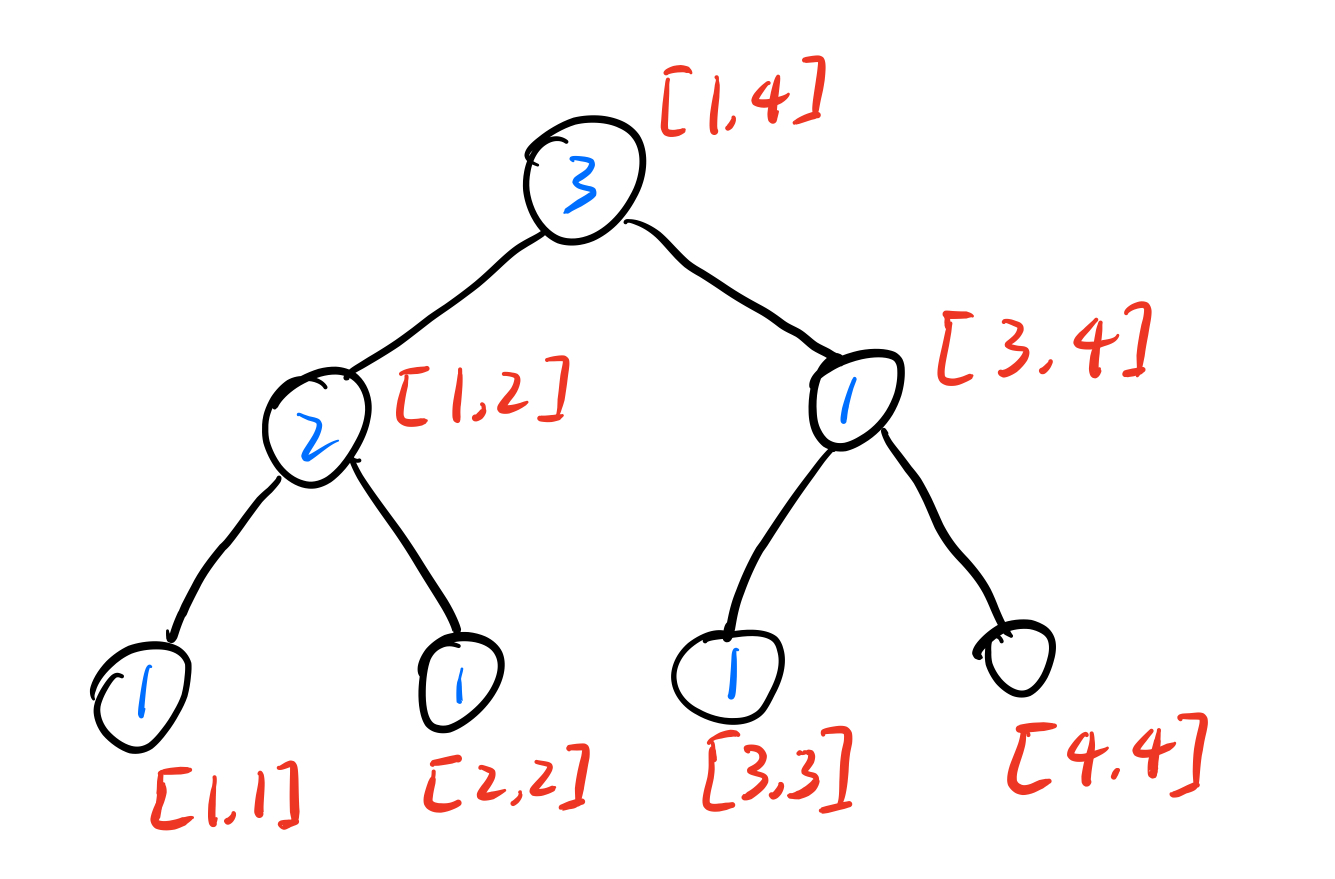
• 插入(4)

• 

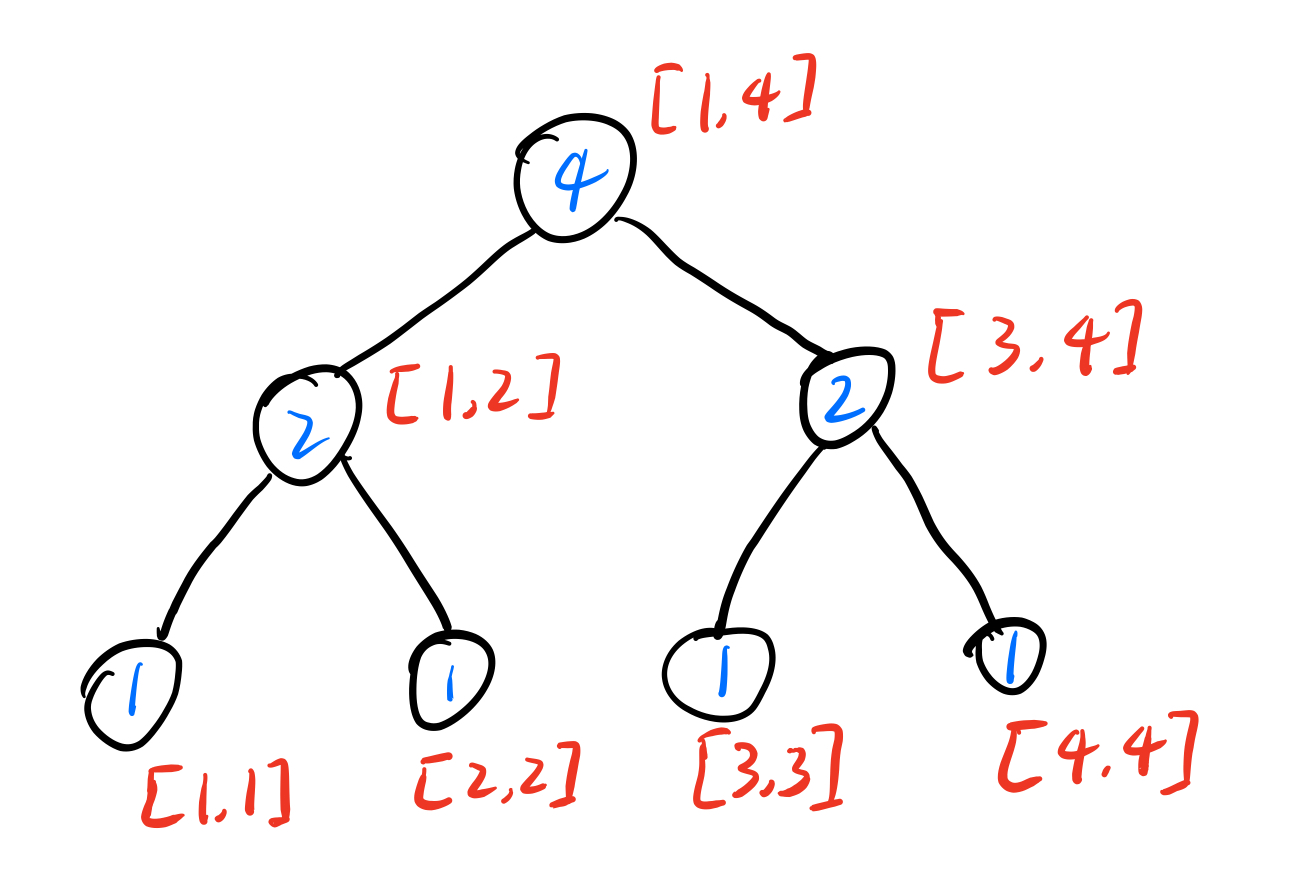
• 序列为(3 1 2 4)。

• 我们现在要查询([2,3])区间内第(2)小的数字，首先需要把第(1)棵线段树和第(3)棵线段树拿出来

• 

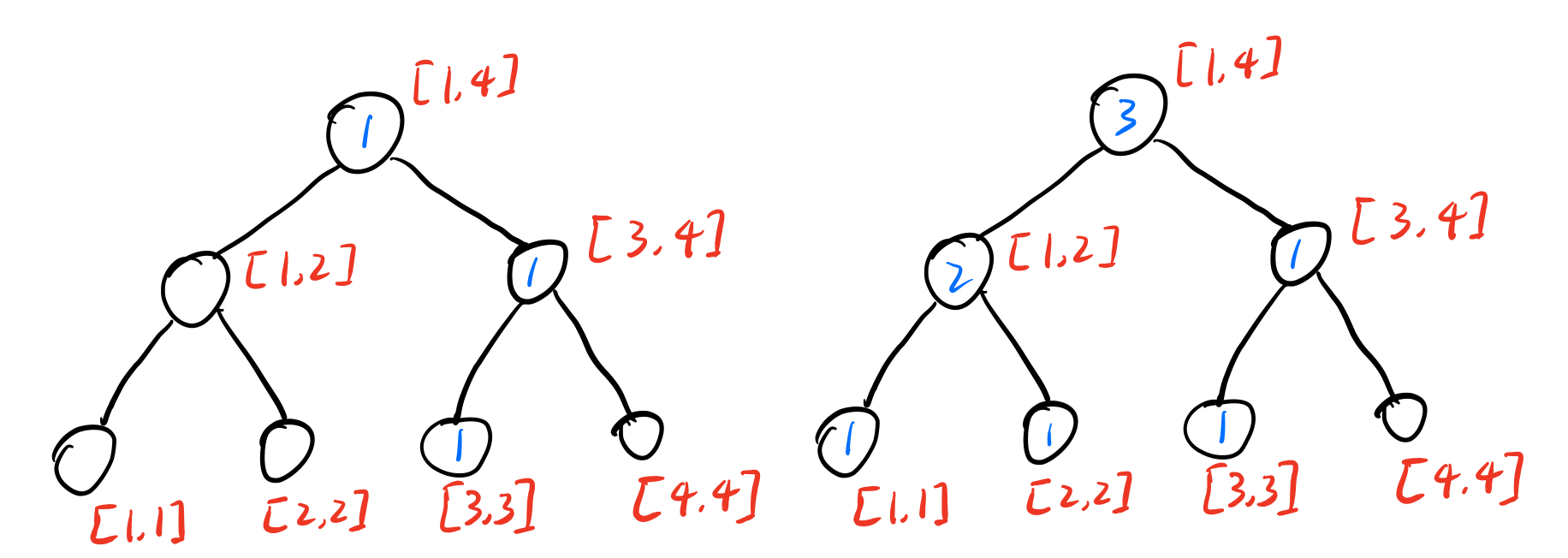
• 我们发现对应节点相减，刚刚好是([2,3])区间内某个范围数的个数，比如说([1,2])这个节点相减为(2)，说明在原序列([2,3])这个区间内有两个数在([1,2])范围内。([3,4])相减为(0)，说明原序列([2,3])区间中没有数字在([3,4])范围内。

• 那我们从根节点开始，计算左孩子范围的数字(num)，如果(kleq num)，说明第(k)小的数字在左子树中，递归进入左子树，否则进入右子树。

• 空间分析：

  • 因为我们是动态开点，首先最初的线段树有(2n-1)个节点，每次操作会增加(logn)个节点。最坏情况下总结点数(2n-1+nlogn)，那么对于(10^5)来讲，开(20*10^5)较为妥当，但这时候还是不要吝惜空间比较好，所以直接用(2^5*10^5)开空间。

• 至此，问题解决，详见代码。

#include<bits/stdc++.h>
using namespace std;

const int maxn = 2e5 + 10;
int a[maxn], num[maxn], n, m, len;

int sum[maxn<<5]; //sum(i)存储根为i的子树的大小
int ls[maxn<<5];  //左儿子
int rs[maxn<<5];  //右儿子
int rt[maxn<<5];  //根节点
int tot;          //一共出现多少个根

int build(int l, int r)
{
    int root = ++tot;
    if(l == r) return root;
    int mid = (l + r) >> 1;
    ls[root] = build(l, mid);
    rs[root] = build(mid+1, r);
    return root;   //返回这课子树的根节点
}

//插入操作
int update(int pre, int l, int r, int k)
{
    int root = ++tot;
    ls[root] = ls[pre], rs[root] = rs[pre], sum[root] = sum[pre] + 1;
    if(l == r) return root;
    int mid = (l + r) >> 1;
    //更改左子树或右子树
    if(k <= mid) ls[root] = update(ls[pre], l, mid, k);
    else rs[root] = update(rs[pre], mid+1, r, k);
    return root;
}

//查询操作
int query(int u, int v, int l, int r, int k)
{
    if(l == r) return l;
    int x = sum[ls[v]] - sum[ls[u]];
    int mid = (l + r) >> 1;
    if(k <= x) return query(ls[u], ls[v], l, mid, k);
    else return query(rs[u], rs[v], mid+1, r, k - x);
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        num[i] = a[i];
    }

    //离散化
    sort(num+1, num+1+n);
    len = unique(num+1, num+1+n) - num - 1;

    rt[0] = build(1, len);
    for(int i = 1; i <= n; i++)
    {
        int t = lower_bound(num+1, num+1+len, a[i]) - num;
        rt[i] = update(rt[i-1], 1, len, t);
    }
    int l, r, k;
    while(m--)
    {
        scanf("%d%d%d", &l, &r, &k);
        int ans = query(rt[l-1], rt[r], 1, len, k);
        printf("%d
", num[ans]);
    }

    return 0;
}