复数基础知识

复数基础知识

0：前言

此为FFT基础知识

我们以前都学过，如果一个数要开平方的话，一定要保证被开平方的数是一个正数，但是为了扩充数域，引入复数概念。

规定(sqrt{-1}=i)。

1：复数的概念

形如(z=x+iy)的数就是一个复数，其中(x)和(y)是任意的实数，分别称为复数(z)的实部和虚部。

一般来说，复数不能比大小，但是可以说两个复数相等。

2：复数的代数运算

加减就对应实部虚部相加就行了。

乘法和除法需要稍加注意。

乘法：

[z_1z_2=(x_1+y_1i)(x_2+y_2i)=x_1x_2+x_1y_2i+x_2y_1i-y_1y_2=(x_1x_2-y_1y_2)+(x_1y_2+x_2y_1)i ]

除法：

[frac{z_1}{z_2}=frac{x_1+y_1i}{x_2+y_2i}=frac{(x_1+y_1i)(x_2-y_2i)}{(x_2+y_2i)(x_2-y_2i)}=frac{(x_1+y_1i)(x_2-y_2i)}{x_2^2+y_2^2} ]

之后对上面做乘法就行，也就是说复数的除法要将分母实化。

同样复数满足交换律、结合律、分配律。

3：复数的几何表示

任意一个复数(z=x+y_i)都有一个与之对应的二维平面点对((x,y))。

如图所示：

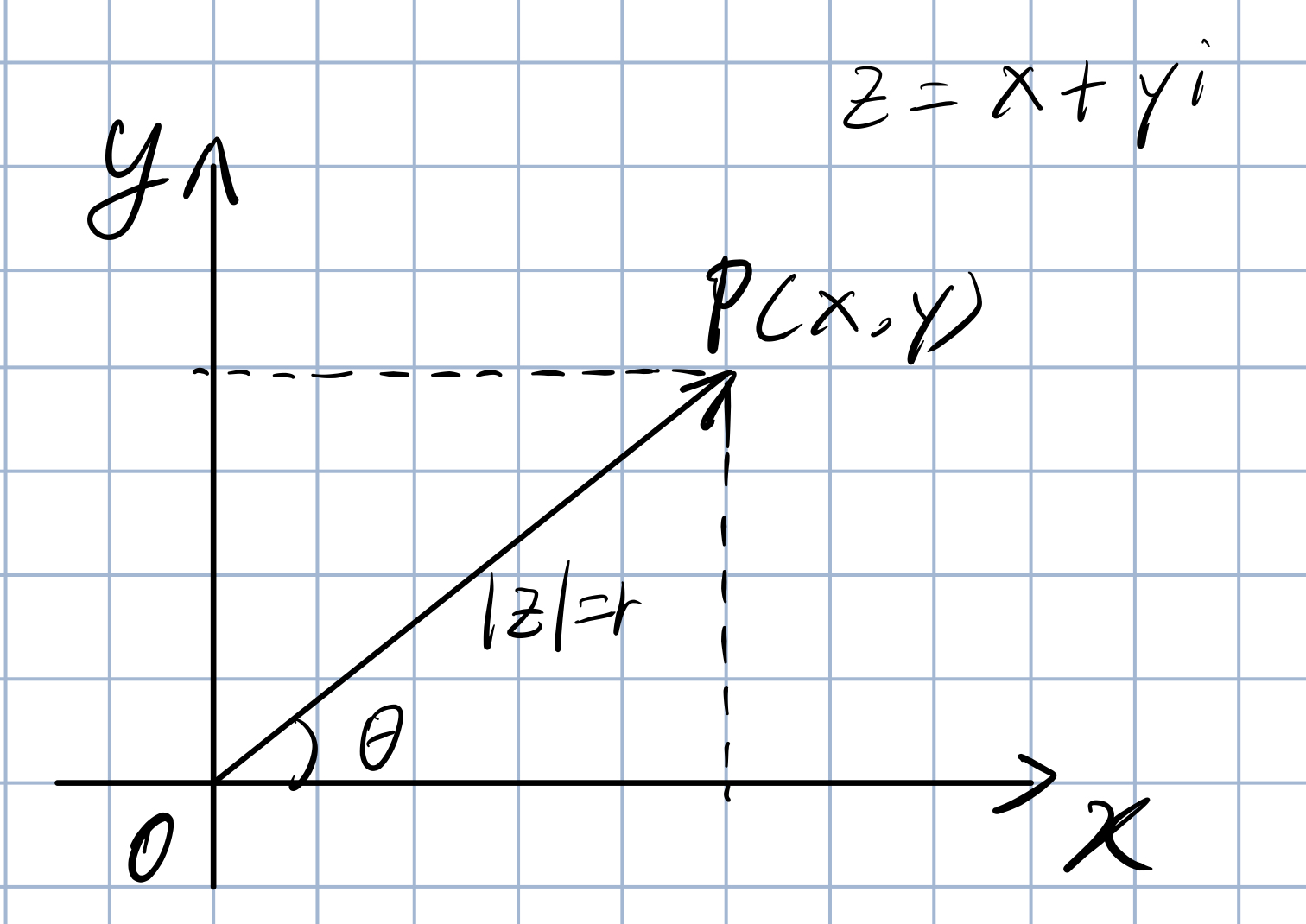
其中

• (|z|=r=sqrt{x^2+y^2})，表示这个向量的模或长度。
• ( heta=arctanfrac{y}{x})表示向量所对应的幅角。
  • 特殊的，当(z=0)时，幅角不确定。
• 也可以知道(x=rcos heta,y=rsin heta)。

接着我们可以得到复数的另一种表示：

[z=x+yi=rcos heta+irsin heta=r(cos heta+isin heta)=re^{i heta} ]

即(z=re^{i heta}).

其中(e^{i heta}=cos heta+isin heta)就是大名鼎鼎的欧拉((Euler))公式。（(e)是自然对数）

值得注意的一点！！

我们说( heta)表示复数(z)的幅角，但其实幅角的表示可以不唯一。

比如说我从( heta)的位置正好逆时针旋转一圈后变成( heta+2pi)，他还是在那个位置，但是他不等于( heta)。

所以说幅角可以表示为( heta+2kpi)，其中(k)取任意整数。

既然有很多个幅角，我们可以定义一个幅角主值，也就是我们最开始的那个( heta)，不去加(2kpi)。

但是比如说(frac{pi}{2})(逆时针扫)，他同样可以用(-frac{3pi}{2})(顺时针扫)来表示。

我们规定在(x)轴上方的用逆时针扫的角度，(x)轴下方用顺时针扫的角度。

仔细理解这点，后面对复数开根号需要用到。

4：复数的幂与方根

1：复数的积与商

设有两个复数(z_1=r_1e^{i heta_1},z_2=r_2e^{i heta_2})。

[z_1z_2=r_1r_2e^{i( heta_1+ heta_2)} ]

[frac{z_1}{z_2}=frac{r_1}{r_2}*e^{i( heta_1- heta_2)} ]

所以可以得到以下两个定理：

• 两个复数乘积的模等于他们模的乘积；两个复数乘积的幅角等于他们幅角的和。
• 两个复数商的模等于他们模的商；两个复数商的幅角等于他们幅角的差。

2：复数的幂与方根

幂

首先引入一个公式：

[(cos heta+isin heta)^n=cosn heta+isinn heta ]

这就是棣莫弗((De Moivre))公式。

(z^n)就是(n)个(z)乘起来，所以有：

[z^n=r^ne^{in heta}=r^n(cosn heta+isinn heta) ]

方根（重点）

要求复数(z)的(n)次方根，实际上就是求解方程(w^n=z)，问(w)。

设

[z=re^{i heta},w= ho e^{ivarphi} ]

从而得到方程

[ ho ^n=r\nvarphi= heta+2kpi ]

解得：

[ ho=sqrt[n]{r}\varphi=frac{ heta+2kpi}{n} ]

所以：

[w_k=sqrt[n]{r}e^{i(frac{2kpi+ heta}{n})} ]

当(k=0,1,2,...,n-1)时，可以得到(n)个相异的根：

[w_0=sqrt[n]{r}e^{ifrac{ heta}{n}},w_1=sqrt[n]{r}e^{ifrac{ heta+2pi}{n}},w_2=sqrt[n]{r}e^{ifrac{ heta+4pi}{n}},...,w_{n-1}=sqrt[n]{r}e^{ifrac{ heta+2(n-1)pi}{n}} ]

为什么只有(n)个呢？因为(k)取别的整数的话，所得到的根就和上述的(n)个根重复了。

由复数的几何意义可知，最后这(n)个根就表示他们以原点为圆心，以(sqrt[n]{r})为半径在一个圆上均匀分布着。

就像这样：

这里表示有四个根，

蓝线的四个头。

来做个例题收尾吧

求(sqrt[4]{1+i})：

[ecause1+i=sqrt{2}e^{ifrac{pi}{4}}\ herefore sqrt[4]{1+i}=sqrt[8]{2}e^{ifrac{frac{pi}{4}+2kpi}{4}},k=0,1,2,3 ]

有：

[w_0=sqrt[8]{2}e^{ifrac{pi}{16}},w_1=sqrt[8]{2}e^{ifrac{9pi}{16}},w_2=sqrt[8]{2}e^{ifrac{17pi}{16}},w_3=sqrt[8]{2}e^{ifrac{25pi}{16}} ]

这四个根表示以原点为圆心，以(sqrt[8]{2})为半径的圆内接正方形的四个顶点。