洛谷5490:【模板】扫描线(线段树求矩形面积并)
题意描述:
- 求(n)个矩形的面积并。
输入格式:
- 第一行输入一个整数(n)。
- 接下来(n)行每行输入四个非负整数(x_1,y_1,x_2,y_2),表示一个矩形的左下角坐标为((x_1,y_1)),右上角坐标为((x_2,y_2))。
输出格式:
- 输出一个正整数表示,表示(n)个矩形的并集覆盖的总面积。
数据范围:
- (1leq nleq 10^5,0leq x_1,x_2,y_1,y_2leq 10^9)。
思路:
-
线段树求矩形面积并
-
-
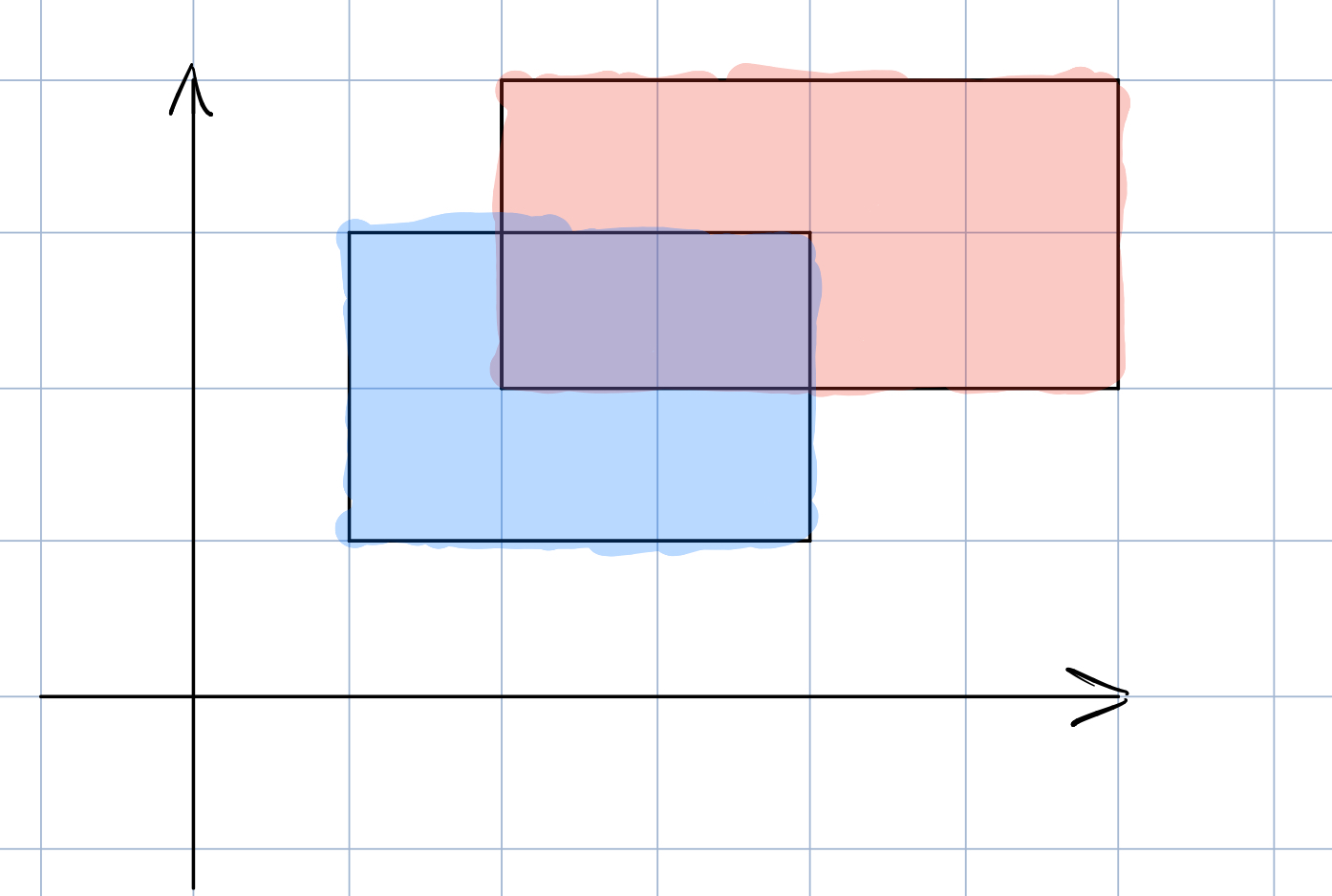
考虑这样一个两个矩形相交,划分一下面积,有:
-
-
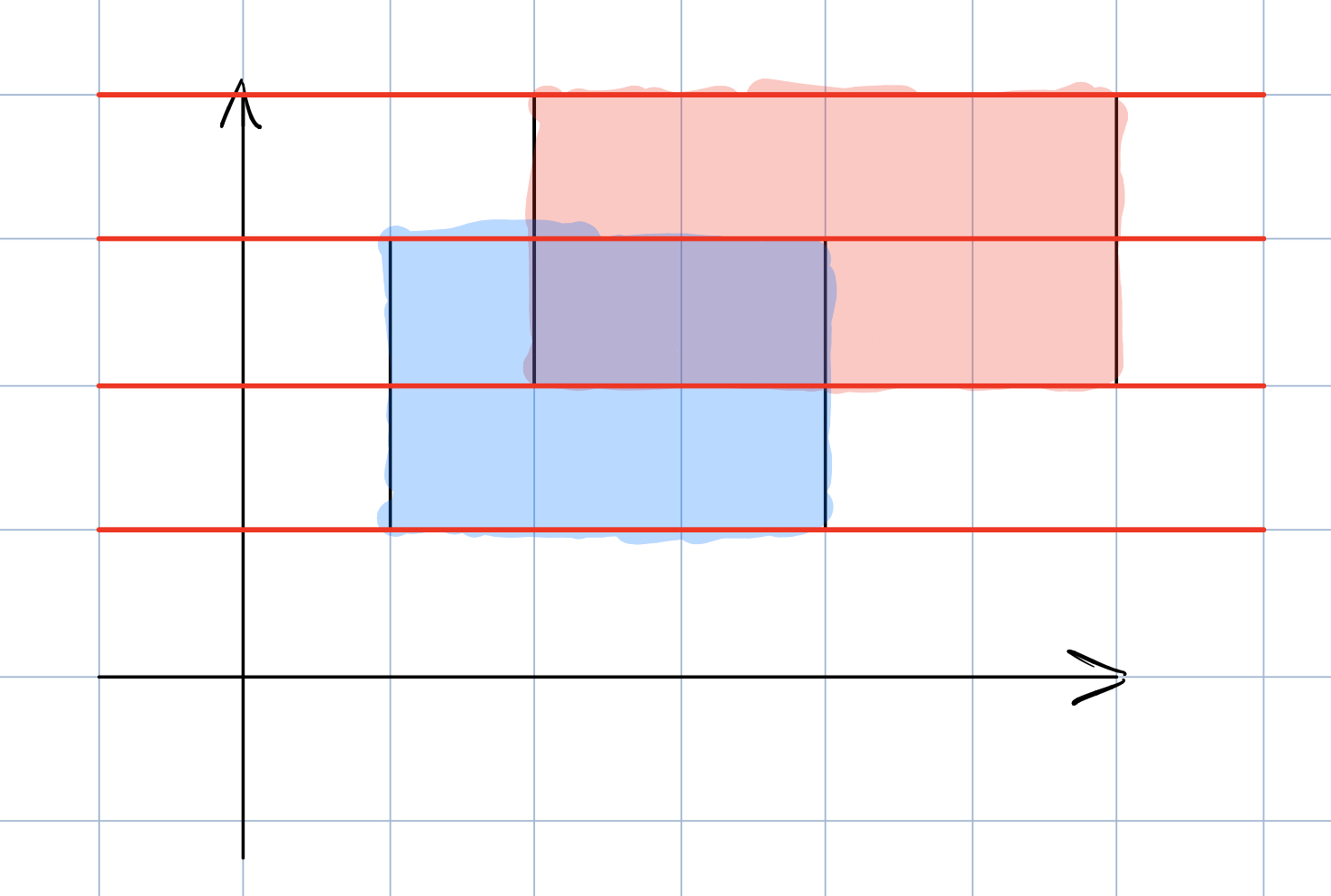
这样原先的图形就被分成了三份,每份图形的形状都规整(矩形)。
-
也就是说,这时候用一条扫描线,从下往上扫,每次碰到一条横边就停下来,计算面积后累加至答案当中。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 10;
typedef long long ll;
int n;
ll x_axis[maxn<<1];
struct ScanLine
{
ll l, r, h;
int mark;
bool operator < (const ScanLine b) const{
return h < b.h;
}
}line[maxn<<1];
struct SegmenTree
{
int l, r;
int sum; //被完全覆盖的次数
ll len; //区间内被截的长度
#define lson p<<1
#define rson p<<1|1
#define l(x) tree[x].l
#define r(x) tree[x].r
#define sum(x) tree[x].sum
#define len(x) tree[x].len
}tree[maxn<<2];
void build(int p, int l, int r)
{
l(p) = l, r(p) = r;
if(l == r) return;
int mid = (l+r)>>1;
build(lson, l, mid);
build(rson, mid+1, r);
}
void pushup(int p)
{
if(sum(p))
len(p) = x_axis[r(p)+1]-x_axis[l(p)];
else
len(p) = len(lson) + len(rson);
}
void change(int p, ll l, ll r, int c)
{
//l r表示需要修改的真实区间
//l(p),r(p)表示线段树该节点管辖的下标范围
if(x_axis[r(p)+1] <= l || r <= x_axis[l(p)])
return; //不在维护的范围内
//完全覆盖
if(l <= x_axis[l(p)] && x_axis[r(p)+1] <= r)
{
sum(p) += c;
pushup(p);
return;
}
change(lson, l, r, c);
change(rson, l, r, c);
pushup(p);
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
ll x1, x2, y1, y2;
scanf("%lld%lld%lld%lld", &x1, &y1, &x2, &y2);
x_axis[2*i-1] = x1, x_axis[2*i] = x2;
line[2*i-1] = {x1, x2, y1, 1}; //左下角
line[2*i] = {x1, x2, y2, -1}; //右上角
}
n <<= 1;
sort(line+1, line+1+n);
sort(x_axis+1, x_axis+1+n);
int tot = unique(x_axis+1, x_axis+1+n) - x_axis - 1;
build(1, 1, tot-1); //tot个点中间有tot-1个区间
ll ans = 0;
for(int i = 1; i < n; i++) //最后一条线不考虑
{
//将扫描线的信息导入线段树
change(1, line[i].l, line[i].r, line[i].mark);
//累加答案
ans += tree[1].len*(line[i+1].h-line[i].h);
}
cout << ans << endl;
return 0;
}