在互联网发展的早期,电子邮件的发送是基于两个主机之间直接连接的TCP。但是这必须是双方都在线的情况下才能行的通。如果接收方不在线,那么发送方会等待一段时间后尝试重发邮件。这种传输机制的可靠性是非常高的,但是其有效性却非常低下。后来出现了电子邮件服务器,发送方和接收方就不必同时在线。发送方发出的电子邮件在邮件服务器中,邮件服务器会根据邮件DNS的MX来查询接收方的邮件服务器IP地址,然后将邮件转发到接收方的邮件服务器。接收方就能从它的服务器上获取邮件。例如:你使用网易邮箱给QQ邮箱发送了一封邮件,那么他就是按照上面的过程到达QQ邮箱的。
电子邮件需要一个邮件地址。现在互联网上使用的邮件地址的格式是这样的:邮箱名称@域名。例如:bbq@163.com。现在的电子邮件地址也是由DNS来管理的(MX记录)。
STMP
STMP是发送电子邮件的协议,默认使用25端口。STMP在传输层使用TCP协议建立一个连接,在这个连接上进行控制,应答以及数据的发送。客户端以文本的形式发送请求,服务器端返回一个状态码来进行应答。下面使用telnet来发送邮件,以了解其详细过程。Windows Vista之后的操作系统默认是不开启telnet的,在win10下,首先需要开启telnet。在win10的设置中搜索“控制面板”。如下所示:

在控制面板中打开“程序选项”。

然后选择启用或关闭Windows功能。
在弹出的窗口中勾选Telnet客户端,然后点击确定,等待服务启用。启用服务以后,重启电脑即可使用telnet。

重启电脑以后,打开命令行(CMD)。然后键入如下命令:

SMTP服务默认端口是25,所以命令如上。
接下来的操作如下:
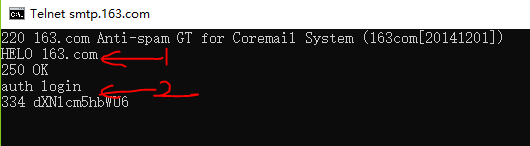
auth login键入之后,就可以登录你的邮箱了,这里需要base64编码格式的用户名以及密码。这就需要你用一个工具去转换相应的编码方式。我没有转换工具,也懒得弄了。在线工具又怕那些网站盗取你邮箱密码。有兴趣的可以自己接着向下搞搞。
随着电子邮件的发展,铺天盖地的广告随之而来。SMTP本身没法验证发送者,不像QQ一样,需要加好友才能发消息。电子邮件不一样,只要有一个邮箱地址,你就能给这个邮箱发邮件。比如网易邮箱,网易自己的广告都是满天飞的。
上面所说的SMTP服务只能传输文本文件,后来MIME的出现使的电子邮件的内容也大大的丰富了。
MIME
MIME规定了应用消息的格式,MIME基本由两部分组成,首部不能是空行,一旦出现空行,之后的内容就会被自动认定为正文。在MIME首部中的“Content-Type”中指出了传输信息的格式。
POP
POP协议是接受电子邮件的协议。如前所述,随着电子邮件的发展,出现了邮件服务器。因此,接受邮件也就需要一定的协议。接受端能从POP服务器上获取电子邮件。POP与SMTP一样,也是通过客户端和服务器之间建立一个TCP连接来完成相应的操作。POP的命令也是以ASCII方式。它的应答更为简单,只有 “+OK”和“-ERR”。
也可以使用telnet来登录POP服务器获取刚才上面所发送的电子邮件。登录POP服务器的命令如下:
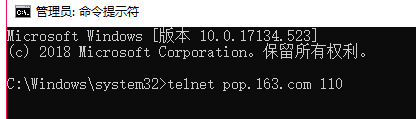
POP服务器默认的端口是110。其余过程不在展示。哦,这个不需要使用base64编码。可以试试。
IMAP
IMAP相比于POP,他是在服务器端管理邮件的,而POP是在客户端管理邮件的。并且正是由于IMAP的出现,人们才可以在各种各样的机器上登录邮箱,使用邮箱。例如,当你在网易邮箱大师上登录你的QQ邮箱的时候,就需要开启IMAP服务。IMAP给我们使用电子邮件带来了巨大的便利。
IMAP由于可以在服务器端管理邮件,因此他能给用户提供更好的体验。例如,已读邮件和未读邮件对于用户来说,无论是在哪一个终端上登录邮箱,他看的信息是同步的。并且还可以单独下载邮件中的某一个附件。例如,一封邮件有5个附件,你可以选择其中的某一个附件进行下载,而不是下载所有附件。这在大文件,低带宽的时候是很有效果的