图（二）——最小生成树、最短路径问题

图（二）——最小生成树、最短路径问题

第十一周课堂学习内容消化——图（二）（三）

本周课堂学习内容

1. 图的遍历
2. 最小生成树
3. 最短路径问题
4. 活动顶点与活动边问题

本周课堂中未理解透彻的地方

1. Prim算法
2. Kruskal算法
3. Dijkstra算法
4. Floyd算法

学习内容总结

贪心算法

研究完Prim算法、Kruskal算法和Dijkstra算法之后，我发现他们都属于贪心算法。因此，在要搞懂这两种算法之前，应该先弄明白贪心算法是什么。

一、简述贪心算法

所谓贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架，算法设计的关键是贪心策略的选择。必须注意的是，贪心算法不是对所有问题都能得到整体最优解，选择的贪心策略必须具备无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。
所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。

二、贪心算法的基本思路

1. 建立数学模型来描述问题。
2. 把求解的问题分成若干个子问题。
3. 对每一子问题求解，得到子问题的局部最优解。
4. 把子问题的解局部最优解合成原来解问题的一个解。

三、贪心算法适用的问题

贪心策略适用的前提是：局部最优策略能导致产生全局最优解。
实际上，贪心算法适用的情况很少。一般，对一个问题分析是否适用于贪心算法，可以先选择该问题下的几个实际数据进行分析，就可做出判断。

动态规划

Floyd算法是一种典型的动态规划。在研究Floyd算法之前，我们先来研究一下这个动态规划。

一、简述动态规划

动态规划过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

动态规划的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

由于动态规划解决的问题多数有重叠子问题这个特点，为减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。

与分治法最大的差别是：适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）。

二、动态规划的基本思路

1. 分析最优解的性质，并刻画其结构特征。
2. 递归的定义最优解。
3. 以自底向上或自顶向下的记忆化方式（备忘录法）计算出最优值
4. 根据计算最优值时得到的信息，构造问题的最优解

三、动态规划适用的问题

能采用动态规划求解的问题的一般要具有3个性质：

1. 最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。
2. 无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。
3. 有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

Prim算法和Kruskal算法

弄明白贪心算法怎么回事之后，接下啦就开始挨个分析这几个算法啦~

一、算法简述

Prim算法和Kruskal算法都是实现最小生成树的算法，都属于贪心算法。

首先，先弄清最小生成树的概念与特点：
最小生成树及各边的权值总和最小的生成树。其中，若最小生成树n个顶点，那么他的边就有n-1个。若每个边的权值都是最小的，那么整体加起来就一定是最小的，这里并不存在后继型，因此在实现最小生成树时可以运用贪心算法。

接下来是Prim算法和Kruskal算法实现最小生成树的方法：
Prim算法：
核心思想：将点分为两拨，已经加入最小生成树的，和未加入的。找到未加入中距离集合最近的点，添加该点，修改其它点到集合的距离,直到所有结点都加入到最小生成树。

Kruskal算法：
核心思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。其中判断是否回路为核心。

二、算法过程演示

以课上中给出的图为例：

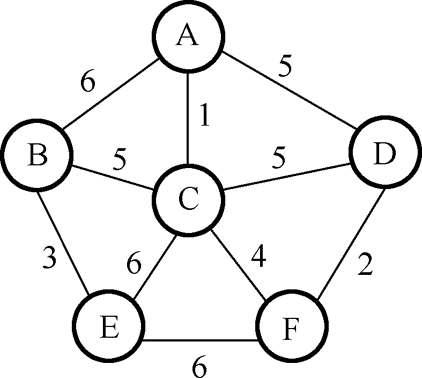
Prim算法：

1. 随机选择一个点作为初始点。这里我选择顶点A。
2. 找到A周围权值最小的边（这里最小的是权值为1的A-C边），加入对应的顶点C。
3. 将A-C看做整体后，再寻找这个整体周围权值最小的边。在这里是C-F边，加入顶点F。
4. 重复以上步骤，由于若最小生成树n个顶点，那么他的边就有n-1个，因此循环n-1次即可

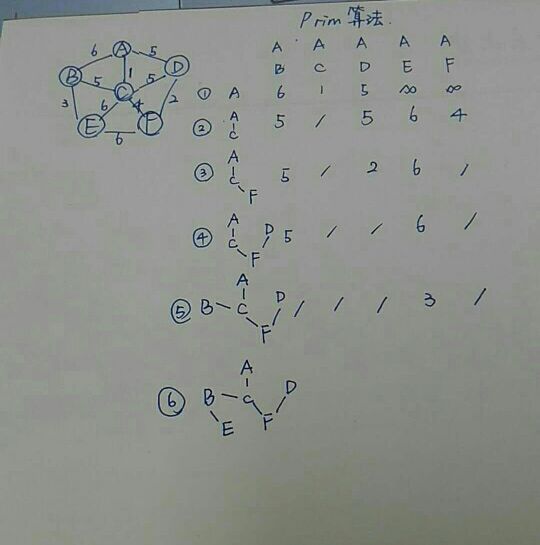
Kruskal算法：

1. 首先将各边按照权值有小到大排序
2. 判断回路：
   • A、B、C、D、E、F的下标分别为0,1,2,3,4,5
   • 他们的初始值均先赋为-1
   • 从最小的权值边开始，两个顶点随便设定一个作为根结点，将根结点的值减一，另一个顶点值改为根结点的下标
   • 在加边的时候，若两个点的值相同，或者其中一个的值为根结点的下标，则会构成回路，应该排除这样的情况。
   • 重复以上的步骤，至少需要循环判断n-1次，一直到找到n-1条符合条件的边才停止。

Dijkstra算法和Floyd算法

一、算法简述

Dijkstra算法和Floyd算法都是广度优先搜索的算法，目的是解决最短路径问题。其中，Dijkstra算法也是一种贪心算法，而Floyd算法更多的是一种动态规划。

Dijkstra算法：
Dijkstra算法为最短路径中的单源最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。注意该算法要求图中不存在负权边。解决的是图中任意一个顶点到其他顶点的最短距离。

设G为赋权有向图或无向图，G边上的权均非负。
求G中从顶点u0到其余点的最短路。
S：具有永久标号的顶点集。
对每个顶点，定义两个标记（l(v) , z(v)），其中，
l(v)：表示从顶点u0到v的一条路的权。
z(v)：v的父亲点，用以确定最短路的路线。
算法的过程就是在每一步改进这两个标记，使最终l(v)为从顶点u0到v的最短路的权。输入为带权邻接矩阵W。

Floyd算法：
Floyd算法是各顶点对间最短路径算法，解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。

D（i , j）：i 到 j 的距离
R（i , j）：i 到 j 之间的插入点
输入带权邻接矩阵W，

1. 赋初值：对所有 i , j ，d ( i , j ) ← w ( i , j ) , r ( i , j ) ← j , k←1。
2. 更新 d ( i , j ) , r ( i , j )：对所有 i , j , 若 d ( i , k ) + d ( k , j ) ＜d ( i , j ) ，则
   d ( i , j ) ← d ( i , j ) + d ( i , j )， r ( i , j ) ← k
3. 若 k = v ，停止；否则 k ← k + 1，转2

参考资料

• 五大常用算法之三：贪心算法
• 五大常用算法之三：动态规划
• Prim最小生成树算法详解
• Kruskal算法 之 Java详解
• 最短路径——Dijkstra算法和Floyd算法