最近在网上也看了不少相关深度学习的视频,大部分都在讲解原理,对代码的实现讲解较少,为此苦苦寻找一本实战的书籍,黄天不负有心人,终于找到一本很好的书籍,<深度学习之TensorFlow入门、原理与进阶实战>,作者是李金洪。在这里就记录一下我的学习之路,也希望对和我一样在学习深度学习路上迷茫的同学有一定的帮助。
一、解决问题
本节内容来源于书中第三章内容,TensorFlow基本开发步骤-以线性回归拟合二维数据为例。
本节主要解决一个什么问题呢?假设我们有一组数据集,数据集是二维的,其中x和y对应的关系近似为y=2x,我们的目的就是从这度数据中求解出y和x之间这样的关系。
我们在解决这样的问题过程中积累了一定的规律。主要遵循以下步骤:
- 准备数据
- 搭建模型
- 迭代训练
- 使用模型进行预测
二、准备数据
数据我们可以利用y=2x的公式来生成带有一定干扰噪声的数据集。
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt ''' 一准备数据 ''' #设定训练集数据长度 n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据 train_x = np.linspace(-1,1,n_train) #把x乘以2,加入(0,0.3)的高斯正太分布 train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=n_train) #绘制x,y波形
plt.figure() plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点
plt.legend()
plt.show()
我们可以看一看生成的数据点

三、搭建模型
因为只有一个因变量,所以逻辑线性回归方程为 y = w1x+b,也可以看做神经网络中一个神经元,只有两个参数w1和b。我们可以搭建一个这样的模型,代码如下:
''' 二 搭建模型 ''' ''' 前向反馈 ''' #创建占位符 input_x = tf.placeholder(dtype=tf.float32) input_y = tf.placeholder(dtype=tf.float32) #模型参数 w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重 b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构 pred = tf.multiply(w,input_x) + b ''' 反向传播bp ''' #定义代价函数 选取二次代价函数 cost = tf.reduce_mean(tf.square(input_y - pred)) #设置求解器 采用梯度下降法 学习了设置为0.001 train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost)
四、迭代模型
我们可以定义代价函数为二次代价函数,然后利用梯度下降法求解参数,代码如下:
''' 三 迭代模型 ''' #设置迭代次数 training_epochs = 200 display_step = 20 with tf.Session() as sess: #初始化所有张量 sess.run(tf.global_variables_initializer()) #存放批次值和代价值 plotdata = {'batch_size':[],'loss':[]} #开始迭代 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): #开始执行图 sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息 if epoch % display_step == 0: #计算代价值 loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}) print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数 if not loss == np.nan: plotdata['batch_size'].append(epoch) plotdata['loss'].append(loss) #输出最终结果 print('Finished!') print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b)))
运行程序输出结果如下:

我们可以看到w的值近似为2,b近似为0,这正是我们之前假设的公式参数。
五、模型预测
我们预测输入为2,4,5,7时输出的值:
#预测 test_x = [2,4,5,7] test_y = sess.run(pred,feed_dict={input_x:test_x}) print('prediction ',test_y)

六、可视化显示
为了能够直观的显示我们生产的模型,可训练的状态值,我们通过plt绘制线性回归模型和迭代的代价值。
''' 四 可视化显示 ''' #绘制原数据点,和估计曲线 plt.figure(figsize=(4.2*2,3.2*1)) plt.subplot(121) plt.plot(train_x,train_y,'ro',label='Original data') plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data') plt.legend() #绘制代价曲线 plt.subplot(122) plt.plot(plotdata['batch_size'],plotdata['loss'],'b--') plt.xlabel('batch_size') plt.ylabel('loss') plt.title('Minibatch run vs. Training loss') plt.show()
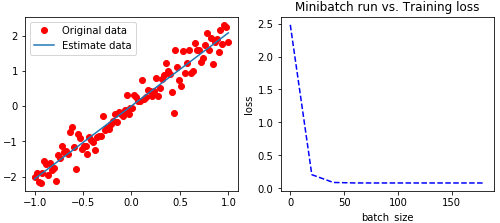
左图中的斜线,是模型中w和b为常量所组成的关于x与y的直线方程。可以看到是一条几乎y=2x的直线。
右图中我们可以看到刚开始损失值一直在下降,后面趋近平稳。
完整代码如下:

# -*- coding: utf-8 -*- """ Created on Tue Apr 17 15:12:35 2018 @author: zy """ import tensorflow as tf import numpy as np import matplotlib.pyplot as plt ''' 一准备数据 ''' #设定训练集数据长度 n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据 train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布 train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形 plt.figure() plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点 plt.legend() plt.show() ''' 二 搭建模型 ''' ''' 前向反馈 ''' #创建占位符 input_x = tf.placeholder(dtype=tf.float32) input_y = tf.placeholder(dtype=tf.float32) #模型参数 w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重 b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构 pred = tf.multiply(w,input_x) + b ''' 反向传播bp ''' #定义代价函数 选取二次代价函数 cost = tf.reduce_mean(tf.square(input_y - pred)) #设置求解器 采用梯度下降法 学习了设置为0.001 train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) ''' 三 迭代模型 ''' #设置迭代次数 training_epochs = 200 display_step = 20 with tf.Session() as sess: #初始化所有张量 sess.run(tf.global_variables_initializer()) #存放批次值和代价值 plotdata = {'batch_size':[],'loss':[]} #开始迭代 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): #开始执行图 sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息 if epoch % display_step == 0: #计算代价值 loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}) print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数 if not loss == np.nan: plotdata['batch_size'].append(epoch) plotdata['loss'].append(loss) #输出最终结果 print('Finished!') print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测 test_x = [2,4,5,7] test_y = sess.run(pred,feed_dict={input_x:test_x}) print('prediction ',test_y) ''' 四 可视化显示 ''' #绘制原数据点,和估计曲线 plt.figure(figsize=(4.2*2,3.2*1)) plt.subplot(121) plt.plot(train_x,train_y,'ro',label='Original data') plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data') plt.legend() #绘制代价曲线 plt.subplot(122) plt.plot(plotdata['batch_size'],plotdata['loss'],'b--') plt.xlabel('batch_size') plt.ylabel('loss') plt.title('Minibatch run vs. Training loss') plt.show()
