在我们使用TensorFlow的时候,有时候需要训练一个比较复杂的网络,比如后面的AlexNet,ResNet,GoogleNet等等,由于训练这些网络花费的时间比较长,因此我们需要保存模型的参数。
编程基础案例中主要讲解模型的保存和恢复,以及使用几个案例使我们更好的理解这一块内容。
一 保存和载入模型
1.保存模型
首先需要建立一个saver,然后在session中通过saver的save即可将模型保存起来,代码如下:
''' 1.保存模型 ''' ''' 这里是各种构建模型graph的操作,省略.... ''' #创建saver对象 saver = tf.train.Saver() with tf.Session() as sess: #初始化张量 sess.run(tf.global_variables_initializer()) ''' 这里是将数据喂入模型进行训练,省略... ''' #训练完成后,保存模型,如果file_name不存在,会自动创建 saver.save(sess,'save_path/file_name')
2.载入模型
载入模型只需要调用saver对象的restore()函数,会从指定的路径找到模型文件,并覆盖到相关参数中,代码如下:
''' 2.载入模型 ''' #创建saver对象 saver = tf.train.Saver() with tf.Session() as sess: #参数可以进行初始化,也可以不进行初始化,即使进行了初始化,初始化的值也会被restore的值覆盖掉 sess.run(tf.global_variables_initializer()) saver.restore(sess,'save_path/file_name')
二 保存/载入线性回归模型
在第四节我们讲了线性回归的案列,这里我们就保存这个案例的模型,然后恢复
''' 3.保存和恢复线性回归模型 ''' import numpy as np import matplotlib.pyplot as plt import os ''' 一准备数据 ''' #设定训练集数据长度 n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据 train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布 train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形 plt.figure() plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点 plt.legend() plt.show() #重置图 (不清空该图的所有缓存) tf.reset_default_graph() ''' 二 搭建模型 ''' ''' 前向反馈 ''' #创建占位符 input_x = tf.placeholder(dtype=tf.float32) input_y = tf.placeholder(dtype=tf.float32) #模型参数 w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重 b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构 pred = tf.multiply(w,input_x) + b ''' 反向传播bp ''' #定义代价函数 选取二次代价函数 cost = tf.reduce_mean(tf.square(input_y - pred)) #设置求解器 采用梯度下降法 学习了设置为0.001 train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) ''' 三 迭代模型 ''' #设置迭代次数 training_epochs = 200 display_step = 20 #创建saver对象 在张量声明之后创建 saver = tf.train.Saver() #生成模型的路径 savedir = './LinearRegression' #模型文件 savefile = 'linearmodel.cpkt' #路径不存在创建目录 if not os.path.isdir(savedir): os.mkdir(savedir) with tf.Session() as sess: #初始化所有张量 sess.run(tf.global_variables_initializer()) #恢复模型 if os.path.isfile(os.path.join(savedir, savefile)+'.meta'): saver.restore(sess,os.path.join(savedir,savefile)) #存放批次值和代价值 plotdata = {'batch_size':[],'loss':[]} #开始迭代 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): #开始执行图 sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息 if epoch % display_step == 0: #计算代价值 loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}) print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数 if not loss == np.nan: plotdata['batch_size'].append(epoch) plotdata['loss'].append(loss) #输出最终结果 print('Finished!') print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测 test_x = [2,4,5,7] test_y = sess.run(pred,feed_dict={input_x:test_x}) print('prediction ',test_y) ''' 四 可视化显示 ''' #绘制原数据点,和估计曲线 plt.figure(figsize=(4.2*2,3.2*1)) plt.subplot(121) plt.plot(train_x,train_y,'ro',label='Original data') plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data') plt.legend() #绘制代价曲线 plt.subplot(122) plt.plot(plotdata['batch_size'],plotdata['loss'],'b--') plt.xlabel('batch_size') plt.ylabel('loss') plt.title('Minibatch run vs. Training loss') plt.show() #保存参数 saver.save(sess,os.path.join(savedir, savefile))
我们可以看到在LinearRegression文件夹下面生成了四个文件:

这四个文件主要是:
- .meta(存储网络结构)、包含了这个TF图完整信息:如所有变量等。
- .data和.index(存储训练好的参数,也叫检查点文件)、这是一个二进制文件,包含所有权重,偏置,梯度和所有其他存储的变量的值。
- checkpoint(记录最新的模型)。保存最后的检查点的文件 ,如果同时保存了几个模型,则在这个文件还有这几个模型的变量数据,由于在这几个模型中可能存在同名变量,所以取得的数据可能有问题。所以解决方案是最后把不同模型保存在不同文件夹下,或者使用 tf.variable_scope指定变量名字分组。
我们运行多次这个代码,我们会发现我们每次都是在之前训练的基础上继续训练模型,这是因为每次训练我们都先恢复模型再继续训练。


三 分析模型内容
如何将我们保存的模型内容打印出来呢?这一节将教你如何将生成的模型的内容打印出来,并观察其存放的具体数据方式,同时显示如何将指定内容保存到模型文件中。
1.查看模型内容
''' 3.查看模型内容 ''' from tensorflow.python.tools.inspect_checkpoint import print_tensors_in_checkpoint_file print_tensors_in_checkpoint_file(os.path.join(savedir,savefile),None,True)

tensor_name后面是创建的张量名称,接着是它的数值。
2.保存模型的其它方法
前面我们在创建saver对象的时候没有传入任何参数,实际上,tf.train.Saver()函数还可以传入参数来实现更高级的功能,可以指定存储张量名字与张量的对应关系,可以写成这样:
#或者指定保存参数 代表将张量w,b的值分别放到变量w和b名字中 saver = tf.train.Saver({'w':w,'b':b})
我们也可以这么写:
saver = tf.train.Saver([w,b]) #存放到一个list里面 savee = tf.train.Saver({v.opname:v for v in [w,b]}) #将op的name当做名字
下面展示一个例子:我们可以看到张量a的值被保存到张量名为b_param上,张量b的值保存到张量名为a_param上。
#给a和b分别指定一个固定的值,将它们颠倒文职存放 a = tf.Variable(1.0,name='a') b = tf.Variable(2.0,name='b') #指定保存参数 saver = tf.train.Saver({'b_param':a,'a_param':b}) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) #保存参数 saver.save(sess,'./test.cpkt') print_tensors_in_checkpoint_file('./test.cpkt',None,True)

注意:当我们在Saver()中指定了保存和恢复的变量时,在恢复的时候我们要保证模型文件中有该变量,不然会报错。保存的时候模型文件也只会保存指定的变量。如果我们想保存时除了恢复时指定的变量,还保存其他的所有变量,最好的解决方法是创建两个Saver()对象,一个用于恢复模型,一个用于保存模型。
四 检查点
由于我们在训练过程中可能会出现错误,如果我们在训练一个很大的网络的时候,训练到快结束的时候,突然报错,这样会导致我们之前的训练功亏一篑,我们心里可能就会很崩溃,因此最好的方法就是能够在训练的过程中也保存模型。TensorFlow就提供了一个这样的功能。
在训练中保存模型,我们习惯上称之为保存检查点(checkpoint)。
1.为模型添加保存检查点
为我们之前线性回归的案例追加'保存检查点'功能,通过该功能,可以生成检查点文件,并能够制定生成检查点文件的个数。
这个例子与保存模型的功能类似,只是保存的位置发生了变化,我们希望在显示信息是将检查点保存下来,因此需要在打印信息后面添加检查点。
另外在这里我们会用到Saver()类的另一个参数,max_to_keep = 1,表名最多保存一个检查点文件,这样在迭代过程中,新生成的模型就会覆盖以前的模型。
在保存时使用了如下代码传入了迭代次数:
#每隔display_step轮后保存一次检查点 saver.save(sess,os.path.join(savedir,savefile),global_step = epoch)
TensorFlow会将迭代次数一起放在检查点的文件上,所以在载入时,同样也要指定迭代次数。
# -*- coding: utf-8 -*- """ Created on Wed Apr 18 09:20:53 2018 @author: zy """ ''' 4.检查点(模型训练中保存模型) ''' ''' (1)为模型添加保存检查点(即训练中保存检查点) ''' import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import os ''' 一准备数据 ''' #设定训练集数据长度 n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据 train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布 train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形 plt.figure() plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点 plt.legend() plt.show() tf.reset_default_graph() ''' 二 搭建模型 ''' ''' 前向反馈 ''' #创建占位符 input_x = tf.placeholder(dtype=tf.float32) input_y = tf.placeholder(dtype=tf.float32) #模型参数 w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重 b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构 pred = tf.multiply(w,input_x) + b ''' 反向传播bp ''' #定义代价函数 选取二次代价函数 cost = tf.reduce_mean(tf.square(input_y - pred)) #设置求解器 采用梯度下降法 学习了设置为0.001 train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) ''' 三 迭代模型 ''' #设置迭代次数 training_epochs = 200 display_step = 20 #生成Saver对象 saver = tf.train.Saver(max_to_keep = 1) #生成模型的路径 savedir = './LinearRegression' #模型文件 savefile = 'linearmodel.cpkt' #路径不存在创建目录 if not os.path.isdir(savedir): os.mkdir(savedir) with tf.Session() as sess: #初始化所有张量 sess.run(tf.global_variables_initializer()) #恢复模型 if os.path.isfile(os.path.join(savedir, savefile)+'.meta'): saver.restore(sess,os.path.join(savedir,savefile)) #存放批次值和代价值 plotdata = {'batch_size':[],'loss':[]} #开始迭代 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): #开始执行图 sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息 if epoch % display_step == 0: #计算代价值 loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}) print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数 if not loss == np.nan: plotdata['batch_size'].append(epoch) plotdata['loss'].append(loss) #每隔display_step轮后保存一次检查点 saver.save(sess,os.path.join(savedir,savefile),global_step = epoch) #输出最终结果 print('Finished!') print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测 test_x = [2,4,5,7] test_y = sess.run(pred,feed_dict={input_x:test_x}) print('prediction ',test_y) ''' 四 可视化显示 ''' #绘制原数据点,和估计曲线 plt.figure(figsize=(4.2*2,3.2*1)) plt.subplot(121) plt.plot(train_x,train_y,'ro',label='Original data') plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data') plt.legend() #绘制代价曲线 plt.subplot(122) plt.plot(plotdata['batch_size'],plotdata['loss'],'b--') plt.xlabel('batch_size') plt.ylabel('loss') plt.title('Minibatch run vs. Training loss') plt.show() #重启一个session,载入检查点 方法一 load_epoch = 180 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) saver.restore(sess,os.path.join(savedir,savefile+'-'+str(load_epoch))) test_x = [2,4,5,7] test_y = sess.run(pred,feed_dict={input_x:test_x}) print('prediction ',test_y)
运行完后,我们会看到多了几个文件,多的那几个文件就是检查点文件:这里有必要说一下180怎么来的,180就是我们最后一次保存检查点的迭代次数
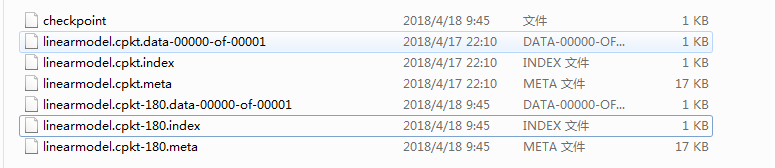
在载入模型时,我们每次都要指定迭代次数,因此会比较麻烦,这里有几种种方法,直接载入最近保存的检查点文件,个人推荐第三种代码如下:、
''' 由于恢复模型,需要指定迭代次数,比较麻烦,我们可以直接载入最近保存的检查点文件 方法二 ''' with tf.Session() as sess: #需要指定检查点文件所在目录 ckpt = tf.train.get_checkpoint_state(savedir) if ckpt and ckpt.model_checkpoint_path: saver.restore(sess,ckpt.model_checkpoint_path) ''' 或者 方法三 ''' with tf.Session() as sess: ckpt = tf.train.latest_checkpoint(savedir) if ckpt != None: #恢复模型 saver.restore(sess,ckpt) #使用默认图,即我们定义的线性回归模型 并获取模型中的tensor graph = tf.get_default_graph() weight = graph.get_tensor_by_name('w:0') bias = graph.get_tensor_by_name('b:0') print(sess.run([w,b])) #在加载的模型后继续加载新的网络层 add_on_op = tf.multiply(w,2) print(sess.run(add_on_op)) ''' 或者 直接把网络结构加载进来(.meta),不可以重写网络结构,不然会出现变量重命名冲突问题。 方法四 ''' #清空默认图的内容 tf.reset_default_graph() with tf.Session() as sess: #加载以前保存的网络 将保存在.meta文件中的图添加到当前的图中 new_saver = tf.train.import_meta_graph(os.path.join(savedir,savefile)+'.meta') #从指定目录下获取最近一次检查点 new_saver.restore(sess,tf.train.latest_checkpoint(savedir)) #使用加载的模型 并获取模型中的tensor graph = tf.get_default_graph() weight = graph.get_tensor_by_name('w:0') bias = graph.get_tensor_by_name('b:0') print(sess.run([weight,bias])) #在加载的模型后继续加载新的网络层 add_on_op = tf.multiply(weight,2) print(sess.run(add_on_op))
运行结果如下:

这里有几点需要注意:上面介绍了四种类恢复模型的方法,前三种类似,可以概括为一类,最后一种比较特殊:
- 第一种是saver.restore(sess, 'aaaa.ckpt')类型的,这种方法的本质是读取全部参数,并加载到已经定义好的网络结构上,因此相当于给网络的weights和biases赋值并执行tf.global_variables_initializer()。这种方法的缺点是使用前必须重写网络结构,而且网络结构要和保存的参数完全对上。
- 第二种就比较高端,直接把网络结构加载进来(.meta),不可以重写网络结构,不然会出现变量重命名冲突问题。
2.更简便地保存检查点
这里介绍使用tf.train.MonitoredTrainingSession函数来保存检查点,该函数可以直接实现保存和载入检查点模型的文件。与上一个案例不同的是,这里并不是按照循环步数来保存,而是按照训练时间来保存,通过指定save_checkpoint_secs参数的具体秒数,来设置每训练多久保存一次检查点。
''' (2) 使用tf.train.MonitoredTrainingSession按时间来保存检查点 ''' #清空默认图的内容 tf.reset_default_graph() #设置检查点路径 savedir = './LinearRegression/checkpoints' global_step = tf.train.get_or_create_global_step() #通过向 "ref" 添加 "value" 来更新 "ref"。此操作在更新完成后输出 "ref"。 step = tf.assign_add(global_step,1) with tf.train.MonitoredTrainingSession(checkpoint_dir = savedir,save_checkpoint_secs = 2) as sess: print(sess.run([global_step])) #启用死循环,当sess不结束时就不停止 while not sess.should_stop(): #运行自加1操作 i =sess.run(step) print(i)
巡行结果如下:
并且在检查点路径下生成如下文件:
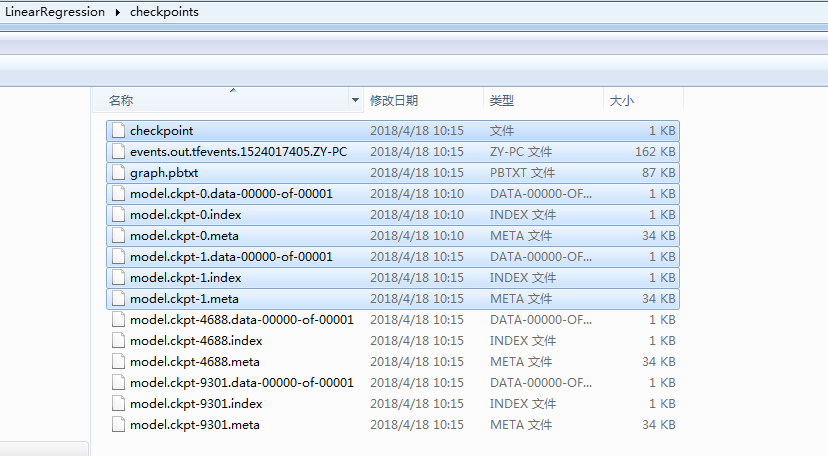
在使用该方法有两点需要注意:
- save_checkpoint_secs参数默认时间是10分钟。
- 使用该方法,必须定义global_step变量,否则会报错。
注意:程序中如果有定义检查点文件的保存路径savedir,则该路径必须是相对路径,且以./开头,比如./data,不然运行时加载模型可能会出错。
完整代码:

# -*- coding: utf-8 -*- """ Created on Tue Apr 17 20:56:00 2018 @author: zy """ import tensorflow as tf ''' TensorFlow 编程基础上 这一节主要讲解模型的保存和恢复,以及使用几个案例使我们更好的理解这一块内容。 ''' ''' 1.保存模型 ''' ''' 这里是各种构建模型graph的操作,省略.... ''' #创建saver对象 saver = tf.train.Saver() with tf.Session() as sess: #初始化张量 sess.run(tf.global_variables_initializer()) ''' 这里是将数据喂如模型进行训练,省略... ''' #训练完成后,保存模型,如果file_name不存在,会自动创建 saver.save(sess,'save_path/file_name') ''' 2.载入模型 ''' #创建saver对象 saver = tf.train.Saver() with tf.Session() as sess: #参数可以进行初始化,也可以不进行初始化,即使进行了初始化,初始化的值也会被restore的值覆盖掉 sess.run(tf.global_variables_initializer()) saver.restore(sess,'save_path/file_name') ''' 3.保存和恢复线性回归模型 ''' import numpy as np import matplotlib.pyplot as plt import os ''' 一准备数据 ''' #设定训练集数据长度 n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据 train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布 train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形 plt.figure() plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点 plt.legend() plt.show() #重置图 tf.reset_default_graph() ''' 二 搭建模型 ''' ''' 前向反馈 ''' #创建占位符 input_x = tf.placeholder(dtype=tf.float32) input_y = tf.placeholder(dtype=tf.float32) #模型参数 w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重 b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构 pred = tf.multiply(w,input_x) + b ''' 反向传播bp ''' #定义代价函数 选取二次代价函数 cost = tf.reduce_mean(tf.square(input_y - pred)) #设置求解器 采用梯度下降法 学习了设置为0.001 train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) ''' 三 迭代模型 ''' #设置迭代次数 training_epochs = 200 display_step = 20 #创建saver对象 在张量声明之后创建 #saver = tf.train.Saver() #或者指定保存参数 代表将张量w,b的值分别放到变量w和b名字中 saver = tf.train.Saver({'w':w,'b':b}) #或者写成 #saver = tf.train.Saver([w,b]) #存放到一个list里面 #savee = tf.train.Saver({v.opname:v for v in [w,b]}) #将op的name当做名字 #生成模型的路径 savedir = './LinearRegression' #模型文件 savefile = 'linearmodel.cpkt' #路径不存在创建目录 if not os.path.isdir(savedir): os.mkdir(savedir) with tf.Session() as sess: #初始化所有张量 sess.run(tf.global_variables_initializer()) #恢复模型 if os.path.isfile(os.path.join(savedir, savefile)+'.meta'): saver.restore(sess,os.path.join(savedir,savefile)) #存放批次值和代价值 plotdata = {'batch_size':[],'loss':[]} #开始迭代 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): #开始执行图 sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息 if epoch % display_step == 0: #计算代价值 loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}) print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数 if not loss == np.nan: plotdata['batch_size'].append(epoch) plotdata['loss'].append(loss) #输出最终结果 print('Finished!') print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测 test_x = [2,4,5,7] test_y = sess.run(pred,feed_dict={input_x:test_x}) print('prediction ',test_y) ''' 四 可视化显示 ''' #绘制原数据点,和估计曲线 plt.figure(figsize=(4.2*2,3.2*1)) plt.subplot(121) plt.plot(train_x,train_y,'ro',label='Original data') plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data') plt.legend() #绘制代价曲线 plt.subplot(122) plt.plot(plotdata['batch_size'],plotdata['loss'],'b--') plt.xlabel('batch_size') plt.ylabel('loss') plt.title('Minibatch run vs. Training loss') plt.show() #保存参数 saver.save(sess,os.path.join(savedir, savefile)) ''' 3.查看模型内容 ''' from tensorflow.python.tools.inspect_checkpoint import print_tensors_in_checkpoint_file print_tensors_in_checkpoint_file(os.path.join(savedir,savefile),None,True) #给a和b分别指定一个固定的值,将它们颠倒文职存放 a = tf.Variable(1.0,name='a') b = tf.Variable(2.0,name='b') #指定保存参数 saver = tf.train.Saver({'b_param':a,'a_param':b}) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) #保存参数 saver.save(sess,'./test.cpkt') print_tensors_in_checkpoint_file('./test.cpkt',None,True)

# -*- coding: utf-8 -*- """ Created on Wed Apr 18 09:20:53 2018 @author: zy """ ''' 4.检查点的适用(模型训练中保存模型) ''' ''' (1)为模型添加保存检查点(即训练中保存检查点) ''' import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import os ''' 一准备数据 ''' #设定训练集数据长度 n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据 train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布 train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形 plt.figure() plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点 plt.legend() plt.show() tf.reset_default_graph() ''' 二 搭建模型 ''' ''' 前向反馈 ''' #创建占位符 input_x = tf.placeholder(dtype=tf.float32) input_y = tf.placeholder(dtype=tf.float32) #模型参数 w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重 b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构 pred = tf.multiply(w,input_x) + b ''' 反向传播bp ''' #定义代价函数 选取二次代价函数 cost = tf.reduce_mean(tf.square(input_y - pred)) #设置求解器 采用梯度下降法 学习了设置为0.001 train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) ''' 三 迭代模型 ''' #设置迭代次数 training_epochs = 200 display_step = 20 #生成Saver对象 saver = tf.train.Saver(max_to_keep = 1) #生成模型的路径 savedir = './LinearRegression' #模型文件 savefile = 'linearmodel.cpkt' #路径不存在创建目录 if not os.path.isdir(savedir): os.mkdir(savedir) with tf.Session() as sess: #初始化所有张量 sess.run(tf.global_variables_initializer()) #恢复模型 if os.path.isfile(os.path.join(savedir, savefile)+'.meta'): saver.restore(sess,os.path.join(savedir,savefile)) #存放批次值和代价值 plotdata = {'batch_size':[],'loss':[]} #开始迭代 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): #开始执行图 sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息 if epoch % display_step == 0: #计算代价值 loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}) print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数 if not loss == np.nan: plotdata['batch_size'].append(epoch) plotdata['loss'].append(loss) #每隔display_step轮后保存一次检查点 saver.save(sess,os.path.join(savedir,savefile),global_step = epoch) #输出最终结果 print('Finished!') print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测 test_x = [2,4,5,7] test_y = sess.run(pred,feed_dict={input_x:test_x}) print('prediction ',test_y) ''' 四 可视化显示 ''' #绘制原数据点,和估计曲线 plt.figure(figsize=(4.2*2,3.2*1)) plt.subplot(121) plt.plot(train_x,train_y,'ro',label='Original data') plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data') plt.legend() #绘制代价曲线 plt.subplot(122) plt.plot(plotdata['batch_size'],plotdata['loss'],'b--') plt.xlabel('batch_size') plt.ylabel('loss') plt.title('Minibatch run vs. Training loss') plt.show() ''' 重启一个session,载入检查点 方法一 ''' load_epoch = 180 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) saver.restore(sess,os.path.join(savedir,savefile+'-'+str(load_epoch))) test_x = [2,4,5,7] test_y = sess.run(pred,feed_dict={input_x:test_x}) print('prediction ',test_y) ''' 由于恢复模型,需要指定迭代次数,比较麻烦,我们可以直接载入最近保存的检查点文件 方法二 ''' with tf.Session() as sess: #需要指定检查点文件所在目录 ckpt = tf.train.get_checkpoint_state(savedir) if ckpt and ckpt.model_checkpoint_path: saver.restore(sess,ckpt.model_checkpoint_path) ''' 或者 方法三 ''' with tf.Session() as sess: ckpt = tf.train.latest_checkpoint(savedir) if ckpt != None: #恢复模型 saver.restore(sess,ckpt) #使用默认图,即我们定义的线性回归模型 并获取模型中的tensor graph = tf.get_default_graph() weight = graph.get_tensor_by_name('w:0') bias = graph.get_tensor_by_name('b:0') print(sess.run([w,b])) #在加载的模型后继续加载新的网络层 add_on_op = tf.multiply(w,2) print(sess.run(add_on_op)) ''' 或者 直接把网络结构加载进来(.meta),不可以重写网络结构,不然会出现变量重命名冲突问题。 方法四 ''' #清空默认图的内容 tf.reset_default_graph() with tf.Session() as sess: #加载以前保存的网络 将保存在.meta文件中的图添加到当前的图中 new_saver = tf.train.import_meta_graph(os.path.join(savedir,savefile)+'.meta') #从指定目录下获取最近一次检查点 new_saver.restore(sess,tf.train.latest_checkpoint(savedir)) #使用加载的模型 并获取模型中的tensor graph = tf.get_default_graph() weight = graph.get_tensor_by_name('w:0') bias = graph.get_tensor_by_name('b:0') print(sess.run([weight,bias])) #在加载的模型后继续加载新的网络层 add_on_op = tf.multiply(weight,2) print(sess.run(add_on_op)) ''' (2) 使用tf.train.MonitoredTrainingSession按时间来保存检查点 ''' #清空默认图的内容 tf.reset_default_graph() #设置检查点路径 savedir = './LinearRegression/checkpoints' global_step = tf.train.get_or_create_global_step() #通过向 "ref" 添加 "value" 来更新 "ref"。此操作在更新完成后输出 "ref"。 step = tf.assign_add(global_step,1) with tf.train.MonitoredTrainingSession(checkpoint_dir = savedir,save_checkpoint_secs = 2) as sess: print(sess.run([global_step])) #启用死循环,当sess不结束时就不停止 while not sess.should_stop(): #运行自加1操作 i =sess.run(step) print(i)
