逻辑回归

转自公众号《数据科学家联盟》，作者饼干

一、逻辑回归：

逻辑回归假设数据服从伯努利分布，通过极大似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

逻辑回归是一个非线性模型，但是是其背后是以线性回归为理论支撑的。

提出一个与线性模型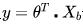 长相类似但不同的新公式：假设特征X所对应的y值是在指数上变化，那么就可以将结果y值取对数，作为其线性模型逼近的目标。也就是所谓的“对数线性回归”：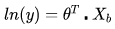

在“对数线性回归”的公式中，可以改写为 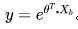 。实际上是在求输入空间X到输出空间y的非线性函数映射。对数函数的作用是将线性回归模型的预测值与真实标记联系起来。

因此可以得到一个一般意义上的单调可微的“联系函数”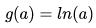：。其本质就是给原来线性变换加上一个非线性变换(或者说映射)，使得模拟的函数有非线性的属性，但本质上调参还是线性的，主体是内部线性的调参。

那么对于解决分类问题的逻辑回归来说，我们需要找到一个“联系函数”，将线性回归模型的预测值与真实标记联系起来。

将“概率”转换为“分类”的工具是“阶梯函数”：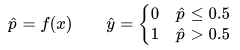

但是这个阶梯函数不连续，不能作为“联系函数”g，因此使用对数几率函数来在一定程度上近似阶梯函数，将线性回归模型的预测值转化为分类所对应的概率。

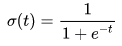
 如果另y为正例，1-y为负例，所谓的“几率”就是二者的比值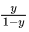 。几率反映了样本x为正例的相对可能性。

“对数几率”就是对几率取对数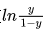 ，对数几率实际上就是之前提到的sigmoid函数，将线性模型转化为分类。

如果令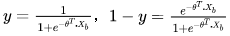 。带入到对数几率中 。

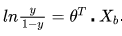可以看出，sigmoid实际上就是用线性回归模型的预测结果取逼近真实值的对数几率，因此逻辑回归也被称为“对数几率回归”。

1、损失函数：

1.0.1：

已经知道逻辑回归的模型：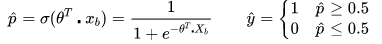

 那么，如何求出未知参数θ呢？

首先回顾一下线性回归。在线性回归中，做法如下：

由于已知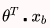 是估计值，于是用估计值与真值的差来度量模型的好坏。使用MSE（差值的平方和再平均）作为损失函数。然后就可以通过导数求极值的方法，找到令损失函数最小的θ了。

那么在逻辑回归中，解决思路也大致类似。

逻辑回归和线性回归最大的区别就是：逻辑回归解决的是分类问题，得到的y要么是1，要么是0。而我们估计出来的p是概率，通过概率决定估计出来的p到底是1还是0。因此，也可以将损失函数分成两类：

• 如果给定样本的真实类别y=1，则估计出来的概率p越小，损失函数越大（估计错误）
• 如果给定样本的真实类别y=0，则估计出来的概率p越大，损失函数越大（估计错误）

那么将用什么样的函数表示这两种情况呢，可以使用如下函数：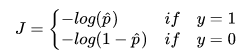

 

分析上面的公式：

• 当y=1时，损失函数为 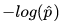。特点是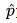：越趋于0，损失（loss）越大；越趋于1，损失（loss）越小。

• 分析如下：      
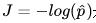
  是一个单调递减函数，且概率p的值域只能是[0,1]之间，因此只有函数的上半部分。我们看到当概率p取0（即预估的分类结果y=0）时，loss值是趋近于正无穷的，表明我们分错了（实际分类结果是1）。

• 当y=0时，损失函数为 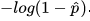。特点是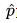： 越趋于1，损失（loss）越大；越趋于0，损失（loss）越小。

• 分析如下：   
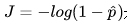
  是一个单调递减函数，且概率p的值域只能是[0,1]之间，因此只有函数的上半部分。我们看到当概率p取1（即预估的分类结果y=1）时，loss值是趋近于正无穷的，表明我们分错了（实际分类结果是0）。

由于模型是个二分类问题，分类结果y非0即1，因此我们可以使用一个巧妙的方法，通过控制系数的方式，将上面的两个式子合并成一个：

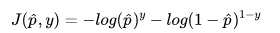
 以上是对于单个样本的误差值，那么求整个集合内的损失可以取平均值：

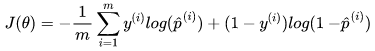
 然后，我们将  替换成sigmoid函数，得到逻辑回归的损失函数如下：

 

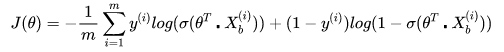
 1.0.2：

我们已经知道了逻辑损失函数的推导过程，但是就像在数学课上老师在黑板中写下的解题过程一样，我们费解的是“这个思路究竟是怎么来的”？

逻辑回归的损失函数当然不是凭空出现的，而是根据逻辑回归本身式子中系数的最大似然估计推导而来的。

最大似然估计就是通过已知结果去反推最大概率导致该结果的参数。极大似然估计是概率论在统计学中的应用，它提供了一种给定观察数据来评估模型参数的方法，即 “模型已定，参数未知”，通过若干次试验，观察其结果，利用实验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

逻辑回归是一种监督式学习，是有训练标签的，就是有已知结果的，从这个已知结果入手，去推导能获得最大概率的结果参数，只要我们得出了这个参数，那我们的模型就自然可以很准确的预测未知的数据了。

令逻辑回归的模型为 ，则可以将其视为类1的后验概率，所以有：

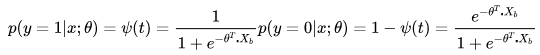
以上两个式子，可以改写为一般形式：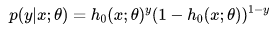

 因此根据最大似然估计，可以得到：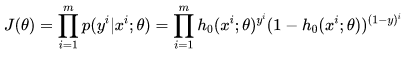

 为了简化计算，取对数将得到：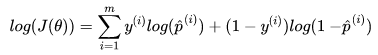

 我们希望极大似然越大越好，就是说，对于给定样本数量m，希望越小越好，得到逻辑回归的损失函数如下：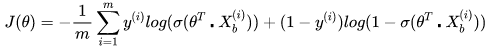

所以说逻辑回归的损失函数不是定义出来的，而是根据最大似然估计推导出来的。

下面的目标就是：找到一组参数theta，使得损失函数J(theta)达到最小值。

这个损失函数是没有标准方程解的，因此在实际的优化中，我们往往直接使用梯度下降法来不断逼近最优解。

2、梯度：

对于损失函数：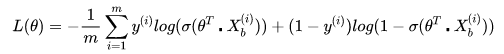

 使用梯度下降法，就要求出梯度，对每一个向量中每一个参数，都求出对应的导数：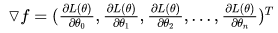

 对sigmoid函数进行求导（链式求导法则）：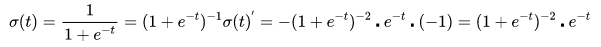

 然后对外层的log函数进行求导：

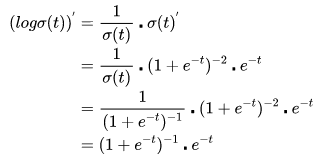
然后进行整理：

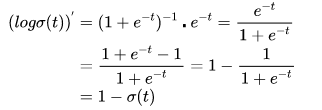
下面就可以对损失函数前半部分的表达式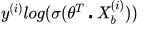：对θ进行求导了。带入上面的结果，得到：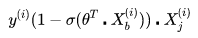

 同样地，可以对损失函数的后半部分做求导，跟上面类似。

最终求的损失函数L(θ)对θ的导数如下，即逻辑回归的损失函数经过梯度下降法对一个参数进行求导，得到结果如下：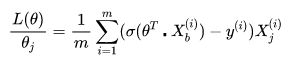

 其中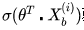 就是逻辑回归模型的预测值。

在求得对一个参数的导数之后，则可以对所有特征维度上对损失函数进行求导，得到向量化后的结果如下：

3、决策边界：

二、代码实现及sklearn逻辑回归