个人理解:
虽然很多介绍PCA的文章,但大多基于PCA的矩阵原理,没有与实际应用相结合的解释。而且,我也一直困惑在R中应用PCA的输入和输出的设置。所以我写了下文。
主要参考此文档:http://strata.uga.edu/software/pdf/pcaTutorial.pdf,并结合自己的数据整理了下面内容。此文档浅显易懂,特别好。
1. 坐标旋转:rotating the data
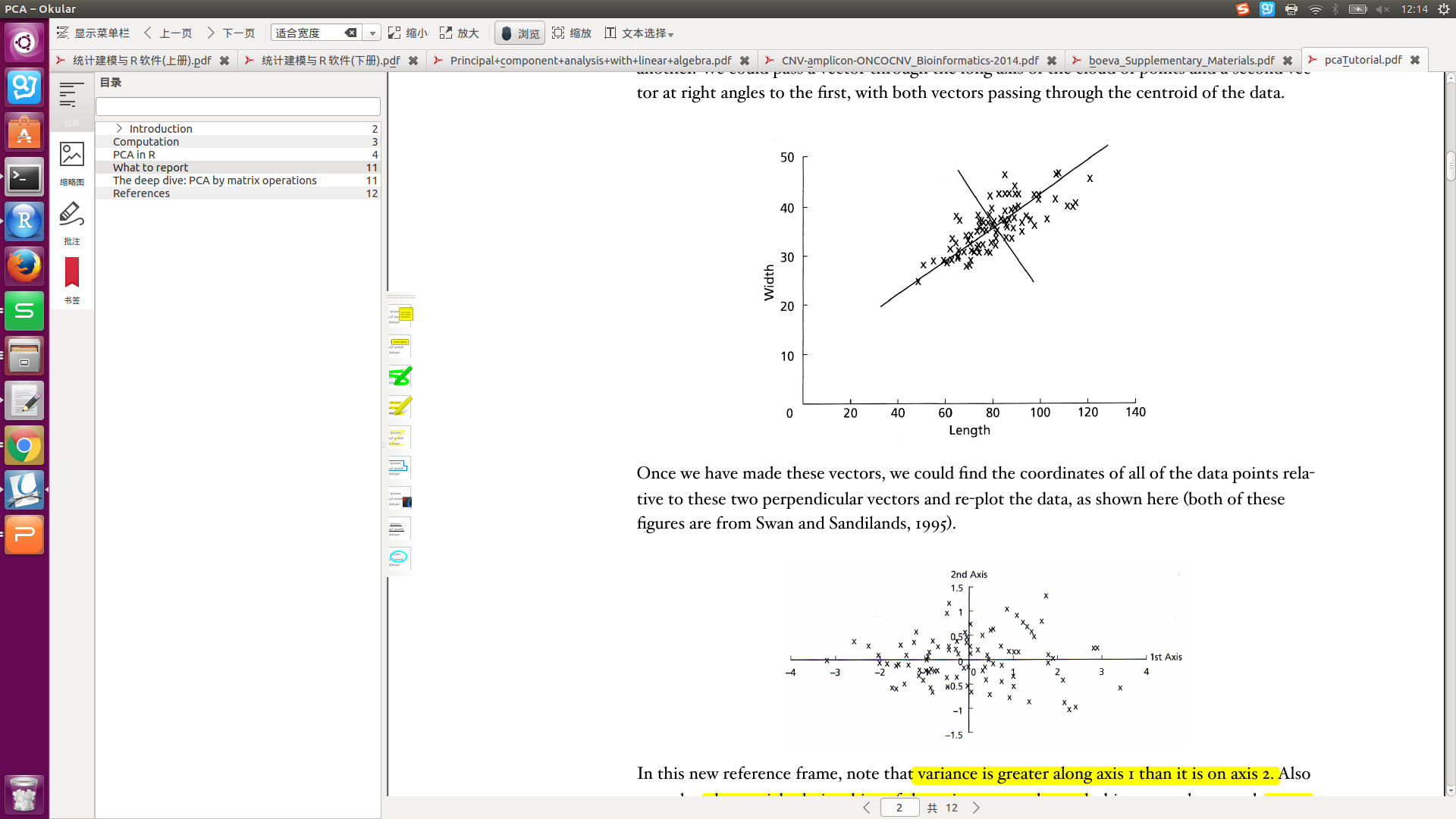
转换后的坐标轴,称为:new vector, or axes。主成分(PC)的坐标轴一般不与原始变量的坐标轴重合。
PCA(Principal Components Analysis):通过坐标旋转来降维的方法。
PC:对original variable的线性组合产生的坐标轴axes,称为PC。
对我的启发:将多维与坐标轴的概念联系起来,维度可以看做是坐标轴。比如,gene expression中的gene可看做维度、坐标轴,gene expression是上面概念中的original variable。
2. PC的计算、与original variable的关系。
数据:p个variable ×n个sample的矩阵。下式中,X1,X2,..., Xp,表示original variable,即gene个数、描述花朵特征的个数。
PC计算过程:
PC1: Y1=a11X1 + a12X2 +...+ a1pXp, 或:用矩阵的形式表示:Y1=a1X
PC2: Y2=a21X1 + a22X2 +...+ a2pXp
....
PC的讲解:
最多有p个主成分,与original variable的数目一致。
比如:参考数据1有4个变量,有4个主成分;参考数据3中有32个变量,主成分最多就是32个。即:有多少个变量,最多就有多少个主成分(PC1,PC2,...);有多少个样本,每个主成分PC1(PC2...)就有多少个值。
对主成分个数的理解:当Cumulative Proportion值为1时,主成分就终止了。因为此时,用PC1,PC2,...就能够涵盖所有的样本了。
对每个主成分的值(比如,参考数据1的PC1有150个值),应该怎么理解呢?PCA图为什么展示这些值呢?
特征向量:
从original variable —> PC之间的变换,可以表示为:Y = XA。 A:特征向量矩阵Sx。每一列是一个特征向量。A中的元素aij,称为权重。该矩阵即为loadings,或下面R输出结果中的rotation。
3.scores。即:prcomp执行后的x。
每个observation在PC的坐标系统中的位置,称为scores。它由original variable和权重aij的线性组合计算得出。
比如:第r个sample在第k个PC上的score,计算如下:
Yrk = a1k*xr1 + a2k*xr2 + ... + apk*xrp
比如:样本1在m个基因下有m个值,根据这m个值,可计算得出样本1分别在在PC1,PC2,...下面的值(scores)。经常看到的PC1和PC2的散点图就是用这个数据画的。比如:df_pca$x
PC1 PC2 PC3 PC4
1 -2.684125626 -0.319397247 0.027914828 0.0022624371
2 -2.714141687 0.177001225 0.210464272 0.0990265503
......
我的问题:对于两个样本的150个差异表达基因,能做PCA分析吗?基于此问题,做了下面的调查分析。
![]()
1. R中应用PCA:
df_pca <- prcomp(test_dt[,2:3], scale. = T)
数据:
test_dt
gene sample_1 sample_2 1 2-Mar 89.76800 165.58500 2 A2M 5.65995 1.61144
...
转置test_dt:
[,1] [,2] [,3] [,4] [,5] ...
sample1 5.65995 4.47988 3.13712 27.02620 2.074420 ...
sample2 1.61144 1.45420 1.11561 6.32818 0.643795 ...
结果:
df_pca
Standard deviations:
[1] 1.187434e+01 1.380454e-14
Rotation:
PC1 PC2
[1,] -0.08421519 0.990887087
[2,] -0.08421519 -0.014023869
[3,] -0.08421519 -0.002650131
...
[141,] -0.08421519 -0.008337000
df_pca$x:
PC1 PC2 sample1 -8.396428 7.677019e-15 sample2 8.396428 -7.534771e-15
2. 结果分析:
summary(df_pca):
Importance of components:
PC1 PC2
Standard deviation 11.87 1.38e-14
Proportion of Variance 1.00 0.00e+00
Cumulative Proportion 1.00 1.00e+00
由此可以看到:
141个变量,2个样本的数据,得到了两个主成分:PC1和PC2。PC1的Cumulative Proportion是1,说明用一个主成分PC1就可以区分这两个样本。
rotation的值中,PC1的权重值都一样-0.08421519,说明由:PC1=aX1+aX2+...+aX141。此处的X1,...是一个矩阵,是两个样本在141个变量上的值的矩阵。
pca$x得到4个值,如果画PC1和PC2的图,则图中只有两个点。且,这两个是对角线的关系。(这样的图不可以)
PC1的方差值很大。
结论:两个样本的141个变量,无法进行主成分分析。
从PCA的原理来看,它是想要进行降维,将多个变量描述的事情,降维为几个新变量就可以描述。一般样本数大于变量数。
PCA的缺点:
1. 对维度进行的是线性变化,对于不能应用线性变化的数据不适用;
2. 对于降维后的坐标系,不容易解释。
问题(内容与上面有重复):
问题1:PCA输入的行和列数据的设置问题。
解决:参考https://www.biostars.org/p/13011/
如果想查看在样本之间哪些gene的差异最大,那么,行是sample,列是gene。You want to see which genes that mean the most for the differences between the samples, and therefore your samples should be in the rows and your genes should be in the columns.
所以,对于上面的数据,我应该转置变为下面的数据,然后再利用prcomp函数,即:prcomp(t(test_dt)):
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] ... sample1 89.768 5.65995 34.7021 26.3499 2.31851 27.3431 8.88269 42.4083 27.3434 32.7261 21.1033 12.3434 ... sample2 165.585 1.61144 60.9142 42.8840 1.07268 45.9556 16.95460 70.6224 45.4109 78.1433 45.4268 20.5639 ...
同时,参考PCA的原理,它处理的是:m个(样本)n维(gene表达值)数据。一般,n行×m列。即:每一列表示一个向量。
从这个角度来看,每一列表示的是一个向量(一个样本的数据),每一行表示的是描述这个样本(或这个向量)的信息。
参考:https://blog.csdn.net/daaikuaichuan/article/details/53444639
如此一来,这两种看法是矛盾的。该如何解决?
我认为在R中用prcomp函数进行PCA分析时,行是sample名,列是特征值。参考R中的数据例子,解释如下:
数据1——数据iris,行:不同类型的花或同一种花的不同朵,列:花属性的数据(如:花瓣、花萼的特征)。
> iris[1:3,1:5]
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
...
数据——参考2的数据decathlon2,行:远动员,列:运动员的特征
## X100m Long.jump Shot.put High.jump X400m X110m.hurdle## SEBRLE 11.0 7.58 14.8 2.07 49.8 14.7
## CLAY 10.8 7.40 14.3 1.86 49.4 14.1
## BERNARD 11.0 7.23 14.2 1.92 48.9 15.0
## YURKOV 11.3 7.09 15.2 2.10 50.4 15.3
## ZSIVOCZKY 11.1 7.30 13.5 2.01 48.6 14.2
## McMULLEN 10.8 7.31 13.8 2.13 49.9 14.4
...
数据——数据3:1000行,32列的数据
[,1] [,2] [,3] [,4] [,5] [,6] ......[,32] [1,] -1.01500872 -1.5419889 -1.5330842 -1.2930589 -0.51541855 -0.7001724
[2,] -0.07963674 -0.2751422 -0.8037817 -0.9519072 -1.57334512 -0.7366414
...
以上前两个数据,调用prcomp函数时,如下:prcomp(iris),prcomp(decathlon2)
参考:
https://www.jianshu.com/p/f15625700b3b
http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/112-pca-principal-component-analysis-essentials/#pca-data-format
问题2:PCA输出结果的解释。
> df_pca(参考数据1的输出)
Standard deviations: //主成分的标准方差。与summary(df_pca)中的Standard deviation一致。
[1] 3.807887e-01 3.925231e-17
Rotation: //变量负荷矩阵。列是特征向量。我理解:每个变量(行)对特征向量的贡献度。 用princomp函数时,用loadings表示。在prcomp中,用rotation表示。
// 即:由四个变量怎么得出PC1~PC4的。即original variable的权重的矩阵。 每一列是一个特征向量。
//PC1 = 0.36138659×Sepal.Length + -0.08452251×Sepal.Width + 0.85667061×Petal.Length
PC1 PC2 PC3 PC4 Sepal.Length 0.36138659 -0.65658877 0.58202985 0.3154872 Sepal.Width -0.08452251 -0.73016143 -0.59791083 -0.3197231 Petal.Length 0.85667061 0.17337266 -0.07623608 -0.4798390 Petal.Width 0.35828920 0.07548102 -0.54583143 0.7536574
> summary(df_pca)(参考数据1的输出) Importance of components: //这一部分的解释参照下面的例子。因为此例子的主成分太少,不好解释。 PC1 PC2 Standard deviation 0.3808 3.925e-17 Proportion of Variance 1.0000 0.000e+00 Cumulative Proportion 1.0000 1.000e+00 //这说明用PC1就能区分所有的样本。
> summary(pZ) (参考数据3的输出) Importance of components: PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10 PC11 PC12 PC13 PC14 Standard deviation 3.6415 2.7178 1.8447 1.3943 1.10207 0.90922 0.76951 0.67490 0.60833 0.51638 0.49048 0.44452 0.40326 0.3904 Proportion of Variance 0.4352 0.2424 0.1117 0.0638 0.03986 0.02713 0.01943 0.01495 0.01214 0.00875 0.00789 0.00648 0.00534 0.0050 Cumulative Proportion 0.4352 0.6775 0.7892 0.8530 0.89288 0.92001 0.93944 0.95439 0.96653 0.97528 0.98318 0.98966 0.99500 1.0000
// Proportion of Variance:每个主成分在区分样本方面,做的贡献度。此行的累积值,就是下一行数据的值。
// Cumulative Proportion:表示用这14个主成分区分样本时,可以完全区分每一个样本。如果用3个主成分,可以区分78.9%的样本。它是上一行数据的累加值。
问题3:如何画图,图的含义?画图函数:
plot(df_pca$x[,1], df_pca$x[,2])
参考:https://mp.weixin.qq.com/s/1f-0DdRH7WU2hAbGRqrECg
图的含义:
n个样本的观察值在新坐标系(PC1,PC2,...)下的位置。比如,样本1在m个基因下有m个值,根据这m个值,可计算得出样本1在PC1,PC2,...下面的值(scores)。比如:
df_pca$x
PC1 PC2 PC3 PC4
1 -2.684125626 -0.319397247 0.027914828 0.0022624371
2 -2.714141687 0.177001225 0.210464272 0.0990265503
3 -2.888990569 0.144949426 -0.017900256 0.0199683897
4 -2.745342856 0.318298979 -0.031559374 -0.0755758166
5 -2.728716537 -0.326754513 -0.090079241 -0.0612585926
6 -2.280859633 -0.741330449 -0.168677658 -0.0242008576
7 -2.820537751 0.089461385 -0.257892158 -0.0481431065
8 -2.626144973 -0.163384960 0.021879318 -0.0452978706
......
150 1.390188862 0.282660938 -0.362909648 -0.1550386282 原始数据有150个样本,4个变量。PCA之后,得到4个主成分。每个样本在这四个主成分下的值为该表。(散点图就是用这些数据画的图)
问题4:如何用ggplot画PCA的图呢?
step1:将prcomp的输出值转成data.frame。
df_pcs<-data.frame(df_pca$x,Species=iris$Species) 或者不用后面Species...也可以。(参考https://www.jianshu.com/p/f15625700b3b)

step2:用ggplot操作df_pcs即可。
参考资料:
PCA是进行降维用的。比如:
检测m个样本的n个基因的表达值,用m个基因的表达值描述这n个样本。即m是属性。
但是,我用n维度的数据(也叫变量。比如基因表达值)去描述、区分这m个样本,太复杂了。我想用3个特征来区分这m个样本。比如:给出3个特征,有90%的样本在这3个特征上都不同。这3个特征就是PC1,PC2和PC3(也叫:主要特征、关键特征、主要变量)。
一般情况下,并不能直接找出这样的主要特征。这时,我们可以用原有维度数据的线性组合(即PC1,PC2,PC3)来表示事物(m个样本)的主要特征, PCA 就是这样一种分析方法。
参考:https://www.biomart.cn/experiment/430/590/597/58034.htm在基因表达数据分析中,使用PCA。
总结:这个总结,真是太好了:
PCA是一种著名的数据降维算法,它应用的条件是数据/特征之间具有明显的线性相关性,它的两个主要的指导思想是抓主要矛盾和方差即信息,它的基本应用是数据降维,以此为基础还有数据可视化、数据压缩存储、异常检测、特征匹配与距离计算等。从数学上理解,它是一种矩阵分解算法;从物理意义上理解,它是线性空间上的线性变换。
————————————————
版权声明:本文为CSDN博主「Chen_Tianyang」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/ctyqy2015301200079/java/article/details/85325125
PCA样本数的问题。解决:https://www.biostars.org/p/217101/
PCA能否用于差异基因分析中?解决:https://support.bioconductor.org/p/56483/
PCA算法原理:https://blog.csdn.net/daaikuaichuan/article/details/53444639
individual&variable的图:http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/118-principal-component-analysis-in-r-prcomp-vs-princomp/#access-to-the-pca-results