http://lightoj.com/volume_showproblem.php?problem=1234
In mathematics, the nth harmonic number is the sum of the reciprocals of the first n natural numbers:
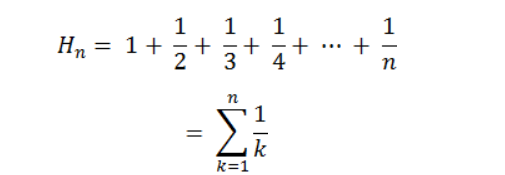
In this problem, you are given n, you have to find Hn.
Input
Input starts with an integer T (≤ 10000), denoting the number of test cases.
Each case starts with a line containing an integer n (1 ≤ n ≤ 108).
Output
For each case, print the case number and the nth harmonic number. Errors less than 10-8 will be ignored.
Sample Input
12
1
2
3
4
5
6
7
8
9
90000000
99999999
100000000
Output for Sample Input
Case 1: 1
Case 2: 1.5
Case 3: 1.8333333333
Case 4: 2.0833333333
Case 5: 2.2833333333
Case 6: 2.450
Case 7: 2.5928571429
Case 8: 2.7178571429
Case 9: 2.8289682540
Case 10: 18.8925358988
Case 11: 18.9978964039
Case 12: 18.9978964139
题意分析:
求
解题思路:
有一个公式 = ln(n+1)+e, e是欧拉常数,但是这公式并不精确。
所以打表会好一点,
直接打表会暴内存,所以每100个打一个表,不够100的再直接计算。
#include <stdio.h>
#define N 1000002
double ans[N];
int main()
{
int T, t=0, n;
for(int i=1; i<N*100-10; i++)
{
ans[i/100+1]+=1.0/i;
if(i%100==0)
{
ans[i/100+1]+=ans[i/100];
ans[i/100]+=1.0/i;
}
}
scanf("%d", &T);
while(T--)
{
scanf("%d", &n);
double sum=0;
for(int i=n/100*100+1; i<=n; i++)
sum+=1.0/i;
printf("Case %d: %.10lf
", ++t, sum+ans[n/100]);
}
return 0;
}