问题描述:已知敌方 100 个目标的经度、纬度如表 1 所示。
经度 纬度
53.7121 15.3046
51.1758 0.0322
46.3253 28.2753
30.3313 6.9348
56.5432 21.4188
10.8198 16.2529
22.7891 23.1045
10.1584 12.4819
20.1050 15.4562
1.9451 0.2057
26.4951 22.1221
31.4847 8.9640
26.2418 18.1760
44.0356 13.5401
28.9836 25.9879
38.4722 20.1731
28.2694 29.0011
32.1910 5.8699
36.4863 29.7284
0.9718 28.1477
8.9586 24.6635
16.5618 23.6143
10.5597 15.1178
50.2111 10.2944
8.1519 9.5325
22.1075 18.5569
0.1215 18.8726
48.2077 16.8889
31.9499 17.6309
0.7732 0.4656
47.4134 23.7783
41.8671 3.5667
43.5474 3.9061
53.3524 26.7256
30.8165 13.4595
27.7133 5.0706
23.9222 7.6306
51.9612 22.8511
12.7938 15.7307
4.9568 8.3669
21.5051 24.0909
15.2548 27.2111
6.2070 5.1442
49.2430 16.7044
17.1168 20.0354
34.1688 22.7571
9.4402 3.9200
11.5812 14.5677
52.1181 0.4088
9.5559 11.4219
24.4509 6.5634
26.7213 28.5667
37.5848 16.8474
35.6619 9.9333
24.4654 3.1644
0.7775 6.9576
14.4703 13.6368
19.8660 15.1224
3.1616 4.2428
18.5245 14.3598
58.6849 27.1485
39.5168 16.9371
56.5089 13.7090
52.5211 15.7957
38.4300 8.4648
51.8181 23.0159
8.9983 23.6440
50.1156 23.7816
13.7909 1.9510
34.0574 23.3960
23.0624 8.4319
19.9857 5.7902
40.8801 14.2978
58.8289 14.5229
18.6635 6.7436
52.8423 27.2880
39.9494 29.5114
47.5099 24.0664
10.1121 27.2662
28.7812 27.6659
8.0831 27.6705
9.1556 14.1304
53.7989 0.2199
33.6490 0.3980
1.3496 16.8359
49.9816 6.0828
19.3635 17.6622
36.9545 23.0265
15.7320 19.5697
11.5118 17.3884
44.0398 16.2635
39.7139 28.4203
6.9909 23.1804
38.3392 19.9950
24.6543 19.6057
36.9980 24.3992
4.1591 3.1853
40.1400 20.3030
23.9876 9.4030
41.1084 27.7149
我方有一个基地,经度和纬度为(70,40)。假设我方飞机的速度为 1000 公里/小时。 我方派一架飞机从基地出发,侦察完敌方所有目标,再返回原来的基地。在敌方每一目 标点的侦察时间不计,求该架飞机所花费的时间(假设我方飞机巡航时间可以充分长)。
旅行商问题,依次给基地编号为1, 最后再编号为102,距离矩阵D = (dij)102*102,将问题转化为求从点1出发,走遍中间所有点,到达点102的一个最短路径。
准备工作:将所给地理坐标在球坐标系中转化为实际距离。
以地心为坐标原点,以赤道平面为XOY平面,以0度经线圈所在的平面为X)Z平面建立球坐标系,设A、B经纬度分别为(x1, y2)、(x2, y2),则其球坐标分别为A(Rcosx1cosy1, Rsinx1cosy1, Rsiny1), B(Rcosx2cosy2, Rsinx2cosy2, Rsiny2),其中R = 6370为地球半径。
则两点之间的实际距离为d = R arccosθ,θ为两个向量的夹角。化简为d = R arccos[cos(x1 - x2)cosy1cosy2 + siny1siny2];
1 load sj.txt 2 x = sj(:, 1);x = x(:); 3 y = sj(:, 2);y = y(:); 4 sj = [x, y]; %d1 = [70, 40];sj = [d1; sj; d1]; 5 sj = sj * pi / 180;%sj是102个位置的经纬度 6 d = zeros(102);%距离矩阵初始化为0 7 %d[i, j] = l = R * arccos[cos(x1 - x2)cosy1cosy2 + siny1siny2] 8 for i = 1 : 101%i->1-101, j->2-102 9 for j = i + 1 : 102 10 temp = cos(sj(i, 1)- sj(j, 1)) * cos(sj(i, 2)) * cos(sj(j, 2)) + sin(sj(i, 2)) * sin(sj(j, 2)); 11 d(i, j) = 6370 * acos(temp); 12 end 13 end 14 d = d + d';% 15 S0 = [1:102]; Sum = 0; 16 for i = 1:101 17 Sum = Sum + d(S0(i),S0(i+1)); 18 end 19 20 S0 = []; Sum = inf; 21 rand('state', sum(clock)); 22 for j = 1 : 1000 23 S = [1 1+ randperm(100), 102]; 24 temp = 0; 25 for i = 1 : 101 26 temp = temp + d(S(i), S(i + 1)); 27 end 28 if temp < Sum 29 S0 = S; Sum = temp; 30 end 31 end
求解过程:
(1)解空间
解空间S可表示为{1, 2, ..., 101, 102}的所有固定起点和终点的循环排列集合,即所有可能回路的集合。
(2)目标函数
路径长度最小
(3)产生新解(2变换法或3变换法)
(4)代价函数差 计算两种路径的路径差
(5)接受准则
若路径差小于0,则接受新的路径,否则以一定概率接受新的路径。
1 e = 0.1^30; L = 20000; at = 0.999; T = 1;
(6)降温
T <—— αT,得到新的温度, 这里取α=0.999.
(7)结束条件
用选定的终止温度e= 10的-30次方,判断退火过程是否结束。若T < e, 算法结束,输出当前状态。
while(T > e) %产生新解 c = 2 + floor(100 * rand(1, 2)); s = sort(c); c1 = s(1); c2 = s(2); %计算代价函数值 df = d(S0(c1-1),S0(c2)) + d(S0(c1),S0(c2+1)) - d(S0(c1-1),S0(c1)) - d(S0(c2),S0(c2+1)); %接受准则 if df < 0 || exp(-df / T) > rand(1) S0 = [S0(1:c1 - 1), S0(c2:-1:c1), S0(c2+1:102)]; Sum = Sum + df; end T = T * at; end
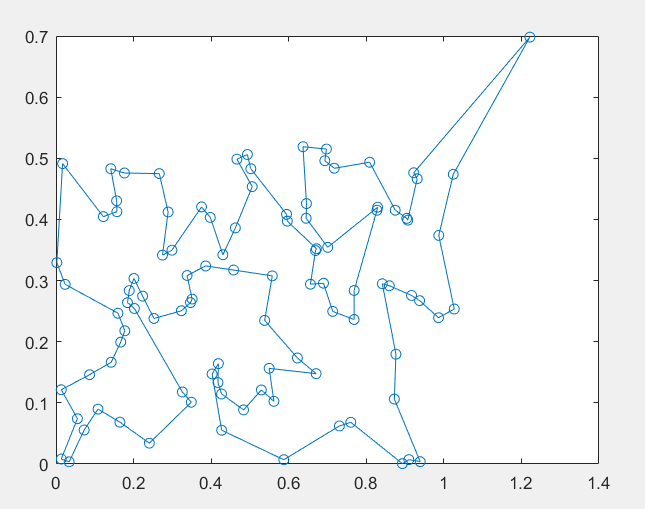
画出图象:
xx=sj(S0,1);
yy=sj(S0,2);
plot(xx,yy,'-o')