题目:
分析:
明确题意:在一棵树上给定若干权值为 (w) 的路径 ((u,v)) (盘子),每次给定 ((a,b)) (水果),询问所有满足 ((u,v)) 被 ((a,b)) 完全覆盖的路径中第 (k) 小的路径的权值。
先考虑如何快速判断 ((u,v)) 是不是 ((a,b)) 的子路径。第一反应是充要条件是 (a) 和 (b) 分别在 (u) 和 (v) 的子树中(设 (mathrm{dfn}_p) 是 (p) 在 dfs 序中的位置,以下默认 (mathrm{dfn}_u<mathrm{dfn}_v) 且 (mathrm{dfn}_a<mathrm{dfn}_b) )。这对于大部分情况是成立的,但是当 (u) 是 (v) 的祖先时并不成立,因为 (v) 的子树被包含在 (u) 的子树中,所以而在 (v) 的子树中任选两点都满足条件,但之间的路径并不能覆盖 ((u,v)) 。画图可知,此时 (b) 仍要求在 (v) 的子树中,而 (a) 应当在 (p) 的子树外(注意不是 (u) 的子树),其中 (p) 是从 (u) 到 (v) 的路径上除 (u) 之外的第一个点。详见下图(博客特色画风):
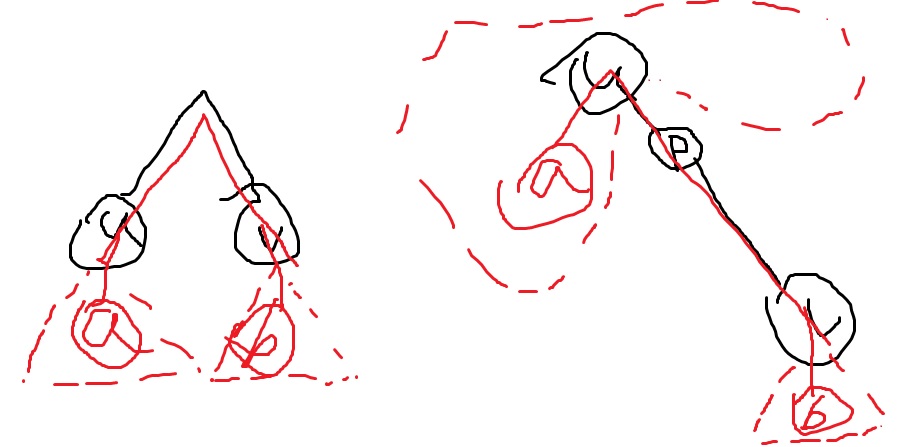
总结一下,如果 ((u,v)) 被 ((a,b)) 完全覆盖,那么需要满足:
如果 ((u,v)) 不是一条深度递增的链,那么需要满足( (mathrm{out}_p) 表示 (p) 的子树中最大的 (mathrm{dfn}) ):
否则需要满足( (p) 的含义见上):
对于求第 (k) 小的题,一个很常见的策略是二分。二分一个答案 (x) ,把所有权值小于等于 (x) 的点都插入数据结构,然后查询符合要求的点的数量,若大于等于 (k) 则向下二分,否则向上二分。
对于这道题,由于限制是二维的,所以需要树套树。插入一个路径 ((u,v)) 相当于给它能贡献到的地方的答案全部加 1 。对于 (u) 不是 (v) 的祖先的情况,这个「地方」是一维范围为 ([mathrm{dfn}_u,mathrm{out}_u]) ,另一维范围为 ([mathrm{dfn}_v,mathrm{out}_v]) 的矩形;否则,贡献到的是两个矩形(自行根据上面的式子构造)。查询一个路径 ((a,b)) 相当于查询点 ((mathrm{dfn}_a,mathrm{dfn}_b)) 的权值。由于是多组询问,所以套上整体二分,时间复杂度 (O(nlog^3 n)) 。
然而实测树套树会不幸被 卡常 卡复杂度。可以用类似离线扫描线的思想,把修改和询问按第一维的 dfn 排序,然后按 dfn 从小到大处理,并把修改拆成两次: 在 (mathrm{dfn}_u) 处给 ([mathrm{dfn}_v,mathrm{out}_v]) 加 1 ,在 (mathrm{out}_u+1) 处给上述区间减 1 。用树状数组维护区间修改和单点查询,时间复杂度 (O(nlog^2 n)) 。
代码:
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
namespace zyt
{
template<typename T>
inline bool read(T &x)
{
char c;
bool f = false;
x = 0;
do
c = getchar();
while (c != EOF && c != '-' && !isdigit(c));
if (c == EOF)
return true;
if (c == '-')
f = true, c = getchar();
do
x = x * 10 + c - '0', c = getchar();
while (isdigit(c));
if (f)
x = -x;
return true;
}
template<typename T>
inline void write(T x)
{
static char buf[20];
char *pos = buf;
if (x < 0)
putchar('-'), x = -x;
do
*pos++ = x % 10 + '0';
while (x /= 10);
while (pos > buf)
putchar(*--pos);
}
const int N = 4e4 + 10, B = 16;
int n, head[N], ecnt, fa[N][B], dep[N], dfn[N], dfncnt, out[N], id[N], ans[N];
struct edge
{
int to, next;
}e[N << 1];
struct _plt
{
int u, v, c, nxt;
bool operator < (const _plt &b) const
{
return c < b.c;
}
}plt[N]; // plate
int idplt[N];
struct _frt
{
int u, v, k, id;
}frt[N]; // fruit
bool cmpdfnu(const int a, const int b)
{
return dfn[frt[a].u] < dfn[frt[b].u];
}
namespace Tree_Array
{
int data[N];
inline int lowbit(const int x)
{
return x & (-x);
}
void add(int a, const int x)
{
while (a <= n)
data[a] += x, a += lowbit(a);
}
int query(int a)
{
int ans = 0;
while (a)
ans += data[a], a -= lowbit(a);
return ans;
}
void add(const int l, const int r, const int x)
{
add(l, x), add(r + 1, -x);
}
}
void add(const int a, const int b)
{
e[ecnt] = (edge){b, head[a]}, head[a] = ecnt++;
}
void dfs(const int u, const int f)
{
fa[u][0] = f;
for (int i = 1; i < B; i++)
fa[u][i] = fa[fa[u][i - 1]][i - 1];
dep[u] = dep[f] + 1;
dfn[u] = ++dfncnt;
for (int i = head[u]; ~i; i = e[i].next)
{
int v = e[i].to;
if (v == f)
continue;
dfs(v, u);
}
out[u] = dfncnt;
}
inline int lca(int a, int b)
{
if (dep[a] < dep[b])
swap(a, b);
for (int i = B - 1; i >= 0; i--)
if (dep[fa[a][i]] >= dep[b])
a = fa[a][i];
if (a == b)
return a;
for (int i = B - 1; i >= 0; i--)
if (fa[a][i] != fa[b][i])
a = fa[a][i], b = fa[b][i];
return fa[a][0];
}
namespace Divide_Together
{
struct _mdf
{
int pos, l, r, x;
_mdf() {}
_mdf(const int _pos, const int _l, const int _r, const int _x)
: pos(_pos), l(_l), r(_r), x(_x) {}
bool operator < (const _mdf &b) const
{
return pos < b.pos;
}
}mdf[N << 1];
int cnt;
void insert(const int l, const int r, const int ll, const int rr, const int x)
{
mdf[cnt++] = _mdf(l, ll, rr, x);
mdf[cnt++] = _mdf(r + 1, ll, rr, -x);
}
void insert(const int i, const int x)
{
if (plt[i].nxt)
{
insert(1, dfn[plt[i].nxt] - 1, dfn[plt[i].v], out[plt[i].v], x);
if (out[plt[i].nxt] < n)
insert(dfn[plt[i].v], out[plt[i].v], out[plt[i].nxt] + 1, n, x);
}
else
insert(dfn[plt[i].u], out[plt[i].u], dfn[plt[i].v], out[plt[i].v], x);
}
void solve(const int l, const int r, const int ql, const int qr)
{
using Tree_Array::query;
using Tree_Array::add;
if (l == r)
{
for (int i = ql; i <= qr; i++)
ans[frt[id[i]].id] = plt[l].c;
return;
}
static int buf1[N], buf2[N];
int cnt1 = 0, cnt2 = 0;
int mid = (l + r) >> 1;
cnt = 0;
for (int i = l; i <= mid; i++)
insert(i, 1);
sort(mdf, mdf + cnt);
int now = 0;
for (int i = ql; i <= qr; i++)
{
while (now < cnt && mdf[now].pos <= dfn[frt[id[i]].u])
add(mdf[now].l, mdf[now].r, mdf[now].x), ++now;
int tmp = query(dfn[frt[id[i]].v]);
if (tmp >= frt[id[i]].k)
buf1[cnt1++] = id[i];
else
buf2[cnt2++] = id[i], frt[id[i]].k -= tmp;
}
for (int i = 0; i < cnt1; i++)
id[i + ql] = buf1[i];
for (int i = 0; i < cnt2; i++)
id[i + cnt1 + ql] = buf2[i];
for (int i = 0; i < now; i++)
add(mdf[i].l, mdf[i].r, -mdf[i].x);
solve(l, mid, ql, ql + cnt1 - 1);
solve(mid + 1, r, ql + cnt1, qr);
}
}
int work()
{
int p, q;
read(n), read(p), read(q);
memset(head, -1, sizeof(int[n + 1]));
for (int i = 1; i < n; i++)
{
int a, b;
read(a), read(b);
add(a, b), add(b, a);
}
dfs(1, 0);
for (int i = 0; i < p; i++)
{
read(plt[i].u), read(plt[i].v), read(plt[i].c);
if (dfn[plt[i].u] > dfn[plt[i].v])
swap(plt[i].u, plt[i].v);
plt[i].nxt = 0;
if (lca(plt[i].u, plt[i].v) == plt[i].u)
{
int &tmp = plt[i].nxt;
tmp = plt[i].v;
for (int j = B - 1; j >= 0; j--)
if (dep[fa[tmp][j]] > dep[plt[i].u])
tmp = fa[tmp][j];
}
}
sort(plt, plt + p);
for (int i = 0; i < q; i++)
{
id[i] = i;
read(frt[i].u), read(frt[i].v), read(frt[i].k);
if (dfn[frt[i].u] > dfn[frt[i].v])
swap(frt[i].u, frt[i].v);
frt[i].id = i;
}
sort(id, id + q, cmpdfnu);
Divide_Together::solve(0, p - 1, 0, q - 1);
for (int i = 0; i < q; i++)
write(ans[i]), putchar('
');
return 0;
}
}
int main()
{
return zyt::work();
}