更新记录
【1】2020.05.09-13:28
1.完善内容
【2】2020.07.18-09:11
1.更改了一个小小的错误
正文
观前提示
- 此文章为重温系列,并不会讲的很细致
- 需要有一定高精度与排序基础
高精度
前言
高精度说实话是好久没打了,不是因为我没时间刷题,而是因为我懒
高精度这个东西考察的就是细心,一点错,满盘皆输
(对没错这就是我一般不刷高精度的原因)
所有代码均经过压行与评测处理,请放心食用
减法为加法的逆运算,除法为乘法的逆运算,所以不贴这两个高精度的代码
高精度加法
- 倒序存储
- 按位加,考虑进位
- (ans[i]=a[i]+b[i])
- (ans[i+1]=(a[i]+b[i])/10)
- (ans[i]=(a[i]+b[i])\%10)
- 输出
本代码用了玄学的进位处理,不要效仿
#include<iostream>
using namespace std;
string a,b;
int c[10001],d[10001],e[10001];
bool ba;
int main()
{
int js=0,we=0;
cin>>a>>b;
for(int i=0;i<a.length();i++)
c[i]=a[a.length()-i-1]-'0';
for(int i=0;i<b.length();i++)
d[i]=b[b.length()-i-1]-'0';
for(int i=0;i<max(a.length(),b.length());i++){
if(i>=min(a.length(),b.length())){
if(a.length()>b.length()) e[we]=e[we]+c[i];
else e[we]=e[we]+d[i];
}
else
e[we]=c[i]+d[i];
if(e[we-1]>=10)
e[we-1]%=10;e[we]+=1;
we+=1;
}
for(int i=we-1;i>=0;i--){
if(!e[i]&&!ba) continue;
else ba=1;
cout<<e[i];
}
}
高精度减法
- 倒序存储
- 按位减,考虑退位
- 输出
和加法一样就不写太多了
高精度乘法
计算的时候把大数放在前面会得到无限的便利
至于是什么便利就交给你们去发现了
没错我们先倒序存储
然后我们自己在草稿纸上演算,别忘记中间过程也要倒序处理
然后就是这么个效果

1234*567=699678
这么一观察我们就能发现突破口
定义两层循环,按位乘
最后加起来。。。?
要不要补零啊
不需要
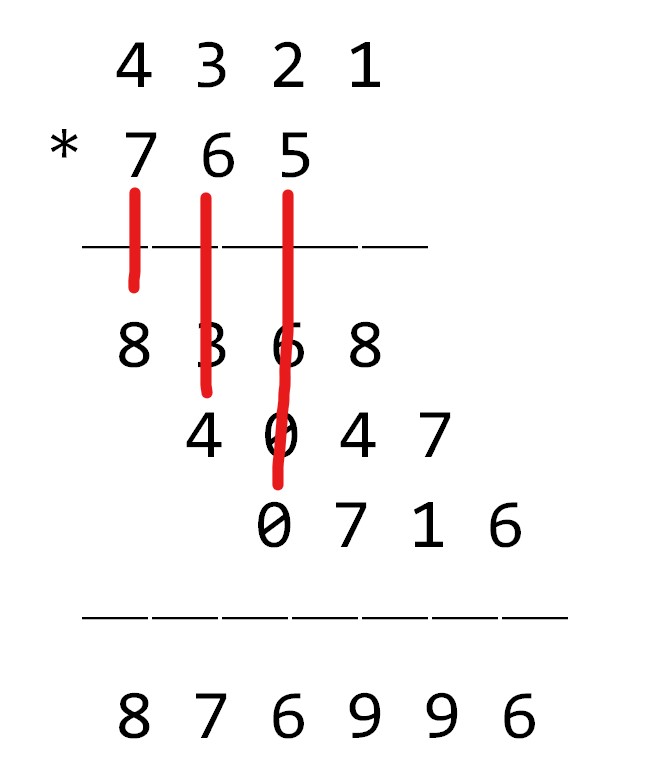
我们发现这都是一一对应的,循环的时候控制一下就可以了
看错范围差点去写FFT
有些人会发现我码风变了,原因是被Java带的QAQ
#include<iostream>
using namespace std;
string a,b;
bool ba;
int c[1001],d[1001],e[100001],la,lb;
void cmp1(){
if(a.length()==b.length()){
for(int i=0;i<a.length();i++){
if(a[i]<b[i]) {swap(a,b);return;}
}
}
else{
if(a.length()<b.length())
swap(a,b);
}
}
int main(){
cin>>a>>b;cmp1();
la=a.length()-1,lb=b.length()-1;
for(int i=la;i>=0;i--) c[la-i+1]=a[i]-'0';
for(int i=lb;i>=0;i--) d[lb-i+1]=b[i]-'0';
for(int i=1;i<=b.length();i++){
for(int o=1;o<=a.length();o++){
e[i+o-1]+=(d[i]*c[o]+e[i+o-2]/10);
e[i+o-2]%=10;
}
if(e[i+la]>9){
e[i+la+1]+=(e[i+la]/10);
e[i+la]%=10;
}
}
for(int i=la+lb+2;i>0;i--){
if(!ba&&!e[i]) continue;
else ba=1;
cout<<e[i];
}
}
高精度除法
每一位进行加法逼近,然后来次高精减
一直算到最后一位即可
排序
快速排序
这里主要写sort函数
函数用法(已简化):(sort(begin,end,cmp);)
begin默认从零开始,所以要想排1~N begin应该+1
cmp就是自定义排序函数
cmp的实参的类型与要排序的数组的类型一样
注意:结构体排序必须写cmp,否则报错
二路归并排序
- 代码我用回车分为三部分
void msort(int s,int e){
if(s==e) return;
long long int mid=(s+e)/2;
msort(s,mid);msort(mid+1,e);
int i=s,j=mid+1,k=s;
while(i<=mid&&j<=e){
if(a[i]<=a[j]) {r[k]=a[i];k+=1;i+=1;}
else {r[k]=a[j];k+=1;j+=1;}
}
while(i<=mid) {r[k]=a[i];k+=1;i+=1;}
while(j<=e) {r[k]=a[j];k+=1;j+=1;}
for(int i=s;i<=e;i++)
a[i]=r[i];
}
第一部分
判断与定义变量部分
if(s==e) return;:开头和结尾一样 = 只有一个数 = 直接跳出,不需要任何操作long long int mid=(s+e)/2;int i=s,j=mid+1,k=s;:定义mid,值为s与e的平均数(分治的标志),顺便我们备份一下开头和结尾,现在定义j将s至e分为两个区间:s - mid , mid+1 - e,也就是:i - mid , j - e- 先让左右区间分解,合并:
msort(s,mid);msort(mid+1,e);
第二部分
左右区间的合并
- 由于左右区间经过第一部分的操作,已经为有序区间,所以这两个区间开头的数必为区间最大(小)值,我们只要判断开头就可以了(这里以从小到大排列为例)
- 哪边小,就将其加到另一个数组中(为了不破坏原数组),然后相应的区间端点+1(这个数判断完了就要从下一个开始,由于是从端点开始判断(端点开始是因为有序性,上文已经提及),就相当于缩小区间)
- 以此类推,直到一边判断完毕
- 此时原数组依然可能有残留的数,例如({1,2,3,4})与({5,6,7,8})这两个区间
- 这时我们通过两个循环来清除
- 那么为什么要写在一起而不判断情况呢,我们可以进行一个小小的证明(真的很小QAQ)
-
- 由于一个区间已经复制完毕,所以必有一个区间长度为0
while(i<=mid&&j<=e){
//起始点等于结束点的时候,循环依然成立,此时长度为1
if(a[i]<=a[j]) {r[k]=a[i];k+=1;i+=1;}
//这两个
else {r[k]=a[j];k+=1;j+=1;}
//必会执行一个,导致起始点+1,此时起始点=结束点+1
}
所以这两个while循环只会执行一个
第三部分
数组的复制
你都归并好了你不复制回去嘛
堆排序
建个小根(大根)堆就排好了
void put(int a){
int now,next;hs+=1;
h[hs]=a;now=hs;
while(now>1){
next=now>>1;
if(h[now]>=h[next])
break;
swap(h[now],h[next]);
now=next;
}
}
一次插入时间复杂度为(O(logn))
总复杂度为(O(nlogn))
并且时间复杂度比较稳定
实战
以下是我通过TLE换来的教训
- 不一定什么都要用高精去和另一个高精去加,去乘
- 同样的,不一定什么都要按位,有时候我们可以直接压位计算,即将一个多位数看成一位数
例如这道题:
任意给定一个正整数N(N≤100),计算2的n次方的值。
#include<iostream>
using namespace std;
int a[1001],cnt,times;
int jie(int num){
for(int i=0;i<num;i++){
for(int o=0;o<cnt;o++){
if(a[o]>9)
if(o==cnt-1)
cnt+=1;
a[o]*=2;
if(a[o-1]>9&&o)
a[o-1]-=10;a[o]+=1;
if(o==cnt-1)
if(a[o]>9){
cnt+=1;a[o]-=10;a[o+1]+=1;
break;
}
}
}
}
int main(){
a[0]=1;cnt=1;
cin>>times;jie(times);
for(int i=cnt-1;i>=0;i--)
cout<<a[i];
}
这个其实就是一个初级应用
再看一个例子
求10000以内n的阶乘。
这个题就需要一定技巧了,暴力的结果只能是TLE
(还有Wonderful Answer呢awa)
例如最后一步:*10000
- 这个时候我们就要把10000看成一个数,一起乘进去
- 最后处理进位
单单*10000这一步,时间复杂度就变为了原来的1/5
那么整道题基本可以达到暴力的1/3 - 1/4倍的时间复杂度
不贴代码了你自己做去awa
总结
- 高精度与排序都是比较基础的内容,比赛一般不会单独拿出来考
- 这更需要我们牢牢掌握它
不要以为简单就不去练习,基础的内容更需要我们经常复习
