算法初探

更新记录

【1】2020.10.18-16:34

• 1.初步的写了写

目录

• 可持久化数组
• 可持久化线段树（咕咕咕）
• 可持久化平衡树（咕咕咕）
• 可持久化并查集（咕咕咕）

正文

可持久化这个东西啊，简单的来说就是增加题目难度通过奇妙的方式新建结点来保存之前的信息，以达到回退的目的

可持久化数组

数组是我们经常接触的东西

但是一可持久化就成蓝题了

这其实相当于单点修改单点查询的主席树

我们会发现一次操作最多更新 (lg n) 个节点

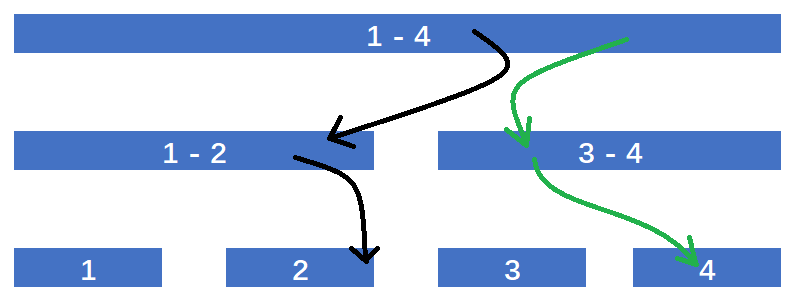
于是我们把这 (lg n) 个节点存一下即可

那么怎么存呢？

对于update（change）在每层递归的时候新建结点就可以

对于query直接复制

最后把根节点存一下即可

【代码实现】

#include<iostream>
#define fx(l,n) inline l n
#define N 14000001
using namespace std;
int v[N],n,m,ver,op,loc,val,root[N],node=1;
struct PT{
	int l,r,v;
}t[N];
fx(void,build)(int p,int l,int r){
	if(l==r){
		t[p].v=v[l];
		return;
	}
	int mid=(l+r)>>1;
	t[p].l=++node;
	build(t[p].l,l,mid);
	t[p].r=++node;
	build(t[p].r,mid+1,r);
}
fx(int,newnd)(int p){
	t[++node]=t[p];
	return node;
}
fx(int,change)(int p,int l,int r,int pl,int v){
	p=newnd(p);
	if(l==r){
		t[p].v=v;
	} else{
		int mid=(l+r)>>1;
		if(pl<=mid) t[p].l=change(t[p].l,l,mid,pl,v);
		else t[p].r=change(t[p].r,mid+1,r,pl,v);
	}
	return p;
}
fx(int,query)(int p,int l,int r,int pl){
	if(l==r){
		return t[p].v;
	} else{
		int mid=(l+r)>>1;
		if(pl<=mid) return query(t[p].l,l,mid,pl);
		else return query(t[p].r,mid+1,r,pl);
	}
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>v[i];
	build(1,1,n);
	root[0]=1;
	for(int i=1;i<=m;i++){
		cin>>ver>>op>>loc;
		if(op==1){
			cin>>val;
			root[i]=change(root[ver],1,n,loc,val);
		} else{
			cout<<query(root[ver],1,n,loc)<<"
";
			root[i]=root[ver];
		}
	}
}