CSP-S2020解题报告

目录

• T1.儒略日
• T2.动物园
• T3.函数调用
• T4.贪吃蛇

T1.儒略日

没啥好说的，按题面描述模拟就行

分成三类：公元前，1582.10.4（含）前，和1582.10.15（含）后

#include<iostream>
#include<fstream>
#include<cstdio>
#include<cstring>
#define int long long
#define N 1000001
#define fx(l,n) inline l n
#define set(l,n) memset(l,n,sizeof(l))
using namespace std;
int n,t,ct,now,m[13]={0,31,29,31,30,31,30,31,31,30,31,30,31},D,M,Y;
int F[5]={0,366,365,365,365};
bool beaf;
fx(void,work)(int t,bool y){
	if(!y) m[2]-=1;
	for(int i=1;i<=12;i++){
		if(t>=m[i]){
			t-=m[i];
		} else {
			M=i;D=t+1;
			break;
		}
	}
	if(!y) m[2]+=1;
}
fx(bool,pan)(int a){
	if(a%4==0){
		if(a%100==0){
			if(a%400==0) return 1;
			else return 0;
		}
		return 1;
	}
	return 0;
}
signed main(){
	cin>>n;
	while(n--){
		cin>>t;ct=t;beaf=0;
		if(t>=1721424){
			t-=1721424;
			if(t>=577738) t+=10;
			if(t>=578122){
				ct=t;
				t/=1461;
				if(t<=400){
					ct-=t*1461;
					Y=t*4+1;
				} else {
					t=ct;t-=(400*1461);ct=t;
					Y=1601;
					t/=146097;
					ct-=t*146097;
					Y+=t*400;
				}
				for(int i=1;i<=400;i++){
					if(ct>=(365+pan(i))){
						ct-=(365+pan(i));
						Y+=1;
					} else {
						work(ct,pan(i));
						break;
					}
				}
			} else {
				ct=t;t/=1461;
				Y=4*t+1;
				ct-=t*1461;
				for(int i=4;i>=1;i--){
					if(ct>=F[i]){
						ct-=F[i];
						Y+=1;
					} else {
						work(ct,i==1);
						break;
					}
				}
			}
		} else {
			beaf=1;
			t/=1461;
			Y=4713-4*t;
			ct-=t*1461;
			for(int i=1;i<=4;i++){
				if(ct>=F[i]){
					ct-=F[i];
					Y-=1;
				} else {
					work(ct,i==1);
					break;
				}
			}
		}
		cout<<D<<" "<<M<<" "<<Y<<(beaf?" BC
":"
");
	}
	return 0;
}

T2.动物园

一眼水题

对于每个已经有的二进制位统计要买的饲料

然后循环一遍规则

确定哪些没有的二进制位满足条件，即不需要购买额外的饲料

每个满足条件的二进制位可以对已有的答案产生*2的贡献

统计即可

#include<iostream>
#include<fstream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 1000010
#define int unsigned long long
#define fx(l,n) inline l n
#define set(l,n) memset(l,n,sizeof(l))
using namespace std;
int cnt[N],v[N],num,pl[N],zh[N],zhong=1,ans=1,n,m,c,k,cp[N],pla;
bool z[N],able[N];
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>c>>k;
	for(int i=1;i<=n;i++){
		cin>>v[i];num=0;
		while(v[i]){
			if(v[i]&1) cnt[num]+=1;
			v[i]>>=1;
			num+=1; 
		}
	}
	for(int i=1;i<=m;i++){
		cin>>pl[i]>>zh[i];
		cp[i]=zh[i];
	}
	sort(cp+1,cp+m+1);
	pla=unique(cp+1,cp+m+1)-cp;
	for(int i=1;i<=m;i++){
		zh[i]=lower_bound(cp+1,cp+pla,zh[i])-cp;
		if(cnt[pl[i]]) z[zh[i]]=1;
	}
	for(int i=0;i<k;i++) able[i]=1;
	for(int i=1;i<=m;i++){
		if((!cnt[pl[i]])&&(!z[zh[i]])) able[pl[i]]=0;
	}
	for(int i=0;i<k;i++) if(able[i]) ans<<=1;
	if(k==64&&n==0&&m==0) cout<<"18446744073709551616";
	else cout<<ans-n;
	return 0;
}

T3.函数调用

还是有些思维含量的题

我们可以直接倒序处理

即一个数 (c) 对于两个操作：+a *b

由乘法分配律得：((c+a)*b=c*b+a*b)

所以统计到现在为止的乘法系数，对于一个加法操作直接乘这个系数相加即可

对于乘法操作直接全局统计

对于依次调用的暴力展开

可以获得 (75pts) 的好成绩

以下均为倒序处理

考虑优化，我们发现对于一个函数我们重复计算了多次

怎么一次将其所做的贡献计算完毕呢？

我们发现对于一个依次调用的函数

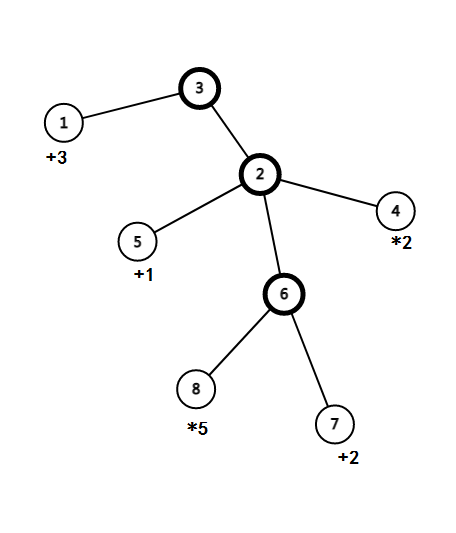
（加粗的表示依次调用的函数）

这时候就需要线段树的标记下传思想，将每个函数 (i) 对应一个加法系数 (mul[i])

预处理出每个函数所能贡献的乘法倍率

我们按照拓扑序处理

看这张图，首先处理3号函数，然后因为是倒序处理，并且2号函数也是个递归调用的函数，不管

然后是1号函数的+1操作，它所做的贡献是本身的加数值乘以2号函数所贡献的乘法倍率，即 (3*10=30)

然后依照拓扑序，处理2号函数

首先是4号函数的*2，累计

然后是6号函数，然后将6号函数的加法系数加上2

然后是5号函数的+1，它所做的贡献是本身的加数值乘以6号函数和2号函数内部之前的乘法操作所贡献的乘法倍率，即 (1*2*5=10)

最后是6号函数，依照之前的处理即可

正确性：对于调用 (i) 号函数的两个函数 (a,b)，这两个函数对于 (i) 号函数中的一个加法操作+c的乘法倍率分别是 (mul_a,mul_b)

于是乎两次贡献的就是 (c*mul_a+c*mul_b=c*(mul_a+mul_b))

最后的答案可以转化为乘上函数内乘法所做的贡献然后加上函数内加法所做的贡献

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<algorithm>
#define N 1000001
#define int long long
#define fx(l,n) inline l n
#define set(l,n) memset(l,n,sizeof(l))
using namespace std;
const int mod=998244353;
int n,v[N],mul[N],num,Fa[N],pl[N],op[N],size,h,deal,doing[N],mult=1,sumul[N],in[N],tp[N];
bool bl;
vector<int>f[N];
queue<int>q;
fx(void,tpsort)(){
	for(int i=1;i<=num;i++) if(!in[i]) q.push(i);
	h=0;
	int n;
	while(q.size()){
		n=q.front();q.pop();
		tp[++h]=n;
		for(int i=0;i<f[n].size();i++){
			in[f[n][i]]-=1;
			if(!in[f[n][i]]) q.push(f[n][i]);
		}
	}
}
fx(void,askmul)(int a){
	mul[a]=1;
	for(int i=0;i<f[a].size();i++){
		if(mul[f[a][i]]==-1) askmul(f[a][i]);
		(mul[a]*=mul[f[a][i]])%=mod;
	}
}
fx(void,pushdown)(){
	for(int i=1;i<=num;i++){
		mult=1;
		for(int o=f[tp[i]].size()-1;o>=0;o--){
			(sumul[f[tp[i]][o]]+=sumul[tp[i]]*mult)%=mod;
			(mult*=mul[f[tp[i]][o]])%=mod;
		}
	}
}
fx(void,compute)(){
	for(int i=1;i<=num;i++)
		if(op[i]==1)
			(v[pl[i]]+=sumul[i]*Fa[i]%mod)%=mod;
}
signed main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>v[i];
	cin>>num;
	for(int i=1;i<=num;i++){
		cin>>op[i];
		if(op[i]==1){
			cin>>pl[i]>>Fa[i];mul[i]=1;
		} else if(op[i]==2) {
			cin>>mul[i];
		} else {
			cin>>size;mul[i]=-1;
			for(int o=1;o<=size;o++){
				cin>>h;f[i].push_back(h);in[h]+=1;
			}
		}
	}
	for(int i=1;i<=num;i++){
		if(~mul[i]) continue;
		askmul(i);
	}
	cin>>deal;
	for(int i=1;i<=deal;i++) cin>>doing[i];
	for(int i=deal;i>=1;i--){
		(sumul[doing[i]]+=mult)%=mod;
		(mult*=mul[doing[i]])%=mod;
	}
	for(int i=1;i<=n;i++) (v[i]*=mult)%=mod;
	tpsort();
	pushdown();
	compute();
	for(int i=1;i<=n;i++) cout<<v[i]%mod<<" ";
}

T4.贪吃蛇

神仙博弈，考虑两种情况：

Case 1：吃之后不是最弱的，此时吃完之后肯定有蛇垫背，必吃
Case 2：吃之后是最弱的，接着递归，考虑奇偶性即可

因为自己太弱了就只能仿着题解调

#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 1500001
#define fx(l,n) inline l n
#define set(l,n) memset(l,n,sizeof(l))
int v[N],p,val,t,n,ans,ma,mi,cp[N],own[N],die[N],cn;
struct queue{
	int v[N],h,t;
	fx(void,todo)(int he,int ta){h=he,t=ta;}
}q1,q2;
fx(int,read)(){
	int x =0; char c =getchar();
	while(c < '0' || c > '9') c =getchar();
	while(c >= '0' && c <= '9') x =(x<<1)+(x<<3)+(48^c), c =getchar();
	return x;
}
fx(int,smax)(int a,int b){
	if(a==0||b==0) return a?a:b;
	if(cp[a]==cp[b]) return b>a?b:a;
	else return cp[a]>cp[b]?a:b;
}
fx(int,smin)(int a,int b){
	if(a==0||b==0) return a?a:b;
	if(cp[a]==cp[b]) return b<a?b:a;
	else return cp[a]<cp[b]?a:b;
}
fx(int,judge)(int a,int b){
	for(int i=a;i>=0;i--)
		if(b>die[own[i]])
			b=i;
	return b;
}
signed main(){
	t=read();
	for(int i=1;i<=t;i++){
		n=read();
		if(i==1){
			cn=n;for(int o=1;o<=n;o++) v[o]=read();
		} else {
			for(int o=1;o<=n;o++){
				p=read();val=read();v[p]=val;
			}
		}
		memcpy(cp,v,sizeof(v));
		for(int o=1;o<=cn;o++) q1.v[cn-o+1]=o;
		set(q2.v,0);set(die,0x3f);set(own,0);
		q1.todo(1,cn);q2.todo(1,0);
		ans=0;
		for(int o=0;o<cn-1;o++){
			ma=smax(q1.v[q1.h],q2.v[q2.h]);
			mi=smin(q1.v[q1.t],q2.v[q2.t]);
			if(ma==q1.v[q1.h]) q1.v[q1.h++]=0;
			else q2.v[q2.h++]=0;
			if(mi==q1.v[q1.t]) q1.v[q1.t--]=0;
			else q2.v[q2.t--]=0;
			own[o]=ma;die[mi]=o;cp[ma]-=cp[mi];
			if(o==cn-2){
				ans=judge(o-1,o+1);
				break;
			} else if(q2.t>=q2.h&&smin(q2.v[q2.t],ma)!=ma) {
				ans=judge(o-2,o-1);
				break;
			}
			q2.v[++q2.t]=ma;
		}
		printf("%d
",cn-ans);
	}
}