zoukankan html css js c++ java

爆零后的感受外加一道强联通分量HDU 4635的题解

今天又爆零了，又是又，怎么又是又，爆零爆多了，又也就经常挂嘴边了，看到这句话，你一定很想说一句””，弱菜被骂傻，也很正常啦。

如果你不开心，可以考虑往下看。

翻到E（HDU 4635 Strongly connected）题，这么短的题目，肯定要先看啦。然后D（LightOJ 1229），然后C（ZOJ 2243），然后F(HDU 4711),然后B（CodeForces 385D），然后看A（HDU 3889）好吧，我承认，A题看了一眼就不看了，B题一看是线段什么有点几何的味道就果断放弃，然后C题，傻傻的理解错题意，提交一直WA，然后没办法，看E题，想到只要保证最后至少两个连通分量，就可以满足题意，然后要求最大值，那就保证有且仅有两个连通分量就可以了，对于一个连通分量最多只能有x(x-1)边, x表示顶点数，然后得出一个式子，边数f = n*n-n-1+x*x-(n+1)x;当x更(n+1)/2的差值越大，f越大，换句话说，只要把一个连通分量顶点个数最小的独立出来，把其它的连通分量都合并成一个连通分量就可以了，

可是我没考虑下面这种情况

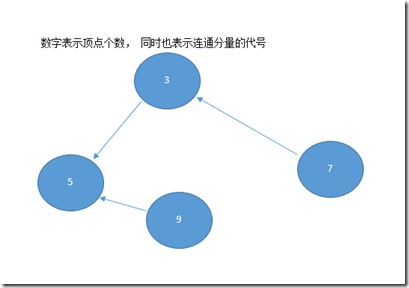
这时候如果把3独立出来，5、9、7弄成一个连通分量，那么3也会跟5，9，7合并成一个连通分量，所以不能选3，

最小的不能选，那就选5吧，把3、7、9合并，可以。

也就是说是要把顶点个数尽量小且入度或者初度为零（一个连通分量看成一个点）的连通分量独立出来。

view code#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cmath>
#include <vector>
#include <map>
#include <stack>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int N = 100010;
int _, cas=1, n, m;
int in[N], out[N], num[N];

vector<int > G[N];
int pre[N], lowlink[N], dfs_clock, scc_cnt, sccno[N];
stack<int >S;

void dfs(int u)
{
    pre[u] = lowlink[u] = ++dfs_clock;
    S.push(u);
    int siz = G[u].size();
    for(int i=0; i<siz; i++)
    {
        int v = G[u][i];
        if(!pre[v])
        {
            dfs(v);
            lowlink[u] = min(lowlink[u], lowlink[v]);
        }
        else if(!sccno[v])
        {
            lowlink[u] = min(lowlink[u], pre[v]);
        }
    }
    if(lowlink[u] == pre[u])
    {
        scc_cnt++;
        for(;;)
        {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            num[scc_cnt]++;
            if(x==u) break;
        }
    }
}

void find_scc()
{
    dfs_clock = 0;
    scc_cnt = 0;
    memset(sccno, 0, sizeof(sccno));
    memset(pre, 0, sizeof(pre));
    for(int i=1; i<=n; i++)
    {
        if(!pre[i]) dfs(i);
    }
}

void solve()
{
    scanf("%d%d", &n ,&m);
    memset(num, 0, sizeof(num));
    memset(in, 0, sizeof(in));
    memset(out, 0, sizeof(out));
    for(int i=1; i<=n ;i++) G[i].clear();

    int u, v;
    for(int i=0; i<m; i++)
    {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
    }
    find_scc();
    printf("Case %d: ", cas++);
    if(scc_cnt==1)
    {
        printf("-1
");
        return ;
    }
    ll ans = 0, Min = INF;
    for(int i=1; i<=n; i++)
    {
        int siz = G[i].size();
        for(int j=0; j<siz; j++)
        {
            if(sccno[i]!=sccno[G[i][j]])
            {
                in[sccno[G[i][j]]]++;
                out[sccno[i]]++;
            }
        }
    }
    for(int i=1; i<=scc_cnt; i++)
    {
        if((in[i]==0 || out[i]==0)  && Min>num[i]) Min = num[i];
//        printf("num[%d] = %d
", i, num[i]);
//        printf("out = %d, in = %d
", out[i], in[i]);
    }
    ans  = (Min-1)*Min- m + (n-Min)*(n-Min-1)+Min*(n-Min);
    cout<<ans<<endl;
}

int main()
{
//    freopen("in", "r", stdin);
    cin>>_;
    while(_--) solve();
    return 0;
}

红色部分就是思维漏洞

。差一点，不过acm没有差一点，只有ac或者没ac. $06XAV{(MDKRWX3~JPUBND_U$

下面再来总结一下题目吧
Problem A
HDU 3889（水题，不会做）

Problem B
CodeForces 385D（dp,题意尚不明确）

Problem C
ZOJ 2243（什么treap,被坑）

笛卡尔树：

　　每个节点有2个关键字key、value。从key的角度看，这是一颗二叉搜索树，每个节点的左子树的key都比它小，右子树都比它大；从value的角度看，这是一个堆。

题意：以字符串为关键字key，数字为关键字value，构造一个二叉搜索大堆，最后按要求中序遍历笛卡尔树的构造。

view code#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int N = 55555;
const int INF = 1<<30;
int n, pos[N<<2], Max[N<<2];

struct node
{
    char str[55];
    int data;
    bool operator < (const node &o) const{
        return strcmp(str,o.str)<0;
    }
}sto[N];

void Up(int rt)
{
    int ls = rt<<1, rs=ls|1;
    if(Max[rs]>Max[ls]) pos[rt] = pos[rs], Max[rt] = Max[rs];
    else pos[rt] = pos[ls], Max[rt] = Max[ls];
}

void build(int l, int r, int rt)
{
    if(l==r)
    {
        Max[rt] = sto[l].data;
        pos[rt] = l;
        return ;
    }
    int m = (l+r)>>1;
    build(lson);
    build(rson);
    Up(rt);
}

int query(int L, int R, int l, int r, int rt)
{
    if(L<=l && R>=r) return pos[rt];
    int m = (l+r)>>1;
    if(R<=m) return query(L, R, lson);
    if(L>m) return query(L, R, rson);
    int lpos = query(L, R, lson);
    int rpos = query(L, R, rson);
    return sto[lpos].data<sto[rpos].data?rpos:lpos;
}

void print(int l, int r)
{
    if(l>r) return ;
    if(l==r)
    {
        printf("(%s/%d)", sto[l].str, sto[l].data);
        return ;
    }
    int m = query(l, r, 0, n-1, 1);
    printf("(");
    print(l, m-1);
    printf("%s/%d", sto[m].str, sto[m].data);
    print(m+1,r);
    printf(")");
}

void solve()
{
    for(int i=0; i<n; i++)
    {
        scanf(" %[a-z]/%d", sto[i].str, &sto[i].data);//这个输入方式。。又涨姿势了
//        printf("%s/%d
", sto[i].str, sto[i].data);
    }
    sort(sto, sto+n);
    build(0, n-1, 1);
    print(0, n-1);
    printf("
");
}

int main()
{
//    freopen("in.txt", "r", stdin);
    while(scanf("%d", &n)>0 && n) solve();
    return 0;
}

//[a-z]表示读取的字符串由a-z中的字符组成，其余的字符为定界符scanf/fscanf 的%[]和%n使用方法

Problem D
LightOJ 1229（博弈,大白书P139）

view code#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 222;
int _, cas=1, n;
int sg[N] = {0, 1, 1, 1};
bool vis[N];
char s[N];

void init()
{
    int i, j;
    for(i=4; i<=200; i++)
    {
        memset(vis, 0, sizeof(vis));
        for(j=3; j<=5 && j<=i ; j++) vis[sg[i-j]] = 1;
        for(j=1; j+5<i; j++) vis[(sg[j]^sg[i-j-5])] = 1;
        for(j=0; ; j++) if(!vis[j]) break;
        sg[i] = j;
    }
//    for(int i=0;i <20; i++) printf("sg[%d] = %d
", i, sg[i]);
}

bool is_ok(int pos)
{
    if(pos>2 && s[pos-2]=='X' &&s[pos-1]=='X') return true;
    if(pos>1 && pos<n && s[pos-1]=='X' && s[pos+1]=='X') return true;
    if(pos<n-1 && s[pos+1]=='X' && s[pos+2] == 'X') return true;
    for(int k=pos-2; k<=n && k<=pos+2; k++)
    {
        if(k<1) continue;
        if(s[k]=='X') return 0;
    }
    return 1;
}

bool win(int pos)
{
    for(int i=3; i<=n; i++) if(s[i]=='X'&&s[i-1]=='X'&&s[i-2]=='X') return true;
    for(int i=1; i<=n; i++)
    {
        if(i>2 && s[i-2]=='X' &&s[i-1]=='X') return 0;
        if(i>1 && i<n && s[i-1]=='X' && s[i+1]=='X') return 0;
        if(i<n-1 && s[i+1]=='X' && s[i+2] == 'X') return 0;
    }
    int ans = 0, pre = 1;
    for( ; ; )
    {
        while(pre<=n && s[pre]=='X') pre++;
        if(pre>n) break;
        int k = pre;
        while(k<=n && s[k]=='.') k++;
        if(k<=n && pre>1 && s[pre-1]=='X'){
                if(s[k]=='X' && k-pre-4>0) ans ^= sg[k-pre-4];
        }
        else if(k-pre-2>0) ans ^= sg[k-pre-2];
        if(k>n) break;
        pre = k;
    }
    return ans==0;
}

void solve()
{
    scanf("%s", s+1);
    n = strlen(s+1);

    printf("Case %d:", cas++);
    int f = 1;
    for(int i=1; i<=n; i++)
    {
        if(!is_ok(i)) continue;
        s[i] = 'X';
        if(win(i))
            printf(" %d", i), f = 0;
        s[i] = '.';
    }
    if(f) printf(" 0");
    puts("");
}

int main()
{
//    freopen("in.txt", "r", stdin);
    init();
    cin>>_;
    while(_--) solve();
    return 0;
}

Problem E
HDU 4635（。。。。。。。。。。。。。。。。。，此处省略一万字）

Problem F
HDU 4711 。。

查看全文

相关阅读:
mac crontab
mac 修改MAC代码
 python 二叉树计算器
 python 验证码识别
 scp 上传和下载文件
 centos 开机执行的命令
 centos aws 修改使用密码ssh登录
 python nose测试
 C# linq to xml
Visual Studio 2015+InstallShield 2015

原文地址：https://www.cnblogs.com/zyx1314/p/3903558.html