这里只讲卷积在数组或者序列里的运算。卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列x(n)和h(n),则卷积的结果
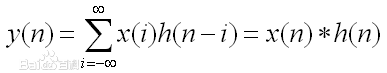
其中星号*表示卷积。当时序n=0时,序列h(-i)是h(i)的时序i取反的结果;时序取反使得h(i)以纵轴为中心翻转180度,所以这种相乘
后求和的计算法称为卷积和,简称卷积。另外,n是使h(-i)位移的量,不同的n对应不同的卷积结果。这是百度百科里的解释。
下面我们看一下知乎里面的简单实例解释:
不推荐用“反转/翻转/反褶/对称”等解释卷积。好好的信号为什么要翻转?导致学生难以理解卷积的物理意义。
这个其实非常简单的概念,国内的大多数教材却没有讲透。
直接看图,不信看不懂。以离散信号为例,连续信号同理。
已知
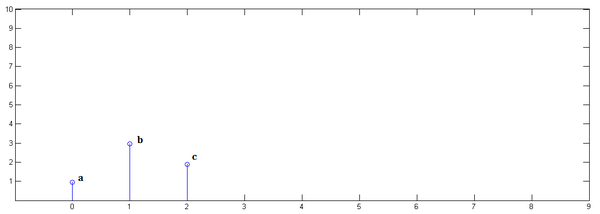
已知
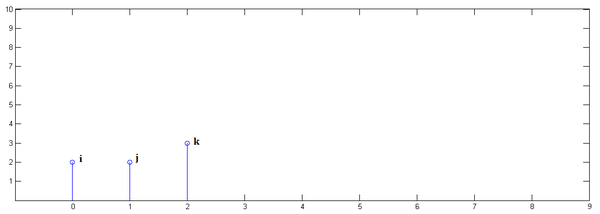
下面通过演示求的过程,揭示卷积的物理意义。
第一步,乘以
并平移到位置0:
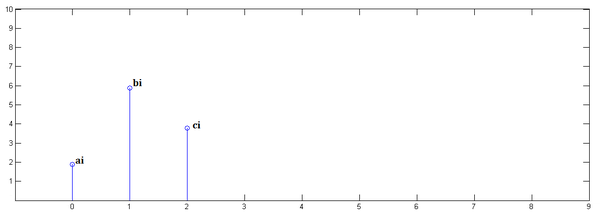
第二步,乘以
并平移到位置1:
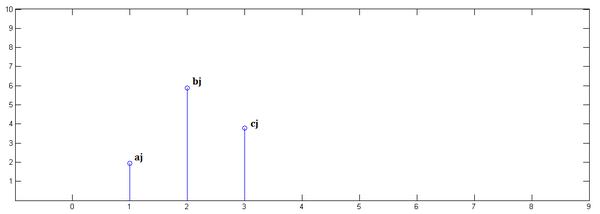
第三步,乘以
并平移到位置2:
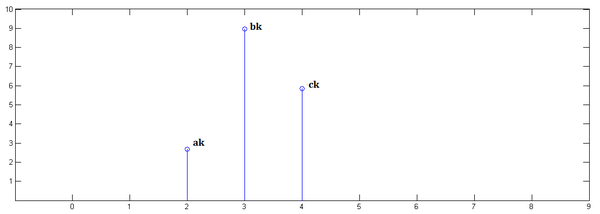
最后,把上面三个图叠加,就得到了:

简单吧?其实就是平移(没有反褶!)、叠加。
====================================================
在编程里通常对这个得到的新数组进行去头去尾的去值,选取中间完全迭代过的部分作为新的数组,以便下一个阶段的使用。通常得到的卷积后的新数组长度等于:用于卷积的两个数组长度的和减去一,而去头去尾,一般去掉新数组的头和尾各(较短数组长度减一)的值,留下中间完全迭代相加的数,由上图可以看出,卷积后的数组两头的数都是没有完全叠加的数,而中间部分的数则是完全叠加后得到的数值,这个一般用于赋权重来获取赋权后的值。比如:x=[1,2,3,4,5,6,7,8],y=[0.1,0.2,0.3,0.4],那么将x和y进行卷积运算后,得到的就是一个长度为len(x)+len(y)-1=11的数组,那么我们要用的肯定是中间全部赋过权重y的新的值,那么我们去掉头和尾部各3个值,剩下中间那5个值使我们能够使用的新的数组。
注意:这里一定要注意短数组的作用。
====================================================
从这里,可以看到卷积的重要的物理意义是:一个函数(如:单位响应)在另一个函数(如:输入信号)上的加权叠加。
重复一遍,这就是卷积的意义:加权叠加。
对于线性时不变系统,如果知道该系统的单位响应,那么将单位响应和输入信号求卷积,就相当于把输入信号的各个时间点的单位响应 加权叠加,就直接得到了输出信号。
通俗的说:
在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。
这正是单位响应是如此重要的原因。
在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。
这正是单位响应是如此重要的原因。
这正是单位响应是如此重要的原因。
作者:张俊博
链接:https://www.zhihu.com/question/22298352/answer/34267457
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。