科学计算与可视化-------------

一，读书笔记

Matplotlib

matplotlib是Python优秀的数据可视化第三方库
matplotlib库的效果可参考
http://matplotlib.org/gallery.html
matplotlib的使用 由各种可视化类构成，内部结构复杂，受matlab库启发，matplotlab.pyplot是绘制种类可视化图形的命令子库，相当于快捷方式
import matplotlib.pyplot as plt

绘制多图subplot

plot.subplot(nrows,ncols,plot_number)
在全局绘制区域中创建一个分区体系，并定位到一个子绘图区域

pyplot的plot()函数详解

plt.plot(x,y,format_string,**kwargs)
x:x轴数据，列表或数组，可选
y:y轴数据，列表或数组
format_string: 控制曲线的格式字符串，可迁
**kwargs: 第二组或更多的(x,y,format_string)

注意：当绘制多条曲线时，各条曲线的x不能省略

format_string：控制曲线的格式字符串，可选。由颜色字符、风格字符和标记字符组成

颜色字符	说明	颜色字符	说明
‘b‘	blue	‘m‘	magenta洋红色
‘g‘	green	‘y‘	黄色
‘r‘	red	‘k‘	黑色
‘c‘	cyan青绿色	‘w‘	白色
‘#008000‘	RGB某颜色	‘0.8‘	灰度值字符串

风格字符	说明
‘-‘	实线
‘--‘	破折线
‘-.‘	点划线
‘:‘	虚线
‘ ‘	无线条

标记字符	说明	标记字符	说明	标记字符	说明
‘.‘	点标记	‘1‘	下花三角标记	‘h‘	竖六边形标记
‘,‘	像素标记(极小点)	‘2‘	上花三角标记	‘H‘	横六边形标记
‘o‘	实心圏标记	‘3‘	左花三角标记	‘+‘	十字形标记
‘v‘	倒三角标记	‘4‘	右花三角标记	‘x‘	x标记
‘^‘	上三角标记	‘s‘	实心方形标记	‘D‘	菱形标记
‘>‘	右三角标记	‘p‘	实心五角标记	‘d‘	瘦菱形标记
‘<‘	左三角标记	‘*‘	星形标记	‘	‘

**kwargs: 第二组或更多(x,y,format_string)
color: 控制颜色 如color=‘green‘
linestyle:线条控制 如linestyle=‘dashed‘
marker:标记风格，marker=‘o‘
markerfacecolor:标记颜色，markerfacecolor=‘blue‘
markersize:标记尺寸，markersize=20
...

pyplot的中文显示

pyplot并不默认支持中文显示，需要rcParams修改字体实现

全局设置中文字体

import matplotlib
import matplotlib.pyplot as plt 
matplotlib.rcParams[‘font.family‘]=‘SimHei‘
plt.plot([3,1,4,5,2])
plt.ylabel(‘纵轴值‘)
plt.savefig(‘test‘,dpi=600)
plt.show()

rcParams的属性

属性	说明
‘font.family‘	用于显示字体的名字
‘font.style‘	字体风格，正常‘normal‘或斜体‘italic‘
‘font.size‘	字体大小，整数字号或者‘large‘,‘x-small‘

中文字体的种类

rcParams[‘font.family‘]
| 中文字体 | 说明 |
|------------|----------|
| ‘SimHei‘ | 中文黑体 |
| ‘Kaiti‘ | 中文楷体 |
| ‘LiSu‘ | 中文隶书 |
| ‘FangSong‘ | 中文仿宋 |
| ‘YouYuan‘ | 中文幼圆 |
| STSong | 华文宋体 |

局部设置中文字体

在有中文输出的地方，增加一个属性：fontproperties

pyplot的文本显示

pyplot的文本显示函数
| 函数 | 说明 |
|----------------|--------------------------|
| plt.xlabel() | 对x轴增加文本标签 |
| plt.ylabel() | 对y轴增加文本标签 |
| plt.title() | 对图形本整体增加文本标签 |
| plt.text() | 在任意位置增加文本 |
| plt.annotate() | 在图形中增加带箭头的注释 |

 Numpy

创建列表

a = [1, 2, 3, 4,5,6,7]

a[ : :-1]   # reversed a [7, 6, 5, 4, 3, 2, 1]

将列表转换为数组

b = np.array(a)  输出=>array([1, 2, 3, 4, 5])

 

数组基本操作 universal functions(ufunc)

b.sum()： #求和 10

b.min(),b.max(): #最小最大值

b[:6:2] = -10: # equivalent to a[0:6:2] = -10;   array([-10,2,-10,4,-10,6,-10])

from start to position 6, exclusive, set every 2nd element to -10

b.ravel(): # returns the array, flattened.拉伸成一行

b.T: # returns the array, transposed转置

a = np.floor(10*np.random.random((2,8))): #两行两列 随机 向下取整

array([[1., 2., 6., 3., 6., 7., 5., 2.],

              [2., 1., 9., 9., 1., 0., 0., 5.]])

np.hsplit(a,2): # Split a into 2 均分拆成2个数组 

[array([[1., 2., 6., 3.],[2., 1., 9., 9.]]), 

array([[6., 7., 5., 2.],[1., 0., 0., 5.]])]

np.hsplit(a,(3,4)): # Split a after the third and the fourth column 3 4 列开始切

np.hsplit(a,(3,5)): # Split a after the third and the fifth column 切成3份

np.hsplit(a,(3,4,5)): # Split a after the third ,forth, and fifth column 切成4份

np.abs(x)、np.fabs(x)： 计算数组各元素的绝对值

np.sqrt(x)： 计算数组各元素的平方根

np.square(x)： 计算数组各元素的平方

np.log(x),np.log10(x),np.log2(x)： 计算数组各元素的自然对数、10底对数和2底对数

np.ceil(x)： 计算数组各元素的ceiling值（向上）

np.floor(x)： 计算数组各元素的floor值（向下）

np.rint(x) ： 计算数组各元素的四舍五入值

np.add(b,c)： 数组b c相加

np.exp(b)： #b，c是数组 以自然常数e为底的指数函数，返回e的n次方，e 2.71828

np.modf(x) ： 将数组各元素的小数和整数部分以两个独立数组形式返回

c=np.array([2.5,1.3,-4.7])=>(array([ 0.5,  0.3, -0.7]), array([ 2.,  1., -4.]))

np.cos(x)、 np.cosh(x)、np.sin(x)、 np.sinh(x)、np.tan(x) 、np.tanh(x) ： 计算数组各元素的普通型和双曲型三角函数

np.sign(x) ： 计算数组各元素的符号值，1(正数), 0, -1(负数)

np.ones([10, 10])： 创建10行10列的数值为浮点1的矩阵

np.zeros([10, 10])： 创建10行10列的数值为浮点0的矩阵

 

Array Creation:

arange, array, copy, empty, empty_like, eye, fromfile, fromfunction, identity, 

linspace, logspace, mgrid, ogrid, ones, ones_like, r, zeros, zeros_like

Numpy查看数组属性

数组元素个数 b.size 输出=>5

数组形状 b.shape（行，列数）  输出=>(5,)

数组维度（维数） b.ndim  输出=>1

数组元素类型 b.dtype  输出=>dtype(‘int64‘)

itemsize： b.itemsize 输出=>8(type /8)

 

array(深拷贝Deep Copy)

d = a.copy()

asarray(浅拷贝Shallow Copy)

c = a.view()

 

Numpy创建随机数组np.random 均匀分布

np.random.rand(10, 10)创建指定形状(示例为10行10列)的数组(范围在0至1之间)

np.random.uniform(0, 100)创建指定范围内的一个数  50.502704296553915

np.random.randint(0, 100) 创建指定范围内的一个整数 25

 

正态分布 给定均值/标准差/维度的正态分布np.random.normal(1.75, 0.1, (2, 3))

    array([[1.69776327, 1.77925925, 1.64313181, 1.58202955, 1.75463511],

       [1.82200004, 1.6600281 , 1.71285888, 1.73226195, 1.88572285],

       [1.74169649, 1.7785425 , 1.6278489 , 1.67284158, 1.71138916],

       [1.69907805, 1.73646882, 1.71581448, 1.82025122, 2.0067373 ]])

 

改变数组形状(要求前后元素个数匹配),须得整除

  a1=np.ones([10]) 输出=>array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

  a2=a1.reshape([2,5])（变成2行5列）

   输出=>array([[1., 1., 1., 1., 1.],

       [1., 1., 1., 1., 1.]])

  a2=a1.reshape([3,])（变成3行，列未指定或为-1，由行计算出，此例不能被整除，报错）

Traceback (most recent call last):

  File "", line 1, in

ValueError: cannot reshape array of size 10 into shape (3,)

 

a1.resize([2，5]): a1直接变为2行5列

 

Manipulations:

array_split, column_stack, concatenate, diagonal, dsplit, dstack, hsplit, hstack, 

ndarray.item, newaxis, ravel, repeat, reshape, resize, squeeze, swapaxes, take, 

transpose, vsplit, vstack

 

条件运算

stus_score = np.array([[80, 88], [82, 81], [84, 75], [86, 83], [75, 81]])

stus_score > 80#符合为true，否则为false

np.where(stus_score < 80, 0, 90)#符合为0，否则90 三目运算符

 

统计运算

 指定轴最大值amax(参数1: 数组; 参数2: axis=0/1; 0表示列1表示行)：

  np.amax(stus_score, axis=0)  =>array([86, 88])

 指定轴最小值amin：

  np.amin(stus_score, axis=0)  =>array([75, 75])

 指定轴平均值mean：

  np.mean(stus_score, axis=1)  =>array([84. , 81.5, 79.5, 84.5, 78. ])

 方差std：

  np.std(stus_score, axis=0)  =>array([3.77359245, 4.1761226 ])

 

数组与数的运算

    # 为所有第一列都加5分

    stus_score[:, 0] = stus_score[:, 0]+5

    # 第一列减半

    stus_score[:, 0] = stus_score[:, 0]*0.5

 

数组间也支持加减乘除运算,但基本用不到

 a = np.array([1, 2, 3, 4])

 b = np.array([10, 20, 30, 40])

 c = a + b

 d = a - b

 e = a * b #elementwise product

 f = a / b

 b**2(b的每项平方)

 10*np.sin(a)

 b = np.linspace(0,pi,3)#从0到pi，均分，3个数

 

矩阵运算np.dot()

  (M行, N列) * (N行, Z列) = (M行, Z列)matrix product

q = np.array([[0.4], [0.6]])

result = np.dot(stus_score, q)

 

矩阵拼接Vector Stacking

x = np.arange(0,10,2)                     # x=([0,2,4,6,8])

y = np.arange(5)                          # y=([0,1,2,3,4])

  矩阵垂直拼接列数（列数须得相等，否则报错）

m = np.vstack([x,y])                      # m=([[0,2,4,6,8],

  #     [0,1,2,3,4]])

  矩阵水平拼接：（行数须得相等，否则报错）

xy = np.hstack([x,y])                     # xy =([0,2,4,6,8,0,1,2,3,4])

Numpy读取数据np.genfromtxt

csv文件以逗号分隔数据

构建csv文件，输入4行7列的内容，以逗号分隔

re=np.genfromtxt("a.csv",delimiter=",")

re

array([[ 1. ,  2. ,  3. ,  6. ,  4. ,  5. ,  6. ],

       [ 2. ,  6. ,  3. ,  6. ,  3. ,  6. ,  3. ],

       [ 3. , 66.3, 33.3, 33. ,  3.3,  6. ,  6.9],

       [ 4. ,  2. ,  3. ,  5. ,  3.3,  6.5,  9. ]])

如果数值据有无法识别的值出现,会以nan显示,nan相当于np.nan,为float类型（输入的是s）：

array([[ 1. ,  nan,  3. ,  6. ,  4. ,  5. ,  6. ],

       [ 2. ,  6. ,  3. ,  6. ,  3. ,  6. ,  3. ],

       [ 3. , 66.3, 33.3, 33. ,  3.3,  6. ,  6.9],

       [ 4. ,  2. ,  3. ,  5. ,  3.3,  6.5,  9. ]])

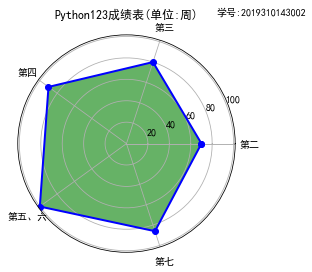
二，学习成绩雷达图：

代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed May  6 15:34:33 2020

@author: 49594
"""

#DrawDota.py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family']='SimHei'
matplotlib.rcParams['font.sans-serif']=['SimHei']
labels = np.array(['第二','第三','第四','第五、六','第七'])
nAttr = 5
data = np.array([70,80,90,100,86])#数据值
angles = np.linspace(0,2*np.pi,nAttr,endpoint=False)
data = np.concatenate((data,[data[0]]))#连接data和data[0]
angles = np.concatenate((angles,[angles[0]]))#连接angles和angles[0]
fig = plt.figure(facecolor="white")#创建一个全局绘图区域
plt.subplot(111,polar=True)
plt.title('Python123成绩表(单位:周)')
plt.plot(angles,data,'bo-',color='b',linewidth=2)
plt.fill(angles,data,facecolor='g',alpha=0.6)
plt.thetagrids(angles*180/np.pi,labels)#在各个angles的位置上标记上对应的labels
plt.figtext(0.72,0.95,'学号:2019310143002')#为全局绘图区添加文字
plt.grid(True)
plt.show()

三，手绘自定义：

原图如下：

代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed May  6 15:56:09 2020

@author: 49594
"""

#HandDrawpic.py
from PIL import Image
import numpy as np
vec_el = np.pi/2.2 #光源的俯视角度，弧度值
vec_az = np.pi/4. #光源的方位角度，弧度值
depth = 15.          #(0-100)
im = Image.open('66.jpg').convert('L')
a = np.asarray(im).astype('float')
grad = np.gradient(a)       #取图像灰度的梯度值
grad_x,grad_y = grad      #分别取横纵图像梯度值
grad_x = grad_x*depth/100.
grad_y = grad_y*depth/100.
dx = np.cos(vec_el)*np.cos(vec_az)   #光源对x轴的影响
dy = np.cos(vec_el)*np.sin(vec_az)   #光源对y轴的影响
dz = np.sin(vec_el)#光源对z轴的影响
A = np.sqrt(grad_x**2+grad_y**2+1.)
uni_x = grad_x/A
uni_y = grad_y/A
uni_z = 1./A
a2 = 255*(dx*uni_x+dy*uni_y+dz*uni_z)#光源归一化
a2 = a2.clip(0,255)
im2 = Image.fromarray(a2.astype('uint8'))#重构图像
im2.save('shouhui.jpg')

处理后，经过一定的测试比对，最终如下：

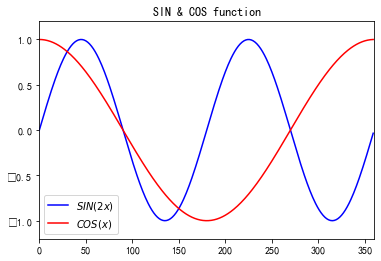
第四;绘制数学模型：sinx与cosx

代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed May  6 16:16:56 2020

@author: 49594
"""

#绘制基本的物理规律和函数
import numpy as np
import matplotlib.pyplot as pt
x = np.arange(0, 360)
print(x)
y = np.sin(2 * x * np.pi / 180.0)
z = np.cos(x * np.pi / 180.0)
# 使用美元符号把标签包围起来，得到 LaTex 公式显示的效果
pt.plot(x, y, color='blue', label="$SIN(2x)$")
pt.plot(x, z, color='red', label="$COS(x)$")
pt.xlim(0, 360)
pt.ylim(-1.2, 1.2)
pt.title("SIN & COS function")
# 要有 pt.legend() 这个方法才会显示图例
pt.legend()
pt.show()

图形如下：