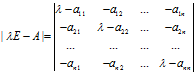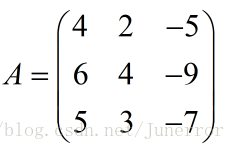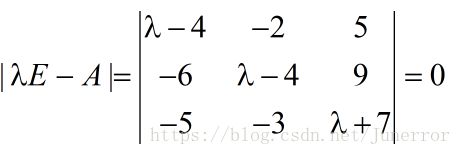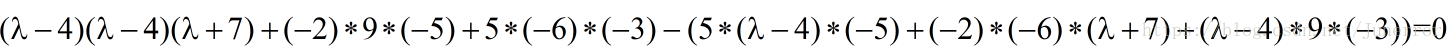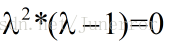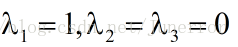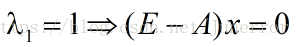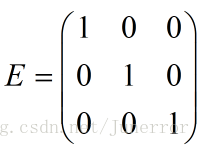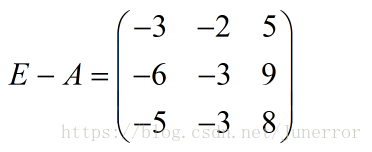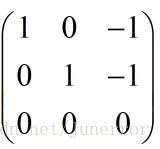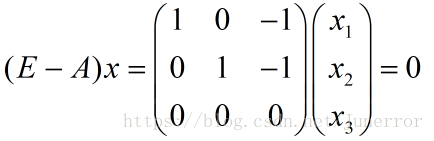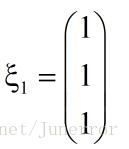一、先看一下教科书上的定义:设A是n阶方阵,如果存在常数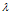 及非零n向量x,使得
及非零n向量x,使得 ,则称
,则称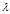 是矩阵A的特征值,x是A属于特征值
是矩阵A的特征值,x是A属于特征值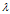 的特征向量。给定n阶矩阵A,行列式
的特征向量。给定n阶矩阵A,行列式
的结果是关于 的一个多项式,成为矩阵A的特征多项式,该特征多项式构成的方程
的一个多项式,成为矩阵A的特征多项式,该特征多项式构成的方程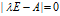 称为矩阵A的特征方程。
称为矩阵A的特征方程。
定理:n阶矩阵A的n个特征值就是其特征方程 的n个跟
的n个跟 ;而A的属于特征值
;而A的属于特征值 的特征向量就是其次线性方程
的特征向量就是其次线性方程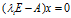 的非零解。
的非零解。
例:求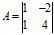 的特征根和特征向量
的特征根和特征向量
解: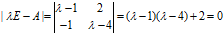 ,解一元二次方程可得
,解一元二次方程可得 ,
, ;
;
 对应的特征向量为x满足
对应的特征向量为x满足 ,求得
,求得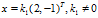
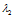 对应的特征向量为x满足
对应的特征向量为x满足 ,求得
,求得
二、例
计算:A的特征值和特征向量。
计算行列式得
化简得:
得到特征值:
化简得:
令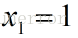
同理,当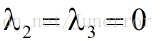
令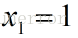
引自:
https://blog.csdn.net/Junerror/article/details/80222540
https://www.cnblogs.com/jiahuaking/p/3843071.html