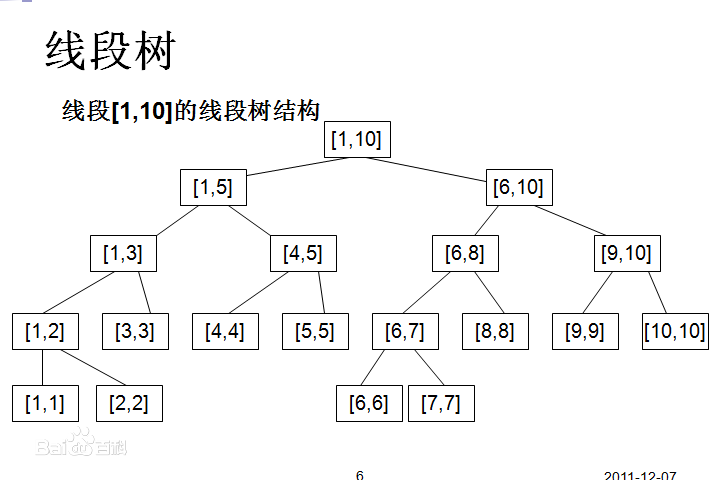
 (大概长这样)
(大概长这样)
注:本人未经过系统的学习线段树,可能理解有误,欢迎读者指出,但我相信按照我下面的解释,你一定能知道怎么写基本的线段树题,至少个人感觉读懂下文并不难。
定义:
void update(ll rn)// “ll”就是“long long”啦,题目需要,也忘了改了,请见谅qwq { sum[rn]=sum[rn<<1]+sum[rn<<1|1];//位运算符“<<1”相当于“*2”,“|1”相当于“+1”,“>>1”相当于“/2”; } void build(ll l,ll r,ll rn)//参数表示区间【l,r】和根节点rn { if(l==r) { sum[rn]=z[l];//我们不妨看一下图,当l=r时节点rn表示的是一个点l,所以直接赋上点值就好(至于数组名为什么叫z,忘了) return; } int m=(l+r)>>1; build(lson);//lson和rson的表示就是以上描述中提到的,下面完整代码中有它们的定义 build(rson); update(rn); //节点rn是lson和rson的父节点,恰好完全包含lson,rson表示的区间,所以sum[rn]应是两个儿子的“sum”之和,一直递归下去,树就建好了…… }
ll find(ll l,ll r,ll rn,ll nowl,ll nowr)//不要被参数名迷惑qwq,l,r,rn都是当前找到的节点的元素,你要询问的是nowl到nowr的什么什么东西(这里当然就是区间和了……) { ll ans=0; if(nowl<=l&&nowr>=r)//这句话说明当前区间已被你要找的区间完全包含,是它的一部分,那么我们就不用往下找了,理由见上面蓝色文字描述。 { return sum[rn];//找到一块小区间,返回 } int m=(l+r)>>1; if(nowl<=m)ans+=find(lson,nowl,nowr);//询问区间跨过了m说明在左儿子部分有一块区间 if(nowr>m)ans+=find(rson,nowl,nowr);//右端点跨过m+1说明在右儿子部分也有一块,那就递归下去逐块解决 return ans;//不要忘了返回累加答案(也许只有我会忘……) }
void _change(int l,int r,int rn,int p,int v) { //我们在【l,r】里面找到p使这个数加上v(变量名好随意的说)
if(l==r)//可以先看看下面的程序吧,当l=r时rn刚好锁定p,想一想为什么?
{
sum[rn]+=v;
return ;
}
int m=(l+r)>>1;
if(p<=m)_change(lson,p,v);//位置在左边就找左子树,不然找右子树,类似二分查找
if(p>m)_change(rson,p,v);
update(rn);//这就是来解决蓝字描述上的问题了
}
void put_col(ll rn,ll m,ll l,ll r)//参数为【l,r】,中点m,根节点rn(顺序好奇怪,瞎写的),参数可以只有l r rn,m可以算出来 { if(col[rn]) { col[rn<<1]+=col[rn]; col[rn<<1|1]+=col[rn];//这是将标记传递给下一代,因为可能更改多次再询问,所以标记是累加关系 sum[rn<<1]+=(m-l+1)*col[rn]; sum[rn<<1|1]+=(r-m)*col[rn];//显而易见的公式,每个元素都有一个相同的col,这个区间就会增大长度*col col[rn]=0;//注意清零,不然再查询就加多了…… } } void change(ll l,ll r,ll rn,ll v,ll nowl,ll nowr)//区间修改 { if(nowl<=l&&nowr>=r)//包含关系 { col[rn]+=v;//叠标记 sum[rn]+=v*(r-l+1); return; } int m=(l+r)>>1; put_col(rn,m,l,r);//向下传递标记 if(nowl<=m)change(lson,v,nowl,nowr); if(nowr>m)change(rson,v,nowl,nowr); update(rn);//这很重要,下面的值修改完了,递归到上一层 }
ll find(ll l,ll r,ll rn,ll nowl,ll nowr)
{
ll ans=0;
if(nowl<=l&&nowr>=r)
{
return sum[rn];
}
int m=(l+r)>>1;
put_col(rn,m,l,r);//为啥叫“懒”标记,因为它在修改时只是打上标记,欠了一屁股债,等到“find”再一并还清
if(nowl<=m)ans+=find(lson,nowl,nowr);
if(nowr>m)ans+=find(rson,nowl,nowr);
return ans;
}
#include<iostream>
#include<cstdio>
#define lson l,m,rn<<1
#define rson m+1,r,rn<<1|1
#define ll long long
using namespace std;
ll z[2000010],sum[4000010],n,M,question[2000010],total,col[2000010];
void update(ll rn)
{
sum[rn]=sum[rn<<1]+sum[rn<<1|1];
}
void build(ll l,ll r,ll rn)
{
if(l==r)
{
sum[rn]=z[l];
return;
}
int m=(l+r)>>1;
build(lson);
build(rson);
update(rn);
}
void put_col(ll rn,ll m,ll l,ll r)
{
if(col[rn])
{
col[rn<<1]+=col[rn];
col[rn<<1|1]+=col[rn];
sum[rn<<1]+=(m-l+1)*col[rn];
sum[rn<<1|1]+=(r-m)*col[rn];
col[rn]=0;
}
}
ll find(ll l,ll r,ll rn,ll nowl,ll nowr)
{
ll ans=0;
if(nowl<=l&&nowr>=r)
{
return sum[rn];
}
int m=(l+r)>>1;
put_col(rn,m,l,r);
if(nowl<=m)ans+=find(lson,nowl,nowr);
if(nowr>m)ans+=find(rson,nowl,nowr);
return ans;
}
void change(ll l,ll r,ll rn,ll v,ll nowl,ll nowr)
{
if(nowl<=l&&nowr>=r)
{
col[rn]+=v;
sum[rn]+=v*(r-l+1);
return;
}
int m=(l+r)>>1;
put_col(rn,m,l,r);
if(nowl<=m)change(lson,v,nowl,nowr);
if(nowr>m)change(rson,v,nowl,nowr);
update(rn);
}
void _change(int l,int r,int rn,int p,int v) {
if(l==r)
{
sum[rn]+=v;
return ;
}
int m=(l+r)>>1;
if(p<=m)_change(lson,p,v);
if(p>m)_change(rson,p,v);
update(rn);
}
int main()
{
scanf("%d%d",&n,&M);
for(int i=1;i<=n;i++)
cin>>z[i];
build(1,n,1);
for(int i=1;i<=M;i++)
{
ll x,y,z;
cin>>x;
if(x==1)
{
cin>>x>>y>>z;
change(1,n,1,z,x,y);
}else
{
cin>>y>>z;
question[++total]=find(1,n,1,y,z);
}
}
for(int i=1;i<=total;i++)printf("%lld\n",question[i]);
}//大家可以结合题意和上面的讲解自己理解一下,以下讲几个例题。
例题:
1.统计和(https://www.luogu.org/problemnew/show/P2068#sub)
这就是一道典型的单点修改和区间询问的裸题,没什么难度,直接放代码了:
#include<iostream>
#include<cstdio>
#define lson l,mid,rn<<1
#define rson mid+1,r,rn<<1|1
using namespace std;
int n,m,sum[100010],ans[100010],point;
void update(int rn)
{
sum[rn]=sum[rn<<1]+sum[rn<<1|1];
}
void change(int l,int r,int rn,int q,int v)
{
if(l==r)
{
sum[rn]+=v;
return;
}
int mid=(l+r)>>1;
if(q<=mid)change(lson,q,v);
if(q>mid)change(rson,q,v);
update(rn);
}
int find(int l,int r,int rn,int nowl,int nowr)
{
if(nowl<=l&&nowr>=r)
return sum[rn];
int ans=0;
int mid=(l+r)>>1;
if(nowl<=mid)ans+=find(lson,nowl,nowr);
if(nowr>mid)ans+=find(rson,nowl,nowr);
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
char a;
cin>>a;
if(a=='x')
{
int q,b;
scanf("%d%d",&q,&b);
change(1,n,1,q,b);
}
else
{
int x,y;
scanf("%d%d",&x,&y);
ans[++point]=find(1,n,1,x,y);
}
}
for(int i=1;i<=point;i++)
printf("%d\n",ans[i]);
}
2.在你窗外闪耀的星星(https://www.luogu.org/problemnew/show/P3353)//个人感觉题目描述还是挺不错的,说不定哪位兄弟有用呢(逃)
此题说白了就是区间和(不过这里我们来练习一下线段树的区间查询),我们枚举每个起点,如果窗户在这里,区间和是多少。然后取一个最大值,即为所求答案。
不过注意一下这个题目有一个坑点: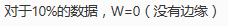 这个不合逻辑的东西是没法跑的(我试过……),所以特判输出0就好
这个不合逻辑的东西是没法跑的(我试过……),所以特判输出0就好
#include<iostream>
#include<cstdio>
#define lson l,mid,rn<<1
#define rson mid+1,r,rn<<1|1
using namespace std;
int n,m,ans1,sum[1000010],a[1000010];
void update(int rn)
{
sum[rn]=sum[rn<<1]+sum[rn<<1|1];
}
void change(int l,int r,int rn,int x,int y)
{
if(l==r)
{
sum[rn]+=y;
return;
}
int mid=(l+r)>>1;
if(x<=mid)change(lson,x,y);
if(x>mid)change(rson,x,y);
update(rn);
}
int find(int l,int r,int rn,int nowl,int nowr)
{
if(nowl<=l&&nowr>=r)
return sum[rn];
int mid=(l+r)>>1;
int ans=0;
if(nowl<=mid)ans+=find(lson,nowl,nowr);
if(nowr>mid)ans+=find(rson,nowl,nowr);
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
if(m==0)
{
printf("0");
return 0;
}
for(int i=1;i<=n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
change(1,n,1,x,y);
}
for(int i=1;i<=n;i++)
if(i+m-1<=n)
ans1=max(ans1,find(1,n,1,i,i+m-1));
else
break;
printf("%d",ans1);
}
3.I Hate It(https://www.luogu.org/problemnew/show/P1531)//这老师什么操作,校内黑幕?
这题考察单点修改和区间查询,不同的是,这次不是区间和,而是区间最值,其实就改两行就行了,题不难,请读者自行理解。
#include<iostream>
#include<cstdio>
#define lson l,mid,rn<<1
#define rson mid+1,r,rn<<1|1
using namespace std;
int n,m,sum[1000010],a[1000010],ans1[200010],point;
void update(int rn)
{
sum[rn]=max(sum[rn<<1],sum[rn<<1|1]);
}
void build(int l,int r,int rn)
{
if(l==r)
{
sum[rn]=a[l];
return;
}
int mid=(l+r)>>1;
build(lson);
build(rson);
update(rn);
}
void change(int l,int r,int rn,int x,int y)
{
if(l==r)
{
sum[rn]=max(y,sum[rn]);
return;
}
int mid=(l+r)>>1;
if(x<=mid)change(lson,x,y);
if(x>mid)change(rson,x,y);
update(rn);
}
int find(int l,int r,int rn,int nowl,int nowr)
{
if(nowl<=l&&nowr>=r)
return sum[rn];
int mid=(l+r)>>1;
int ans=0;
if(nowl<=mid)ans=max(find(lson,nowl,nowr),ans);
if(nowr>mid)ans=max(find(rson,nowl,nowr),ans);
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
build(1,n,1);
for(int i=1;i<=m;i++)
{
char now;
cin>>now;
if(now=='Q')
{
int x,y;
scanf("%d%d",&x,&y);
ans1[++point]=find(1,n,1,x,y);
}else
{
int x,y;
scanf("%d%d",&x,&y);
change(1,n,1,x,y);
}
}
for(int i=1;i<=point;i++)printf("%d\n",ans1[i]);
}
4.滑动窗口(https://www.luogu.org/problemnew/show/P1886)//貌似正解并不是线段树,但是我们还是拿来练一练吧。
比起上一道题我们只需要多存一个最小值就好,区间长度一定,只是起点在变,也是和上一题有许多相似点的
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<queue>
using namespace std;
#define lson l,mid,rn<<1
#define rson mid+1,r,rn<<1|1
int n,k,maxx[2000010],minn[2000010],a[2000010],ans1[2000010],ans2[2000010],point;
void update(int rn) {
maxx[rn]=max(maxx[rn<<1],maxx[rn<<1|1]);
minn[rn]=min(minn[rn<<1],minn[rn<<1|1]);
}
void build(int l,int r,int rn) {
if(l==r)
{
minn[rn]=maxx[rn]=a[l];
return;
}
int mid=(l+r)>>1; build(lson); build(rson); update(rn); } int find_max(int l,int r,int rn,int nowl,int nowr) {
if(nowl<=l&&nowr>=r)
return maxx[rn];
int mid=(l+r)>>1;
int ans=0;
if(nowl<=mid)ans=max(ans,find_max(lson,nowl,nowr));
if(nowr>mid)ans=max(ans,find_max(rson,nowl,nowr));
return ans;
}
int find_min(int l,int r,int rn,int nowl,int nowr) {
if(nowl<=l&&nowr>=r)
return minn[rn];
int mid=(l+r)>>1;
int ans=0x7fffffff;
if(nowl<=mid)ans=min(ans,find_min(lson,nowl,nowr));
if(nowr>mid)ans=min(ans,find_min(rson,nowl,nowr));
return ans;
}
int main() {
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
build(1,n,1);
for(int i=1;i<=n;i++)
{
int j=i+k-1;
if(j>n)break;
ans1[++point]=find_max(1,n,1,i,j);
ans2[point]=find_min(1,n,1,i,j);
}
for(int i=1;i<=point;i++)
printf("%d ",ans2[i]);
printf("\n");
for(int i=1;i<=point;i++)
printf("%d ",ans1[i]);
}
希望大家没有直接拿去交(还没交的同学可以找一下BUG)
好吧,我说了,对于每个区间,都需要查找两遍,max和min,所以一定会TLE,而且数组也开小了(为避免越界通常要开4n大小的数组)
那么能不能在找到max的同时找到min呢?
答案是肯定的,用全局变量记录就好了……
见代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<queue>
using namespace std;
#define lson l,mid,rn<<1
#define rson mid+1,r,rn<<1|1
int n,k,maxx[5000010],minn[5000010],a[5000010],ans1[5000010],ans2[5000010],point,find1;
void update(int rn)
{
maxx[rn]=max(maxx[rn<<1],maxx[rn<<1|1]);
minn[rn]=min(minn[rn<<1],minn[rn<<1|1]);
}
void build(int l,int r,int rn)
{
if(l==r)
{
minn[rn]=maxx[rn]=a[l];
return;
}
int mid=(l+r)>>1;
build(lson);
build(rson);
update(rn);
}
int find_max(int l,int r,int rn,int nowl,int nowr)
{
if(nowl<=l&&nowr>=r)
{
find1=min(find1,minn[rn]);
return maxx[rn];
}
int mid=(l+r)>>1;
int ans=-0x7fffffff;
if(nowl<=mid)ans=max(ans,find_max(lson,nowl,nowr));
if(nowr>mid)ans=max(ans,find_max(rson,nowl,nowr));
return ans;
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
build(1,n,1);
for(int i=1;i<=n;i++)
{
int j=i+k-1;
if(j>n)break;
find1=0x7fffffff;
ans1[++point]=find_max(1,n,1,i,j);
ans2[point]=find1;
}
for(int i=1;i<=point;i++)
printf("%d ",ans2[i]);
printf("\n");
for(int i=1;i<=point;i++)
printf("%d ",ans1[i]);
}
5.gcd区间(https://www.luogu.org/problemnew/show/P1890)
我们记录每个区间的gcd,完了。
#include<iostream>
#include<cstdio>
#include<algorithm>
#define lson l,mid,rn<<1
#define rson mid+1,r,rn<<1|1
using namespace std;
int n,m,a[1010],gcd[4013];
int _gcd(int a,int b)
{
if(b==0)return a;
return _gcd(b,a%b);
}
void update(int rn)
{
gcd[rn]=_gcd(gcd[rn<<1],gcd[rn<<1|1]);
}
void build(int l,int r,int rn)
{
if(l==r)
{
gcd[rn]=a[l];
return;
}
int mid=(l+r)>>1;
build(lson);
build(rson);
update(rn);
}
int find(int l,int r,int rn,int nowl,int nowr)
{
int ans=0;
if(nowl<=l&&nowr>=r)return gcd[rn];
int mid=(l+r)>>1;
if(nowl<=mid)ans=find(lson,nowl,nowr);
if(nowr>mid)ans=_gcd(ans,find(rson,nowl,nowr));
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
build(1,n,1);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
printf("%d\n",find(1,n,1,x,y));
}
}
相信通过上面的描述,大家应该都会写基本的线段树了,篇幅所限,例题不再列举,熟能生巧,大家多加练习吧!
完结,撒花。
注:本人致力于用通俗的语言来解析算法和数据结构,第一次写博客,多多包涵!