线性回归:预测归预测,误差肯定有

梯度下降:利用最小误差的平方求数据的最佳匹配函数

公式:公式结构
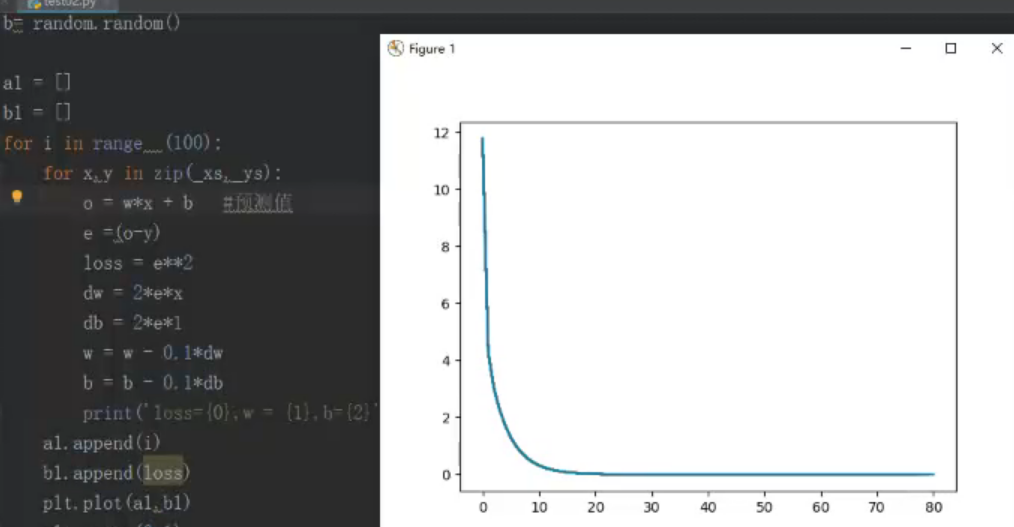
线性回归多数都是帮助人们生活中预测某一个东西比如天气的预测,身体内一些特有含量的预测,比如某某的值偏高,需要调节一下饮食,控制一下身体健康。
货运总量与工业总产值的数量关系进行研究,通过工业总产值预测货运总量。
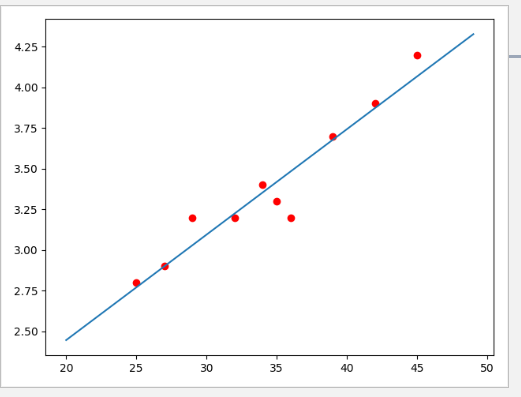
import matplotlib.pyplot as plt
import numpy as np
import random
y1 = [2.8,2.9,3.2,3.2,3.4,3.2,3.3,3.7,3.9,4.2] #运货量
x1 =[25,27,29,32,34,36,35,39,42,45] #工业值
xx_ = []
yy_=[]
xy_ = []
n=10
sum_y=0
sum_x=0
for x, y in zip(x1,y1):
x2 = x*x
y2 = y*y
xy = x*y
xx_.append(x2)
yy_.append(y2)
xy_.append(xy)
sum_y+=y
sum_x+=x
a1 = (n*sum(xy_)-(sum_x*sum_y))/(n*sum(xx_)-sum_x**2)
a0 = (sum_y/n)-a1*(sum_x/n)
print('a1 :',a1,'a0 :',a0)
x_ = np.arange(20,50)
y_ = a0 + a1 * x_
plt.subplots()
plt.scatter(x1,y1,c='red')
plt.plot(x_,y_)
plt.show()