Grids
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 953 Accepted Submission(s): 418
Problem Description
度度熊最近很喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。他想把1到2N这些数依次放进去,但是为了使格子看起来优美,他想找到使每行每列都递增的方案。不过画了很久,他发现方案数实在是太多了。度度熊想知道,有多少种放数字的方法能满足上面的条件?
Input
第一行为数据组数T(1<=T<=100000)。
然后T行,每行为一个数N(1<=N<=1000000)表示长方形的大小。
然后T行,每行为一个数N(1<=N<=1000000)表示长方形的大小。
Output
对于每组数据,输出符合题意的方案数。由于数字可能非常大,你只需要把最后的结果对1000000007取模即可。
Sample Input
2
1
3
Sample Output
Case #1:
1
Case #2:
5
Hint
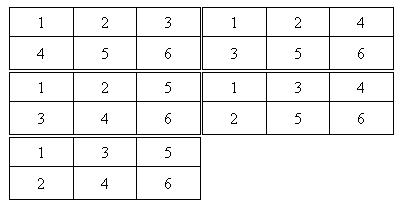
对于第二组样例,共5种方案,具体方案为:
Source
暴力找出前几项可知 1,2,5,14,42、、、容易看出是卡特兰数,递推公式 f(n+1)=(4*n-6)/n*f(n) | f(1)=f(2)=1 n>=2;
由于数很大需要取模用到了逆元,这里上界100w所以用了打表法,唯一要注意的一点就是,在处理4-6/n时,由于减法可能出现负数
我们写成 ( 4-6*inv[n]+mod )的形式但是这样还是会出现负数,因为6*inv[n]可能大于mod,这里只要多加几个mod即可解决
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define LL long long 4 const LL mod=1e9+7; 5 LL inv[1000005]={1,1}; 6 LL cat[1000005]={1,1,1}; 7 void init() 8 { 9 for(int i=2;i<=1000000;++i) 10 inv[i]=(mod-mod/i)*inv[mod%i]%mod; 11 for(int i=3;i<=1000001;++i) 12 cat[i]=cat[i-1]*((4+10*mod-6*inv[i-1])%mod)%mod; 13 } 14 int main() 15 { 16 int t,k=0,i,n; 17 scanf("%d",&t); 18 init(); 19 for(i=1;i<=t;++i){ 20 scanf("%d",&n); 21 printf("Case #%d: %lld ",i,cat[n+2]); 22 } 23 return 0; 24 }