初上概率论课程老师提及"布丰投针"实验,联想到这不就是上次做的那道概率吗,是在wcj同学的教导下用微积分求出来的,当时一脸懵逼,现在看到了一个更简单易懂的证明如下.

设针长为l<a,中点为M,M到离M最近的一条线的直线距离是x,针与这条线的夹角为α,则有0<=x<=a/2 , 0<=α<=PI , 当针与线相交时候显然有x<=sin(α)/2*l ,因此我们可以用图像来表示.
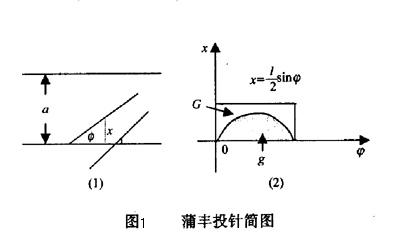
显然(2)图中的三角函数所占矩形的比率就是针与线相交的概率,反之则是不相交的概率。
P(交)={ ∫PI0 (l/2*sin(α)) d(α) } / (PI*a/2) = (2l) / (a*PI)