A.
链接:https://www.nowcoder.com/acm/contest/109/A
来源:牛客网
设三边长度为A,B,C,则有a=AB,b=BC,c=AC,枚举一下B如果满足B是a和b的因子且能满足c=AC,就直接计算输出结果。
来源:牛客网
题目描述
给出共享长方体一个顶点的三个面的面积,求它十二条边的边长和。
输入描述:
一行三个整数a, b, c表示面积(1 <= a, b, c <= 10000)。
输出描述:
一行一个整数表示边长和。
示例1
输入
1 1 1
输出
12
示例2
输入
4 6 6
输出
28
设三边长度为A,B,C,则有a=AB,b=BC,c=AC,枚举一下B如果满足B是a和b的因子且能满足c=AC,就直接计算输出结果。
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 using namespace std; 13 #define mp make_pair 14 #define pb push_back 15 #define debug puts("debug") 16 #define LL long long 17 #define pii pair<int,int> 18 #define eps 1e-10 19 int gcd(int a,int b){ 20 return b==0?a:gcd(b,a%b); 21 } 22 int main() 23 { 24 int n,m,i,j,k; 25 LL a,b,c; 26 LL A,B,C; 27 cin>>a>>b>>c; 28 n=max(a,b); 29 for(B=1;B<=n;++B){ 30 if(a%B==0&&b%B==0){ 31 if(c==a/B*b/B){ 32 cout<<4*(B+a/B+b/B)<<endl; 33 return 0; 34 } 35 } 36 } 37 return 0; 38 }
B.
链接:https://www.nowcoder.com/acm/contest/109/B
来源:牛客网
kmp跑一波遇见怎么也无法匹配的点就输出no即可。
来源:牛客网
题目描述
给出两个串s和x
定义s中的某一位i为好的位置,当且仅当存在s的子序列) 满足y=x且存在j使得i=kj成立。
满足y=x且存在j使得i=kj成立。
问s中是否所有的位置都是好的位置。
定义s中的某一位i为好的位置,当且仅当存在s的子序列
问s中是否所有的位置都是好的位置。
输入描述:
一行两个字符串s,x,这两个串均由小写字母构成。
1 <= |s|, |x| <= 200000
输出描述:
Yes表示是。
No表示不是。
示例1
输入
abab ab
输出
Yes
示例2
输入
abacaba aba
输出
No
示例3
输入
abc ba
输出
No
kmp跑一波遇见怎么也无法匹配的点就输出no即可。
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 using namespace std; 13 #define mp make_pair 14 #define pb push_back 15 #define debug puts("debug") 16 #define LL long long 17 #define pii pair<int,int> 18 #define eps 1e-10 19 LL R=6371009; 20 int f[202020]; 21 int g[202020]; 22 char s[202020]; 23 char x[202020]; 24 int main() 25 { 26 int n,m,i,j,k; 27 double x1,y1,x2,y2; 28 scanf("%s%s",s,x); 29 int n1=strlen(s); 30 int n2=strlen(x); 31 f[0]=-1; 32 for(i=1;i<=n2;++i){ 33 j=f[i-1]; 34 while(j!=-1&&x[i-1]!=x[j]) j=f[j]; 35 f[i]=j+1; 36 } 37 for(i=0,j=0;i<n1;++i){ 38 if(s[i]==x[j]){ 39 j++; 40 } 41 else{ 42 while(j!=-1&&x[j]!=s[i]) j=f[j]; 43 j++; 44 } 45 if(j==n2){ 46 g[i]=n2; 47 j=f[j]; 48 // j++; 49 } 50 } 51 int l=n1; 52 bool ok=1; 53 // for(i=0;i<n1;++i) 54 // cout<<"gi="<<g[i]<<endl; 55 for(i=n1-1;i>=0;--i){ 56 if(g[i]==0&&l>=i){ 57 ok=0; 58 break; 59 } 60 if(g[i]){ 61 l=i-n2; 62 } 63 } 64 ok?puts("Yes"):puts("No"); 65 return 0; 66 } 67 68 /* 69 ababbab 70 ab 71 */
C.
链接:https://www.nowcoder.com/acm/contest/109/C
来源:牛客网
题目描述
给定长度为n的数组a,定义一次操作为:
1. 算出长度为n的数组s,使得si= (a[1] + a[2] + ... + a[i]) mod 1,000,000,007;
2. 执行a = s;
现在问k次操作以后a长什么样。
1. 算出长度为n的数组s,使得si= (a[1] + a[2] + ... + a[i]) mod 1,000,000,007;
2. 执行a = s;
现在问k次操作以后a长什么样。
输入描述:
第一行两个整数n,k(1 <= n <= 2000, 0 <= k <= 1,000,000,000);i
第二行n个整数表示a数组(0 <= a
<= 1,000,000,000)。
输出描述:
一行n个整数表示答案。
示例1
输入
3 1 1 2 3
输出
1 3 6
示例2
输入
5 0 3 14 15 92 6
输出
3 14 15 92 6
首先注意到这个操作可以用矩阵来表示,设原数组为一个行向量A,k次操作之后得到的行向量B, 转移矩阵为X,则有A*Xk=B ,观察发现X是一个N*N的上三角矩阵,
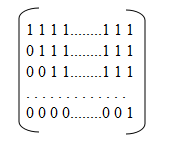
可即使使用了快速幂,这个矩阵一次乘法的时间复杂度也不允许接受,因为N<=2000,N^3过于庞大,枚举了这个矩阵的前几次方之后发现一个规律,这个矩阵只要知道
第一行的元素就可以推出这个全部的矩阵,每一列都来自于第一行的一个子段,再观察发现这些数字都是杨辉三角里的数,准确的说这一行数对应杨辉三角的一列(斜着),
对于X^k,这个矩阵,第一行的元素就是( C(k-1,0) , C(k,1) , C(k+1,2),.....C(k+n-2,n-1)),组合数的公式C(n,r)=C(n,r-1)*(n-r+1)/r,
C(n,r)=C(n-1,r)+C(n-1,r-1),联立得出C(n,r)=C(n-1,r-1)*n/r,有除法记得取逆元。
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 using namespace std; 13 #define mp make_pair 14 #define pb push_back 15 #define debug puts("debug") 16 #define LL long long 17 #define pii pair<int,int> 18 #define eps 1e-10 19 double R=6371009; 20 21 LL MOD=1e9+7; 22 LL q[2020]; 23 LL a[2020]; 24 void gcd(LL a,LL b,LL &d,LL &x,LL &y) 25 { 26 if(!b) {d=a;x=1;y=0;} 27 else {gcd(b,a%b,d,y,x);y-=x*(a/b);} 28 } 29 LL inv(LL a,LL n) 30 { 31 LL d,x,y; 32 gcd(a,n,d,x,y); 33 return d==1?(x+n)%n:-1; 34 } 35 int main() 36 { 37 LL n,m,i,j,k; 38 scanf("%lld%lld",&n,&k); 39 for(i=1;i<=n;++i) scanf("%lld",a+i); 40 k--; 41 q[1]=1; 42 for(i=2;i<=n;++i){ 43 q[i]=q[i-1]*((k+i-1)%MOD)%MOD*inv(i-1,MOD); 44 q[i]%=MOD; 45 } 46 //for(i=2;i<=n;++i) q[i]+=q[i-1],q[i]%=MOD; 47 for(i=1;i<=n;++i){ 48 LL tmp=0; 49 for(j=1;j<=i;++j){ 50 tmp+=a[j]*q[i-j+1]; 51 tmp%=MOD; 52 } 53 printf("%lld%c",tmp,i==n?' ':' '); 54 } 55 return 0; 56 }
E.
链接:https://www.nowcoder.com/acm/contest/109/E
来源:牛客网
题目描述
给定一幅n个点m条边的图和S个一定要经过的点,问从0号点出发,经过这S个点再回到0号点的最短路径长度是多少。
输入描述:
第一行一个整数T(T <= 2)表示数据组数。
对于每组数据,第一行两个整数n,m表示点数和边数(1 <= n, m <= 100,000)。
接下来m行,每行三个整数x, y, z(0 < x, y < n, 0 <= z <= 1000)表示xy之间有一条长度为c的双向边;
接下来一个整数S。(S<=10)
接下来S行每行一个整数表示一定要经过的点。
数据保证有解。
输出描述:
T行,每行一个整数表示答案。
示例1
输入
1 4 6 0 1 1 1 2 1 2 3 1 3 0 1 0 2 5 1 3 5 3 1 2 3
输出
4
全卡在C没来得及看这个其实不难,跑S+1(0和必经的S个点)次最短路,将点离散化然后dp,f[S][i]表示当前走的点的集合S且最后一个经过的点为i点的最短路径,
最后枚举全集加上dis(0,i)即可。优先队列忘记重载比较算子神特么过了样例结果一直WA,还有前向星蜜汁写错,可能老了= =
1 #include<iostream> 2 #include<cstring> 3 #include<queue> 4 #include<cstdio> 5 #include<stack> 6 #include<set> 7 #include<map> 8 #include<cmath> 9 #include<ctime> 10 #include<time.h> 11 #include<algorithm> 12 using namespace std; 13 #define mp make_pair 14 #define pb push_back 15 #define debug puts("debug") 16 #define LL long long 17 #define pii pair<int,int> 18 #define eps 1e-10 19 #define inf 0x3f3f3f3f 20 struct Edge{ 21 int v,w,next; 22 }e[202020]; 23 int first[101010],tot; 24 void add(int u,int v,int w){ 25 e[tot].v=v; 26 e[tot].w=w; 27 e[tot].next=first[u]; 28 first[u]=tot++; 29 } 30 int f[(1<<12)][12]; 31 int d[12][101010]; 32 bool vis[101010]; 33 int x[15]; 34 int N,M,S; 35 void dij(int s,int ps){ 36 memset(vis,0,sizeof(vis)); 37 d[ps][s]=0; 38 priority_queue<pii,vector<pii>,greater<pii> >q; 39 q.push(mp(0,s)); 40 while(!q.empty()){ 41 int u=q.top().second; 42 q.pop(); 43 if(vis[u]) continue; 44 vis[u]=1; 45 for(int i=first[u];i!=-1;i=e[i].next){ 46 int v=e[i].v,w=e[i].w; 47 if(d[ps][v]>d[ps][u]+w){ 48 d[ps][v]=d[ps][u]+w; 49 q.push(mp(d[ps][v],v)); 50 } 51 } 52 } 53 } 54 55 int main() 56 { 57 int t,i,j,k; 58 scanf("%d",&t); 59 while(t--){ 60 memset(d,inf,sizeof(d)); 61 memset(first,-1,sizeof(first)); 62 tot=0; 63 int u,v,w; 64 scanf("%d%d",&N,&M); 65 while(M--){ 66 scanf("%d%d%d",&u,&v,&w); 67 add(u,v,w); 68 add(v,u,w); 69 } 70 71 72 scanf("%d",&S); 73 dij(0,0); 74 x[0]=0; 75 for(i=1;i<=S;++i){ 76 scanf("%d",&u); 77 x[i]=u; 78 dij(u,i); 79 } 80 memset(f,inf,sizeof(f)); 81 f[1][0]=0; 82 for(int s=0;s<=(1<<(S+1));s++){ 83 for(j=0;j<=S;++j){ 84 if(f[s][j]!=inf){ 85 for(int k=0;k<=S;++k){ 86 if((s&(1<<k))==0&&d[j][x[k]]!=inf){ 87 f[s|(1<<k)][k]=min(f[s|(1<<k)][k],f[s][j]+d[j][x[k]]); 88 } 89 } 90 } 91 } 92 } 93 94 int ans=inf; 95 int all=(1<<(S+1))-1; 96 for(i=0;i<=S;++i) 97 ans=min(ans,f[all][i]+d[0][x[i]]); 98 cout<<ans<<endl; 99 } 100 return 0; 101 }