hdu-5492-dp

Find a path

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2068    Accepted Submission(s): 893

Problem Description

Frog fell into a maze. This maze is a rectangle containing N rows and M columns. Each grid in this maze contains a number, which is called the magic value. Frog now stays at grid (1, 1), and he wants to go to grid (N, M). For each step, he can go to either the grid right to his current location or the grid below his location. Formally, he can move from grid (x, y) to (x + 1, y) or (x, y +1), if the grid he wants to go exists.
Frog is a perfectionist, so he'd like to find the most beautiful path. He defines the beauty of a path in the following way. Let’s denote the magic values along a path from (1, 1) to (n, m) as A1,A2,…AN+M−1, and Aavg is the average value of all Ai. The beauty of the path is (N+M–1) multiplies the variance of the values:(N+M−1)∑N+M−1i=1(Ai−Aavg)2
In Frog's opinion, the smaller, the better. A path with smaller beauty value is more beautiful. He asks you to help him find the most beautiful path. 

 

Input

The first line of input contains a number T indicating the number of test cases (T≤50).
Each test case starts with a line containing two integers N and M (1≤N,M≤30). Each of the next N lines contains M non-negative integers, indicating the magic values. The magic values are no greater than 30.

 

Output

For each test case, output a single line consisting of “Case #X: Y”. X is the test case number starting from 1. Y is the minimum beauty value.

 

Sample Input

1 2 2 1 2 3 4

 

Sample Output

Case #1: 14

 

Source

2015 ACM/ICPC Asia Regional Hefei Online

 

 

  求方格迷宫里的最小方差路径。

  化简式子:    

  

  

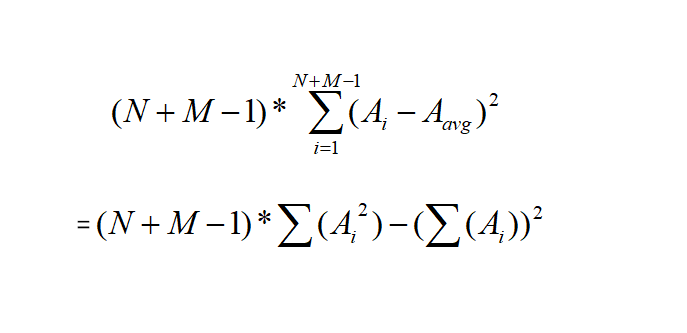
    可以看出问题就是要使得所有的（N+M-1）*（A平方的和）减去所有A的和的平方达到最小。

   令f[i][j][k]表示走到(i,j)处，且当前走过的格子的法力值的和为k（即SUM{A}=k）的时候的最小的SUM{Ai^2}的值。

   最后答案就是MIN{ f[i][j][k]*(N+M-1)-k*k }

  

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
int f[35][35][2000]; 
int e[35][35];
int main(){
    int N,M,T,i,j,k;
    cin>>T;
    for(int cas=1;cas<=T;++cas){
        cin>>N>>M;
        for(i=1;i<=N;++i){
            for(j=1;j<=M;++j){
                cin>>e[i][j];
            }
        }
    memset(f,inf,sizeof(f));
    f[1][1][e[1][1]]=e[1][1]*e[1][1];
    for(i=1;i<=N;++i){
        for(j=1;j<=M;++j){
            for(k=0;k<2000;++k){
                if(f[i][j][k]!=inf){
                    f[i][j+1][k+e[i][j+1]]=min(f[i][j+1][k+e[i][j+1]],f[i][j][k]+e[i][j+1]*e[i][j+1]);
                    f[i+1][j][k+e[i+1][j]]=min(f[i+1][j][k+e[i+1][j]],f[i][j][k]+e[i+1][j]*e[i+1][j]);
                }
            }
        }
    }
    int ans=inf;
    for(i=0;i<2000;++i){
        if(f[N][M][i]!=inf){
            ans=min(ans,f[N][M][i]*(N+M-1)-i*i);
        }
    }
    cout<<"Case #"<<cas<<": "<<ans<<endl;    
    }
    return 0;
}