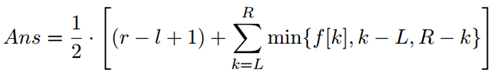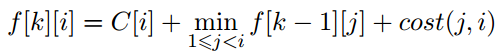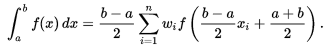life
这个出题人怎么这么暴力啊
我们把所有长度为l-1的串搞出来,每个长度为l的串前缀往后缀连边。
那么我们只要找到一条欧拉回路就行了。
但是这题tmd卡空间。。。暴力建边过不了,似乎要用哈希值动态建图。。。就当过了好了
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define S 1000000 int M=0,fst[S],vb[S+S],vc[S+S],nxt[S+S]; void ad_de(int a,int b,int c) { ++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; vc[M]=c; } int c,l; char s[S+S]; void dfs(int d=0,int ch=0,int tat=0,int lst=0,int lch=0) { if(d==l) { ad_de(ch,lst,lch); return; } for(int x=0;x<c;x++) { dfs(d+1,(d)?(ch*c+x):ch,tat*c+x,tat,x); } } int st[S+S],ss=0; void euler(int c) { for(int i=fst[c];i;) { fst[c]=nxt[i]; st[++ss]=vc[i]; euler(vb[i]); i=fst[c]; } fst[c]=0; } int main() { freopen("life.in","r",stdin); freopen("life.out","w",stdout); scanf("%d%d%s",&c,&l,s); if(l==1) { puts(s); return 0; } dfs(0); euler(0); printf("%d ",ss+l-1); for(int i=1;i<l;i++) putchar(s[0]); for(int i=ss;i>=1;i--) putchar(s[st[i]]); }
gene
1<=n,m<=130000,s由ACTG组成。
首先我们把字符串,例如abcd变成|a|b|c|d|,然后跑manacher,搞出p数组(向左向右最长对称长度,从0开始)。
经过观察我们可以知道,如果x位置这个字符是分隔符,那么实际以它为中心存在回文串个数为p[k]/2,否则存在(p[k]+1)/2个。
那我们对于一个询问[l,r],考虑在这个新串里面就是[2l-1,2r+1],(实际写出来好像由于从0开始标号不是这样...详见代码)那么设L=2l-1,R=2r+1。
我们可以发现:
r-l+1是为了补偿x不为分隔符时的那个1。
接下来我们来暴力讨论一波那个min。
如果k-L<=R-k时,即L<=k<=l+r。
此时答案就成了min{f[k],k-L},那么如果f[k]<=k-L,即f[k]-k<=-L,就将f[k]计入答案。如果f[k]-k>L,就将k-L计入答案。
如果k-L>R-k,l+r<k<=R。
答案成了min{f[k],R-k},如果f[k]<=R-k,即f[k]+k<=R,就将f[k]计入答案,否则将R-k计入答案。
两棵可持久化线段树(维度为x,f[x]-x和x,f[x]+x)解决问题...
出题人强行卡常...卡不过去
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define SZ 666666 #define inf 1000000001 int A; struct tup { ll s[3]; tup() {s[0]=s[1]=s[2]=0;} tup(ll a,ll b,ll c) {s[0]=a; s[1]=b; s[2]=c;} ll& operator [] (int a) {return s[a];} }; bool operator < (tup a,tup b) {return 0;} tup operator + (tup a,tup b) {return tup(a[0]+b[0],a[1]+b[1],a[2]+b[2]);} tup operator - (tup a,tup b) {return tup(a[0]-b[0],a[1]-b[1],a[2]-b[2]);} typedef pair<pii,tup> rec; bool cmp(rec a,rec b) {return a.fi.fi<b.fi.fi;} struct Query2D { #define S2 7000000 int ch[S2][2],rots[SZ],an,pn; tup sum[S2]; rec ps[SZ]; Query2D() {an=pn=0;} int P_,S_; tup Q_; void ins_(int r1,int& r2,int l,int r) { r2=++an; sum[r2]=sum[r1]+Q_; if(l==r) return; int mid=l+r>>1; if(P_<=mid) ins_(ch[r1][0],ch[r2][0],l,mid), ch[r2][1]=ch[r1][1]; else ins_(ch[r1][1],ch[r2][1],mid+1,r), ch[r2][0]=ch[r1][0]; } ll query_(int r1,int r2,int l,int r) { if(l>P_||sum[r1][S_]==sum[r2][S_]) return 0; if(r<=P_) return sum[r2][S_]-sum[r1][S_]; int mid=l+r>>1; ll ans=query_(ch[r1][0],ch[r2][0],l,mid); if(P_>mid) ans+=query_(ch[r1][1],ch[r2][1],mid+1,r); return ans; } void ins(int x,int y,tup z) { ++x; y+=A; ++pn; ps[pn].fi.fi=x; ps[pn].fi.se=y; ps[pn].se=z; //if(pn&131071);else cerr<<pn<<"mdzz "; } int fst[SZ],nxt[SZ]; void pre() { for(int i=1;i<=pn;i++) { int x=ps[i].fi.fi; nxt[i]=fst[x]; fst[x]=i; } int cur=1,rr=0,rt=0; for(int i=1;i<=A+A;i++) { for(int cur=fst[i];cur;cur=nxt[cur]) { P_=ps[cur].fi.se; Q_=ps[cur].se; ins_(rr,rt,0,A+A+A); rr=rt; } rots[i]=rt; } //cerr<<an<<"yikesaiting "; } ll query(int x1,int x2,int y1,int y2,int s) { if(x1>x2||y1>y2) return 0; ++x1; ++x2; y1+=A; y2+=A; P_=y2; S_=s; ll ans=query_(rots[x1-1],rots[x2],0,A+A+A); P_=y1-1; ans-=query_(rots[x1-1],rots[x2],0,A+A+A); return ans; } }k_fk_m_k,k_fk_a_k; int n,m,p[SZ]; char dna[SZ],s[SZ]; void manacher() { int ml=0,id=0; for(int i=1;s[i];i++) { if(ml>i) p[i]=min(p[2*id-i],p[id]+id-i); else p[i]=1; while(i-p[i]>=0&&s[i+p[i]]==s[i-p[i]]) p[i]++; if(i+p[i]>ml) ml=i+p[i], id=i; } for(int i=1;s[i];i++) --p[i]; } #define gc getchar() int g_i() { int tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return -tmp; else return tmp; } #define gi g_i() #define pob #define pc(x) putchar(x) namespace ib {char b[100];} inline void pint(int x) { if(x==0) {pc(48); return;} if(x<0) {pc('-'); x=-x;} char *s=ib::b; while(x) *(++s)=x%10, x/=10; while(s!=ib::b) pc((*(s--))+48); } int main() { freopen("gene.in","r",stdin); freopen("gene.out","w",stdout); scanf("%d%d%s",&n,&m,dna); int ps=0; s[ps++]='*'; for(int i=0;dna[i];i++) { s[ps++]=dna[i]; s[ps++]='*'; } s[ps]=0; manacher(); A=ps+3; for(int i=0;s[i];i++) { k_fk_m_k.ins(i,p[i]-i,tup(p[i],i,1)); k_fk_a_k.ins(i,p[i]+i,tup(p[i],i,1)); } k_fk_m_k.pre(); k_fk_a_k.pre(); while(m--) { int l=gi,r=gi,L=l+l-2,R=r+r; --l; --r; ll ans=r-l+1; ans+=k_fk_m_k.query(L,l+r,-A,-L,0); ans+=k_fk_m_k.query(L,l+r,-L+1,A+A,1) -k_fk_m_k.query(L,l+r,-L+1,A+A,2)*L; ans+=k_fk_a_k.query(l+r+1,R,-A,R,0); ans+=k_fk_a_k.query(l+r+1,R,R+1,A+A,2)*R -k_fk_a_k.query(l+r+1,R,R+1,A+A,1); ans/=2; printf("%I64d ",ans); } }
jhaha(暴力的题目名称
n<=20000,m<=100。
我们考虑一个思博暴力,令f[k][i]为前k个建了i个记者站,最后一个记者站为k的最小花费(包括i之前的没覆盖的费用)。
方程大概这样...
我们考虑从小到大枚举i。
首先我们可以随便sort一下拿个指针弄一下,搞出前i个,第i个造了记者站,没覆盖的费用。后i个同理。
那么首先我们可以这样求出f[?][1]这一堆。
然后我们考虑已知f[?][x-1],如何求出f[?][x],我们从小到大枚举第一维s,如果我们考虑从p转移,那么就要从f[p][x-1]+cost(p...s)转移。
现在s变大的时候我们可以发现和之前指针搞的一样,渐渐地会有一些村庄w不能被s覆盖,那么p如果不能覆盖w,答案就要加上P[w]。
我们可以二分出哪里结束不能覆盖,然后拿棵线段树维护一下就行了。
好消息,我又被卡常了...
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first #define SZ 666666 int bits[SZ]; int n,m; int d[SZ],c[SZ],r[SZ],p[SZ]; int M=32768,M2=M+M,ls[SZ],rs[SZ]; int qq[SZ],tag[SZ]; void build() { for(int i=M+1;i<=M+M;i++) ls[i]=rs[i]=i-M; for(int i=M-1;i;i--) { ls[i]=ls[i+i], rs[i]=rs[i+i+1], qq[i]=min(qq[i+i],qq[i+i+1]); } } void pd(int x) { if(tag[x]) { qq[x]+=tag[x]; if(x+x<=M2) tag[x+x]+=tag[x], tag[x+x+1]+=tag[x]; tag[x]=0; } } void upd(int x) { pd(x+x); pd(x+x+1); qq[x]=min(qq[x+x],qq[x+x+1]); } void edit(int x,int ql,int qr,int v) { if(x>M2||ql>qr) return; pd(x); if(ql==ls[x]&&qr==rs[x]) {tag[x]+=v; return;} int mid=ls[x]+rs[x]>>1; edit(x+x,ql,min(qr,mid),v); edit(x+x+1,max(mid+1,ql),qr,v); upd(x); } int gmin(int x,int ql,int qr) { if(x>M2||ql>qr) return 1000000000; pd(x); if(ql==ls[x]&&qr==rs[x]) return qq[x]; int mid=ls[x]+rs[x]>>1; int ans=min(gmin(x+x,ql,min(qr,mid)),gmin(x+x+1,max(mid+1,ql),qr)); upd(x); return ans; } int gmin(int x) { return gmin(1,1,x); } void edt(int x,int y) { edit(1,1,x,y); } void init(int n,int* x) { memset(qq,127/3,sizeof(qq)); memset(tag,0,sizeof(tag)); for(int i=n;i>=1;i--) qq[i+M]=x[i]; build(); } int lf[SZ],qzc[SZ],hzc[SZ]; pii t[SZ]; int f[101][20001]; #define gc getchar() int g_i() { int tmp=0; bool fu=0; char s; while(s=gc,s!='-'&&(s<'0'||s>'9')) ; if(s=='-') fu=1; else tmp=s-'0'; while(s=gc,s>='0'&&s<='9') tmp=tmp*10+s-'0'; if(fu) return -tmp; else return tmp; } #define gi g_i() int main() { freopen("jhaha.in","r",stdin); freopen("jhaha.out","w",stdout); n=gi, m=gi; for(int i=2;i<=n;i++) d[i]=gi; for(int i=1;i<=n;i++) c[i]=gi; for(int i=1;i<=n;i++) r[i]=gi; for(int i=1;i<=n;i++) p[i]=gi; for(int i=1;i<=n;i++) lf[i]=lower_bound(d+1,d+1+n,d[i]-r[i])-d; for(int i=1;i<=n;i++) t[i]=pii(d[i]-r[i],i); sort(t+1,t+1+n); for(int i=n,j=n;i>=1;i--) { hzc[i]=hzc[i+1]; while(j>=1&&t[j].first>d[i]) hzc[i]+=p[t[j--].second]; } for(int i=1;i<=n;i++) t[i]=pii(d[i]+r[i],i); sort(t+1,t+1+n); for(int i=1,j=1;i<=n;i++) { qzc[i]=qzc[i-1]; while(j<=n&&t[j].first<d[i]) qzc[i]+=p[t[j++].second]; } for(int i=1;i<=n;i++) f[1][i]=qzc[i]+c[i]; for(int i=2;i<=m;i++) { init(n,f[i-1]); //要把数组倒过来 for(int j=1,k=1;j<=n;j++) { while(k<=n&&t[k].first<d[j]) edt(lf[t[k].second]-1,p[t[k].second]), ++k; f[i][j]=gmin(j-1)+c[j]; } } int ans=2147483647; for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) ans=min(ans,f[i][j]+hzc[j]); } printf("%d ",ans); }
后面一天居然tm只放了第一题那个鬼畜计算几何dp题的题解。。。就跳过吧
xor
有n个数,求所有2^n个子集异或和中二进制下1的个数的k次方之和,模10^9+7。
1<=n,k<=40,0<=ai<2^40。
怎么一堆40总感觉有点问题...
首先我们发现{a,b,...}与{a^b,b,...}答案一样。
我们考虑将这些数二进制写出来,排成一行一行地,高斯消元。
接下来我们考虑高斯消元后,如果非零的数不超过S,2^S暴力一波即可。
然后我们考虑被约过的(恰好只有一个1的)列,这个显然不止S个,设dp[i][j][k]表示前i行,被约过的列选了j列,剩下的异或起来为k的方案数,一波大暴力即可。
这部分复杂度为40*S*2^(40-S)。
经过反复尝试我们可以发现S=25的时候跑的最快。
不过一如既往还是被卡常了。。。要跑1.3s。。。不管了
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef vector<int> vi; #define fi first #define se second #define fe first int n,k,nc=0; bool one[2333]; ll a[2333],nz[2333],ans=0; ll MOD=1000000007; ll qp(ll a,ll b) { ll ans=1; while(b) { if(b&1) ans=ans*a%MOD; a=a*a%MOD; b>>=1; } return ans; } ll rps[333],rp[2097153]; #define S 25 void force(int c=0,ll s=0) { if(c>=nc) { int a=0; for(int i=1;i<=3;i++) a+=rp[s%2097152], s/=2097152; ans=(ans+rps[a])%MOD; return; } force(c+1,s); force(c+1,s^nz[c]); } int c1[2333]; ll rms[2333]; ll dp[41][41][65537]; ll gans() { ans=0; nc=n; for(int i=0;i<n;i++) nz[i]=a[i]; force(); ll t=ans; nc=0; ans=0; return t; } int main() { freopen("xor.in","r",stdin); freopen("xor.out","w",stdout); scanf("%d%d",&n,&k); for(int i=0;i<=2097152;i++) { int t=i,g=0; while(t) g+=t&1, t>>=1; rp[i]=g; } for(int i=0;i<=300;i++) rps[i]=qp(i,k); for(int i=0;i<n;i++) scanf("%I64d",a+i); ans=0; nc=0; int cp=0,cc=0,qt=0; for(int j=0;j<40;j++) { ll c=1LL<<j; int cur=cp; while(cur<n&&!(a[cur]&c)) ++cur; if(cur>=n) continue; one[j]=1; ++cc; swap(a[cp],a[cur]); for(int i=0;i<n;i++) { if(i!=cp&&(a[i]&c)) a[i]^=a[cp]; } ++cp; } for(int i=0;i<n;i++) if(a[i]) nz[nc++]=a[i]; if(nc<=S) { force(); ans=(ans*qp(2,n-nc)%MOD+MOD)%MOD; cout<<ans<<" "; return 0; } for(int i=0;i<n;i++) { for(int j=0;j<40;j++) { ll c=1LL<<j; if(one[j]) c1[i]+=bool(a[i]&c); else rms[i]=rms[i]*2+bool(a[i]&c); } } dp[0][c1[0]][rms[0]]=1; dp[0][0][0]=1; int ls=1<<(40-cc); for(int i=1;i<n;i++) { memcpy(dp[i],dp[i-1],sizeof(dp[i-1])); for(int j=c1[i];j<=cc;j++) { for(int k=0;k<ls;k++) { dp[i][j][k]+=dp[i-1][j-c1[i]][k^rms[i]]; if(dp[i][j][k]>=MOD) dp[i][j][k]-=MOD; } } } ll ans=0; for(int j=0;j<=cc;j++) { for(int k=0;k<ls;k++) { int co1=j+rp[k]; ans+=qp(co1,::k)*dp[n-1][j][k]%MOD; ans%=MOD; } } ans=(ans%MOD+MOD)%MOD; cout<<ans<<" "; }
kmp
求老司机讲一下弦图染色方案数怎么求啊。。。写到一半写不下去
rng
啊这题有必要截个图
这个题一看就是爬山或者退火嘛。。。
写了一个爬山80分
//By zzq #include <iostream> #include <stdio.h> #include <stdlib.h> #include <algorithm> #include <string.h> #include <time.h> #include <math.h> #include <set> #include <map> using namespace std; int m; typedef double db; char c[2333]; db qfl[2333],qyl[2333]; db qf[2333],qy[2333]; typedef pair<db,int> sta; sta chk(int s) { if(s==0||s==(1<<m)-1) return sta(-233333333,s); int c_f=0,c_y=0; for(int i=0;i<m;i++) { if(s&(1<<i)) ++c_y; else ++c_f; } //(c_f*q_f)/(c_f*q_f+c_y) double gl=0; int t=0; bool x=0; for(int i=0;i<1000;i++) { bool y=s&(1<<(c[i]-'a')); if(!i) { t=1; x=y; continue; } if(x==0) { double gf=(c_f*qf[t])/(c_f*qf[t]+c_y); if(!y) gl+=log(gf); else gl+=log(1-gf); } else { double gy=(c_y*qy[t])/(c_y*qy[t]+c_f); if(y) gl+=log(gy); else gl+=log(1-gy); } if(x!=y) t=0; ++t; x=y; } return sta(gl,s); } int main() { freopen("rng.in","r",stdin); freopen("rng.out","w",stdout); srand(123456); qf[0]=qy[0]=1; for(int i=1;i<=1000;i++) { qfl[i]=qfl[i-1]+log(0.5); qyl[i]=qyl[i-1]+log(2/3.0); qf[i]=qf[i-1]/2; qy[i]=qy[i-1]*2/3; } scanf("%d",&m); for(int p=1;p<=100;p++) { scanf("%s",c); sta ans=chk(0); int rp=0; for(int i=1;i<=10;i++) { sta cur; //gen cur { int s=0; for(int i=0;i<m;i++) if(rand()&1) s|=1<<i; cur=chk(s); } //mountain! int t=0; while(clock()<3.5*i*p) { ++t; int sp=cur.second^(1<<(rand()%m)); sta now=chk(sp); if(now>cur) cur=now, t=0; if(t>=14) break; } ans=max(ans,cur); } ans=max(ans,chk(((1<<m)-1)^ans.second)); int s=ans.second; for(int i=0;i<m;i++) { if(s&(1<<i)) putchar('C'); else putchar('V'); } puts(""); } cerr<<clock()<<" "; }
tourist(题目名称取这个吃枣药丸
小Y来到了一个新的城市旅行。她发现了这个城市的是个n个点简单多边形。她想在多边形内等概率随机选取两点,问这两个点的期望曼哈顿距离。
要求绝对精度1e-3,n<=10^5,坐标为[-10^9,10^9]的整数。
首先在做这题之前我们需要有微积分的基本知识(雾
例如我们要积一个次数不高的函数...但是感觉如果算系数吃枣药丸
如果你确定它是不超过三次的...那么有一个辛普森积分公式可以解决这个问题。
公式:f(x)在[m,n]上的积分为$frac{2f(m)+4f(frac{m+n}{2})+2f(n)}{6}$。
而对于四次、五次,我们可以使用神奇的高斯积分公式。
(此处参考https://en.wikipedia.org/wiki/Gaussian_quadrature)
n个点高斯积分公式的可以积2n-1次的函数!(不是n个点积n次)那么用这个表0~9次的函数都可以这样积分。
用n=3的就足够积五次函数了。
啊扯远了...首先这题x和y可以分开算。我们就考虑计算x好了。
比如P(t)表示随机两个点的线段通过x=t这条直线的概率,那么答案就是对P(t)积分对吧。
那么我们可以发现P(t)=2*左边面积*右边面积/总面积^2(一个在左边,一个在右边,反之亦然)
那我们把x坐标离散,扫描每一段分别积分,那么这时左边面积、右边面积、都是二次函数,乘在一起是四次函数。
Q:为什么左边面积右边面积是二次函数?
A:额因为考虑面积就是平行于y轴的直线在多边形内部的长度的积分,那就是一次函数的积分,二次函数。
我们考虑怎么算这个一边的面积,那我们就是要计算这个被积的一次函数:
这个就很简单了...我们定一个方向为正方向,把这些一次函数扫描维护一下,加加减减一下就行了。(什么?与y轴平行的边?忽略即可)
哦,还要绝对值...这个好办,我们积分的时候把两个端点带进去检验一下...
那么我们算出了一边的面积,只要一波高斯积分即可!
#include <iostream> #include <stdio.h> #include <math.h> #include <string.h> #include <time.h> #include <stdlib.h> #include <string> #include <bitset> #include <vector> #include <set> #include <map> #include <queue> #include <algorithm> #include <sstream> #include <stack> #include <iomanip> using namespace std; #define pb push_back #define mp make_pair typedef pair<int,int> pii; typedef long long ll; typedef double ld; typedef double db; typedef vector<int> vi; #define fi first #define se second #define fe first #define SZ 666666 int n,xs[SZ],ys[SZ]; typedef pair<ld,ld> yc; typedef pair<int,yc> rec; rec rr[SZ]; int xx[SZ]; yc operator + (yc a,yc b) {return yc(a.fi+b.fi,a.se+b.se);} yc operator - (yc a) {return yc(-a.fi,-a.se);} ld Xs[3]={-sqrt(0.6),0,sqrt(0.6)},Ws[3]={5/9.0,8/9.0,5/9.0}; int main() { freopen("tourist.in","r",stdin); freopen("tourist.out","w",stdout); scanf("%d",&n); for(int i=0;i<n;i++) scanf("%d%d",xs+i,ys+i); ld alls=0; for(int i=0;i<n;i++) alls+=xs[i]*(ld)ys[(i+1)%n]-(ld)xs[(i+1)%n]*ys[i]; alls=fabs(alls)/2; ld ans=0; for(int _=0;_<=1;_++) { for(int i=0;i<n;i++) xx[i]=xs[i]; int s1=0; for(int i=0;i<n;i++) { int x=(i+1)%n; if(xs[i]==xs[x]) continue; db k=(ys[x]-ys[i])/double(xs[x]-xs[i]); db b=ys[i]-xs[i]*k; yc cur=yc(k,b); rr[++s1]=rec(xs[i],cur); rr[++s1]=rec(xs[x],-cur); } sort(rr+1,rr+1+s1); sort(xx,xx+n); int xn=unique(xx,xx+n)-xx; yc cur; int s=1; ld ls=0,rs=alls; for(int i=0;i<xn-1;i++) { int l=xx[i],r=xx[i+1]; while(s<=s1&&rr[s].fi==l) cur=cur+rr[s++].se; yc cy=cur; if(cy.fi*l+cy.se<-1e-6) cy=-cy; else if(cy.fi*r+cy.se<-1e-6) cy=-cy; ld area=(cy.fi*l+cy.se+cy.fi*r+cy.se)*ld(r-l)/2; rs-=area; ld X,A=cy.fi/2,B=cy.se,lv=A*l*l+B*l,rv=A*r*r+B*r; //强行人工积分 ld lx=ls-lv,rx=rs+rv,jf=0; for(int i=0;i<3;i++) { X=(r-l)/2.0*Xs[i]+(l+r)/2.0; jf+=Ws[i]*(lx+A*X*X+B*X)*(rx-A*X*X-B*X); } jf=(r-l)*jf/alls/alls; ans+=jf; ls+=area; } for(int i=0;i<n;i++) swap(xs[i],ys[i]); } printf("%.10lf ",ans); }
施工中。。。