DP?
Time Limit: 10000/3000 MS (Java/Others) Memory Limit: 128000/128000 K (Java/Others)
Total Submission(s): 2871 Accepted Submission(s): 894
Problem Description
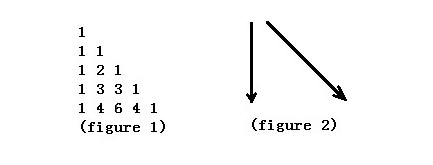
Figure 1 shows the Yang Hui Triangle. We number the row from top to bottom 0,1,2,…and the column from left to right 0,1,2,….If using C(n,k) represents the number of row n, column k. The Yang Hui Triangle has a regular pattern as follows.
C(n,0)=C(n,n)=1 (n ≥ 0)
C(n,k)=C(n-1,k-1)+C(n-1,k) (0<k<n)
Write a program that calculates the minimum sum of numbers passed on a route that starts at the top and ends at row n, column k. Each step can go either straight down or diagonally down to the right like figure 2.
As the answer may be very large, you only need to output the answer mod p which is a prime.
Input
Input
to the problem will consists of series of up to 100000 data sets. For
each data there is a line contains three integers n,
k(0<=k<=n<10^9) p(p<10^4 and p is a prime) . Input is
terminated by end-of-file.
Output
For
every test case, you should output "Case #C: " first, where C indicates
the case number and starts at 1.Then output the minimum sum mod p.
Sample Input
1 1 2
4 2 7
Sample Output
Case #1: 0
Case #2: 5
Author
phyxnj@UESTC
思路:lucas定理;
先打个小范围的表看一下,发现这个和杨辉三角一样是对称的;
然后我们推一下,dp[i][j]=min(dp[i-1][j-1],dp[i-1][j])+ans[i][j];这个可以自己首推递归下,dp[i-1][j-1]是小于dp[i-1][j]的,所以dp[i][j]=dp[i-1][j-1]+ans[i][j];
那么再递归处理dp[i-1][j-1];最后dp[i][j]可以化为dp[i][j]=ans[i-1][j-1]+ans[i-2][j-2]+ans[i-3][j-3]+...ans[i-k][0]+...ans[i-1-k][0]+...ans[0][0];那么最后的ans[d][0]这种等于1的项共有
n-m+1项那么我们在里面拿一项和前面的合并,dp[i][j]=ans[i][j]+ans[i-1][j-1]+ans[i-2][j-2]+...ans[i-k+1][1]+ans[i-k+1][0]+n-m;
dp[n][m]=ans[n+1][m]+n-m;所以前面的组合数用lucas求模,然后需要预处理对各个模的阶乘表。
1 #include<stdio.h> 2 #include<algorithm> 3 #include<iostream> 4 #include<string.h> 5 #include<stdlib.h> 6 #include<queue> 7 #include<map> 8 #include<math.h> 9 using namespace std; 10 typedef long long LL; 11 LL a[10005]; 12 bool prime[10005]; 13 int id[10005]; 14 int biao[2000][10005]; 15 LL quick(LL n,LL m,LL mod); 16 LL lucas(LL n,LL m,LL mod); 17 int main(void) 18 { 19 int i,j,k; 20 LL n,m,mod; 21 for(i=2; i<=1005; i++) 22 if(!prime[i]) 23 for(j=i; (i*j)<=10005; j++) 24 prime[i*j]=true; 25 int tk=0; 26 for(i=2; i<=10005; i++) 27 if(!prime[i]) 28 { 29 id[i]=tk; 30 biao[tk][0]=1; 31 biao[tk][1]=1; 32 for(j=2; j<i; j++) 33 { 34 biao[tk][j]=biao[tk][j-1]*j%i; 35 } 36 tk++; 37 } 38 int __ca=0; 39 while(scanf("%lld %lld %lld",&n,&m,&mod)!=EOF) 40 { 41 __ca++; LL cc=n-m; 42 n+=1; 43 44 m=min(m,cc); 45 LL ask=lucas(m,n,mod); 46 ask=ask+(n-m-1)%mod; 47 ask%=mod; 48 printf("Case #%d: ",__ca); 49 printf("%lld ",ask); 50 } 51 return 0; 52 } 53 LL lucas(LL n,LL m,LL mod) 54 { 55 if(m==0) 56 { 57 return 1; 58 } 59 else 60 { 61 LL nn=n%mod; 62 LL mm=m%mod; 63 if(mm<nn) 64 return 0; 65 else 66 { 67 LL ni=biao[id[mod]][mm-nn]*biao[id[mod]][nn]%mod; 68 ni=biao[id[mod]][mm]*quick(ni,mod-2,mod)%mod; 69 return ni*lucas(n/mod,m/mod,mod); 70 } 71 } 72 } 73 LL quick(LL n,LL m,LL mod) 74 { 75 LL ans=1; 76 while(m) 77 { 78 if(m&1) 79 { 80 ans=ans*n%mod; 81 } 82 n=n*n%mod; 83 m/=2; 84 } 85 return ans; 86 }