D. Artsem and Saunders

Artsem has a friend Saunders from University of Chicago. Saunders presented him with the following problem.

Let [n] denote the set {1, ..., n}. We will also write f: [x] → [y] when a function f is defined in integer points 1, ..., x, and all its values are integers from 1 to y.

Now then, you are given a function f: [n] → [n]. Your task is to find a positive integer m, and two functions g: [n] → [m], h: [m] → [n], such that g(h(x)) = x for all 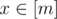, and h(g(x)) = f(x) for all , or determine that finding these is impossible.

Input

The first line contains an integer n (1 ≤ n ≤ 10⁵).

The second line contains n space-separated integers — values f(1), ..., f(n) (1 ≤ f(i) ≤ n).

Output

If there is no answer, print one integer -1.

Otherwise, on the first line print the number m (1 ≤ m ≤ 10⁶). On the second line print n numbers g(1), ..., g(n). On the third line print m numbers h(1), ..., h(m).

If there are several correct answers, you may output any of them. It is guaranteed that if a valid answer exists, then there is an answer satisfying the above restrictions.

Examples

Input

3
1 2 3

Output

3
1 2 3
1 2 3

Input

3
2 2 2

Output

1
1 1 1
2

Input

2
2 1

Output

-1
思路：由h(g(x)) = f(x),假设f(x1) = f(x2);

那么有h(g(x1)) = h(g(x2)),那么我们假设g(x1)!=g(x2),那么就有h中存在两个相等的数，那么g(h(g(x1))) = g(x1),g(h(g(x2))) = g(x2)
就有个g(x1) = g(x2)所以假设不成立，那么h中的数都是不一样的，那么就为f中的不同种类数，m就确定了。
于是确定h(x),那么h(x)有许多的排列，假设x1，x2，h(x1) = a,h(x2) = b,f(y1) = a,f(y2) = b;
通过条件1求出g,h(g(a)) = f(a),h(g(b)) = f(b);-> g(a) = x1,g(b) = x2,那么有h(x1) = f(a),h(x2) = f(b);
那么假设h(x1) = b,h(x2) = a,可以推得g(a) = x2,g(b) = x1,有h(x2) = f(a),h(x1) = f(b),总是可以的f（a）= a，f（b） = b;
所以h的序列任意排序即可，然后求出g，在通过第二个条件验证即可。

#include<stdio.h>
#include<algorithm>
#include<queue>
#include<stdlib.h>
#include<iostream>
#include<string.h>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
set<int>vec;
set<int>::iterator it;
int ans[1000006];
int g[1000006];
int h[1000006];
map<int,int>my;
int main(void)
{
    int n;
    scanf("%d",&n);
    int cn = 0;
    for(int i = 1; i <= n; i++)
        scanf("%d",&ans[i]),vec.insert(ans[i]);
    for(it = vec.begin(); it!=vec.end(); it++)
    {
        h[++cn] = *it;
        my[*it] = cn;
        g[h[cn]] = cn;
    }
    int flag = 0;
    for(int i = 1; i <= n; i++)
    {
        if(g[i] == 0)
        {
            g[i] = my[ans[i]];
        }
        else if(h[g[i]]!=ans[i])
            flag = 1;
    }
    if(flag == 1)
        printf("-1
");
    else
    {
        printf("%d
",cn);
        printf("%d",g[1]);
        for(int i = 2; i <= n; i++)
            printf(" %d",g[i]);
        printf("
");
        printf("%d",h[1]);
        for(int i = 2; i <= cn; i++)
            printf(" %d",h[i]);
    }
    return 0;
}