PAT甲级——A1053 Path of Equal Weight

Given a non-empty tree with root R, and with weight W​i​​ assigned to each tree node T​i​​. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.

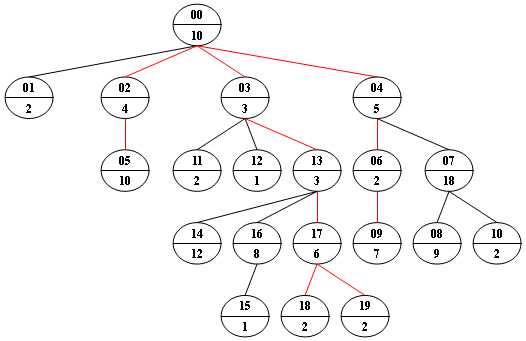
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let's consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0, the number of nodes in a tree, M (<), the number of non-leaf nodes, and 0, the given weight number. The next line contains N positive numbers where W​i​​ (<) corresponds to the tree node T​i​​. Then M lines follow, each in the format:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 00.

Output Specification:

For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.

Note: sequence { is said to be greater than sequence { if there exists 1 such that A​i​​=B​i​​ for ,, and A​k+1​​>B​k+1​​.

Sample Input:

20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19

Sample Output:

10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2

深度遍历

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Node
{
    int val;
    vector<int>child;
}node[101];
int N, M, S;
int path[101];
void DFS(int head, int numNode, int sum)
{
    if (sum > S)
        return;
    if (sum == S)
    {
        if (node[head].child.size() != 0)//不是叶子节点
            return;
        for (int i = 0; i < numNode; ++i)
            cout << node[path[i]].val << (i < numNode - 1 ? " " : "");
        cout << endl;
        return;
    }
    for (int i = 0; i < node[head].child.size(); ++i)
    {
        path[numNode] = node[head].child[i];
        DFS(node[head].child[i], numNode + 1, sum + node[node[head].child[i]].val);
    }
}
int main()
{
    cin >> N >> M >> S;
    for (int i = 0; i < N; ++i)
        cin >> node[i].val;
    int a, b, k;
    for (int i = 0; i < M; ++i)
    {
        cin >> a >> k;
        for (int j = 0; j < k; ++j)
        {
            cin >> b;
            node[a].child.push_back(b);
        }
        sort(node[a].child.begin(), node[a].child.end(),
            [](int a, int b) {return node[a].val > node[b].val; });
    }
    path[0] = 0;
    DFS(0, 1, node[0].val);
    return 0;
}