BFS——279. 完全平方数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12
输出: 3 
解释: 12 = 4 + 4 + 4.

示例 2:

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/perfect-squares

---

思路：

这道题的解题办法有很多，既然先给他归类到了BFS类，就先用BFS的思路来解题。（动态规划中还要再做一次）

遍历完第一层再遍历第二层再第三层。。。

那么第二层，第三层分别是什么东西，怎么来的呢？

再此之前我们要先得到一个集合，用来存储给定的n之前的所有的平方数

以13为例，那么13前面的平方数就有{1 ，4 ，9}

那么第二层的内容就是第一个13 - 1 = 12；第二个 13 - 4 = 9； 13 - 9 = 4；

当观察到的第二个和第三个，减去平方数的差值，他还是一个平方数，13 - 4 = 9，9就是一个平方数

那么好，这就说明找到了，那么就返回他的层次level就行了。

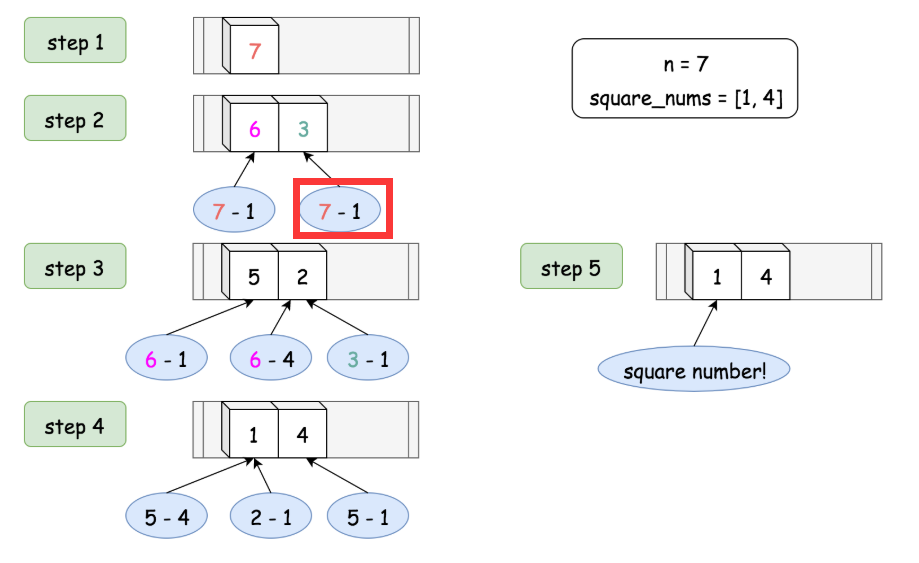
 这是官方的图，我框起来的地方是有错误的应该是 7 - 4 = 3，官方失误最为致命，知道就好了，嘘~

找到step4才出现了第一个和小于7的平方数集合{1,4}中相同的数字：1

也就是说找到了第四层才发现，所以要返回leve = 4；那么验证一下，7 = 4 + 1 + 1 +1，四层，没问题！

class Solution {
    public int numSquares(int n) {
        //第一步：定义一个动态数组来存储n之前的所有平方数
        List<Integer> square_num = new ArrayList<>();
        for (int i = 1; i * i <= n; i++) {
            square_num.add(i * i);
        }
        //第二步：定义一个动态数组来存放当前的层次有哪些数据
        //定义一个level来记录层次
        List<Integer> queue = new ArrayList<Integer>();
        int level = 0;
        queue.add(n);
        while (queue.size() > 0){
            level ++;
            List<Integer> next_queue = new ArrayList<Integer>();
            for (Integer a : queue){
                for (Integer b : square_num){
                    if (a.equals(b)){
                        //说明这个数他就和平方数相同了，返回层数
                        return level;
                    }else if (a <= b){
                        break;
                    }else {
                        next_queue.add(a - b);
                    }
                }
            }
            queue = next_queue;
        }
        return level;
    }
}

需要好好的理解一下！

另外再记录一种平方数记录算法

private List<Integer> generateSquares(int n) {
    List<Integer> squares = new ArrayList<>();
    int square = 1;
    int diff = 3;
    while (square <= n) {
        squares.add(square);
        square += diff;
        diff += 2;
    }
    return squares;
}