HDU 4386 Quadrilateral（四边形的海伦公式的应用）

　　题目链接：http://acm.hust.edu.cn/vjudge/contest/view.action?cid=115760#problem/G

　　题目大意是给出四条边，问能否组成一个四边形，如果可以的话输出最大的四边形的面积，否则输出-1。

　　判断能否组成四边形和三角形差不多，只要满足任意三条边大于第四条边即可。

　　而对于计算面积，仓鼠学长给的方法是找两条边，然后二分它们的夹角找出最小的面积即可（因为四条边确定了，再确定一个夹角那么这个四边形的面积也就确定了）。然而还有更快的方法。

　　根据四边形的海伦公式，S<=sqrt((p-a)*(p-b)*(p-c)*(p-d))，（p是四边形的半周长）。那么答案就很显然了- -。。（幻神这题秒过真是厉害。。）

　　证明方法如下：

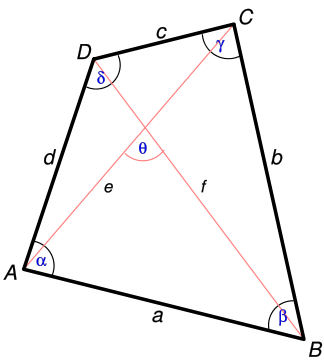
利用三角形的各种公式就可以证明出来了，要注意的是，S最大的条件是对角的和是180°。

　　下面给出AC代码：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <math.h>
#include <string.h>
using namespace std;
int dp[50][20];
int num[50];
int main()
{
    int T;
    scanf("%d",&T);
    for(int i=1;i<=T;i++)
    {
        printf("Case %d: ",i);
        double a,b,c,d;
        cin>>a>>b>>c>>d;
        double p = (a+b+c+d)/2;
        if(p<=a||p<=b||p<=c||p<=d) puts("-1");
        else printf("%f
",sqrt((p-a)*(p-b)*(p-c)*(p-d)));
    }
}

　　另外，在这里再回顾一下三角形的海伦公式，有点区别：S=sqrt(p*(p-a)*(p-b)*(p-c))，（p同样是半周长）。