做到这里以后,总算是觉得tarjan算法已经有点入门了。
这题的题意是,给出若干个点和若干条边连接他们,在这个无向图中,问至少增加多少条边可以使得这个图变成边双联通图(即任意两点间都有至少两条没有重复边的路径可以到达,可以经过同一个点。这个条件等价于每一条边都至少在一个环中)。
方法:将无向图缩点以后,找出那些度为1的点的个数cnt,那么答案就是(cnt+1)/2。这么一看,好像就是缩点以后使它变成强连通图的意思?大概强连通图是有向图才有的名词吧。。
和有向图缩点类似,只要把if(!belong[v])改成if(v != fa)即可,这样,就可以防止同一条边的方向性关系了,而a到b如果是间接到达的话,是没有问题的。还有,通过这题,我明白了为什么tarjan算法里面有一个是用dfn来更新的了。这里来回顾一下:找割点或者桥的时候有low[v]和dfn[u]的比较,如果都是用low更新的话,那么low可能会变小导致漏掉割点或者桥的情况。举割点那篇中的图当例子:http://www.cnblogs.com/zzyDS/p/5629021.html 如这个图,
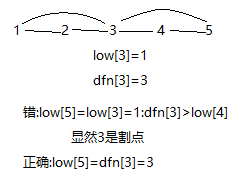
图(v,e)点为1,2,3,4,5,边有(1,2),(2,3),(1,3),(3,4),(4,5),(3,5),令1为树根。显然3为割点。不妨假设搜索顺序是(1,2),(2,3),(3,1),(3,4),(4,5),(5,3),搜索到(3,1)的时候,更新low[3] = dfn[1] = 1,然后搜索(3,4)、(4,5),(5,3),发现3已经遍历,那么如果此时采用low[u] = min(low[u], low[v])的话,会更新low[5] = low[3] = 1,回溯到4,low[4] = low[5] = 1,回溯到3,low[3] = low[4] = 1,然后比较发现low[4] < dfn[3],判断出3不是割点,算法错误。反正以后都用dfn更新应该就对了- -还有一点想说的是,用dfn的好处在于,不需要belong数组了,只要low一样的那么他们缩点以后都属于一个点(这个说法是错误的!上面这个图就是反例,上面那个图缩点以后还是只有一个点了,所以还是老老实实的用belong数组吧)。
另外,这题比较有意思的地方在于,题目给定,两个点之间如果有重边,只算一条。那么就引发了一大堆有意思的讨论了。
先给出最初的代码(WA的,因为没判断重边):

1 #include <stdio.h> 2 #include <stack> 3 #include <algorithm> 4 #include <string.h> 5 #include <vector> 6 using namespace std; 7 8 const int N = 5000+5; 9 10 stack<int> S; 11 int dfs_clock; 12 int dfn[N]; 13 int low[N]; 14 vector<int> G[N]; 15 int n,r; 16 int du[N]; 17 18 void dfs(int u,int fa) 19 { 20 dfn[u] = low[u] = ++dfs_clock; 21 for(int i=0;i<G[u].size();i++) 22 { 23 int v = G[u][i]; 24 if(!dfn[v]) 25 { 26 dfs(v,u); 27 low[u] = min(low[u],low[v]); 28 } 29 else if(v != fa) 30 { 31 low[u] = min(low[u],dfn[v]); 32 } 33 } 34 } 35 36 void solve() 37 { 38 for(int i=1;i<=n;i++) 39 { 40 if(!dfn[i]) dfs(i,-1); 41 } 42 43 for(int i=1;i<=n;i++) 44 { 45 for(int j=0;j<G[i].size();j++) 46 { 47 int v = G[i][j]; 48 if(low[i]!=low[v]) du[low[i]]++; 49 } 50 } 51 52 int cnt=0; 53 for(int i=1;i<=dfs_clock;i++) if(du[i]==1) cnt++; 54 printf("%d ",(cnt+1)/2); 55 } 56 57 void init() 58 { 59 for(int i=1;i<=n;i++) G[i].clear(); 60 dfs_clock=0; 61 memset(dfn,0,sizeof(dfn)); 62 memset(du,0,sizeof(du)); 63 } 64 65 int main() 66 { 67 while(scanf("%d%d",&n,&r)==2) 68 { 69 init(); 70 71 for(int i=1;i<=r;i++) 72 { 73 int u,v; 74 scanf("%d%d",&u,&v); 75 G[u].push_back(v); 76 G[v].push_back(u); 77 } 78 solve(); 79 } 80 return 0; 81 }
然后由于这题给的边是5000,可以用邻接矩阵来做,但是要注意用bool数组,不然超内存。代码如下:

1 #include <stdio.h> 2 #include <stack> 3 #include <algorithm> 4 #include <string.h> 5 #include <vector> 6 using namespace std; 7 8 const int N = 5000+5; 9 10 int dfs_clock; 11 int dfn[N]; 12 int low[N]; 13 int n,r; 14 int du[N]; 15 bool mp[N][N]; 16 17 void dfs(int u,int fa) 18 { 19 dfn[u] = low[u] = ++dfs_clock; 20 for(int i=1;i<=n;i++) 21 { 22 if(!mp[u][i]) continue; 23 if(!dfn[i]) 24 { 25 dfs(i,u); 26 low[u] = min(low[u],low[i]); 27 } 28 else if(i != fa) 29 { 30 low[u] = min(low[u],dfn[i]); 31 } 32 } 33 } 34 35 void solve() 36 { 37 for(int i=1;i<=n;i++) 38 { 39 if(!dfn[i]) dfs(i,-1); 40 } 41 42 for(int i=1;i<=n;i++) 43 { 44 for(int j=1;j<=n;j++) 45 { 46 if(!mp[i][j]) continue; 47 if(low[i]!=low[j]) du[low[i]]++; 48 } 49 } 50 51 int cnt=0; 52 for(int i=1;i<=dfs_clock;i++) if(du[i]==1) cnt++; 53 printf("%d ",(cnt+1)/2); 54 } 55 56 void init() 57 { 58 memset(mp,0,sizeof(mp)); 59 dfs_clock=0; 60 memset(dfn,0,sizeof(dfn)); 61 memset(du,0,sizeof(du)); 62 } 63 64 int main() 65 { 66 while(scanf("%d%d",&n,&r)==2) 67 { 68 init(); 69 70 for(int i=1;i<=r;i++) 71 { 72 int u,v; 73 scanf("%d%d",&u,&v); 74 if(mp[u][v]) continue; 75 mp[u][v]=mp[v][u]=1; 76 } 77 solve(); 78 } 79 return 0; 80 }
然后要判重的话,可以用大力学长的set法,把边用pair记录然后全部丢进set里面用find来查找即可,代码如下:

1 #include<iostream> 2 #include<cstdio> 3 #include<string> 4 #include<cstring> 5 #include<map> 6 #include<queue> 7 #include<stack> 8 #include<algorithm> 9 #include<cmath> 10 #include<set> 11 #include<vector> 12 using namespace std; 13 typedef long long ll; 14 typedef long long LL; 15 #define MP make_pair 16 #define PII pair<int,int> 17 #define PFI pair<double,int> 18 #define F first 19 #define S second 20 #define lson l,mid,rt<<1 21 #define rson mid+1,r,rt<<1|1 22 const int INF = 0x7f7f7f7f; 23 const int MOD = 100000007; 24 const double eps = 1e-8; 25 const int maxn = 100000 + 50; 26 27 const int N = 5000 + 50; 28 int n,m; 29 vector<vector<int> > G(N); 30 int scc_cnt,dfs_clock,belong[N],dfn[N],low[N]; 31 bool instack[N]; 32 stack<int> S; 33 set<pair<int,int> > st; 34 void dfs(int u,int fa){ 35 low[u] = dfn[u] = ++ dfs_clock; 36 S.push(u); 37 for(int i = 0 ; i < G[u].size() ; i ++){ 38 int v = G[u][i]; 39 if(v == fa) continue; // 无向图 a-b: 防止b访问a(父亲) 40 if(!dfn[v]){ 41 dfs(v,u); 42 low[u] = min(low[u],low[v]); 43 }else if(!belong[v]){ 44 low[u] = min(low[u],dfn[v]); 45 } 46 } 47 if(low[u] == dfn[u]){ 48 scc_cnt ++; 49 for(;;){ 50 int x = S.top(); S.pop(); 51 belong[x] = scc_cnt; // 缩点。 52 if(x == u) break; 53 } 54 } 55 } 56 void scc(){ 57 scc_cnt = dfs_clock = 0; 58 memset(belong,0,sizeof(belong)); 59 memset(dfn,0,sizeof(dfn)); 60 memset(low,0,sizeof(low)); 61 memset(instack,false,sizeof(instack)); 62 while(!S.empty()) S.pop(); 63 for(int i = 1 ; i <= n ; i ++){ 64 if(!dfn[i]) dfs(i,-1); 65 } 66 int deg[N]; 67 memset(deg,0,sizeof(deg)); 68 for(int i = 1 ; i <= n ; i ++){ 69 for(int j = 0 ; j < G[i].size() ; j ++){ 70 int v = G[i][j]; 71 if(belong[i] != belong[v]){ 72 deg[ belong[i] ] ++; 73 deg[ belong[v] ] ++; 74 } 75 } 76 } 77 int cnt = 0; 78 for(int i = 1 ; i <= n ; i++){ 79 if(deg[i] / 2 == 1) cnt ++; 80 } 81 cout << (cnt + 1) / 2 << endl; 82 } 83 int main(){ 84 while(scanf("%d%d",&n,&m) != EOF){ 85 for(int i = 0 ; i <= n ; i ++) G[i].clear(); 86 st.clear(); 87 for(int i = 0 ; i < m ; i ++){ 88 int u,v; 89 scanf("%d%d",&u,&v); 90 // 判重边。 91 if(st.find(MP(u,v)) != st.end()) continue; 92 if(st.find(MP(v,u)) != st.end()) continue; 93 st.insert(MP(u,v)); 94 st.insert(MP(v,u)); 95 G[u].push_back(v); 96 G[v].push_back(u); 97 } 98 scc(); 99 } 100 return 0; 101 }
最后,我想,既然要判重,干脆不用vector了,直接用set吧- -!代码如下:

1 #include <stdio.h> 2 #include <stack> 3 #include <algorithm> 4 #include <string.h> 5 #include <vector> 6 #include <set> 7 using namespace std; 8 9 const int N = 5000+5; 10 11 stack<int> S; 12 int dfs_clock; 13 int dfn[N]; 14 int low[N]; 15 set<int> G[N]; 16 int n,r; 17 int du[N]; 18 19 void dfs(int u,int fa) 20 { 21 dfn[u] = low[u] = ++dfs_clock; 22 for(set<int>::iterator it=G[u].begin();it!=G[u].end();it++) 23 { 24 int v = *it; 25 if(!dfn[v]) 26 { 27 dfs(v,u); 28 low[u] = min(low[u],low[v]); 29 } 30 else if(v != fa) 31 { 32 low[u] = min(low[u],dfn[v]); 33 } 34 } 35 } 36 37 void solve() 38 { 39 for(int i=1;i<=n;i++) 40 { 41 if(!dfn[i]) dfs(i,-1); 42 } 43 44 for(int i=1;i<=n;i++) 45 { 46 for(set<int>::iterator it=G[i].begin();it!=G[i].end();it++) 47 { 48 int v = *it; 49 if(low[i]!=low[v]) du[low[i]]++; 50 } 51 } 52 53 int cnt=0; 54 for(int i=1;i<=dfs_clock;i++) if(du[i]==1) cnt++; 55 printf("%d ",(cnt+1)/2); 56 } 57 58 void init() 59 { 60 for(int i=1;i<=n;i++) G[i].clear(); 61 dfs_clock=0; 62 memset(dfn,0,sizeof(dfn)); 63 memset(du,0,sizeof(du)); 64 } 65 66 int main() 67 { 68 while(scanf("%d%d",&n,&r)==2) 69 { 70 init(); 71 72 for(int i=1;i<=r;i++) 73 { 74 int u,v; 75 scanf("%d%d",&u,&v); 76 G[u].insert(v); 77 G[v].insert(u); 78 } 79 solve(); 80 } 81 return 0; 82 }
