2016 Multi-University Training Contest 2 部分题解

　　1009，直接贪心，只要让后面的尽量小，第一位和第二位尽量大即可。

　　

　　1011，直接统计奇数的字母的个数，然后用偶数的个数平均分配到它们上面即可。代码如下：

#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std;

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        int odd = 0, even = 0;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            int t;
            scanf("%d",&t);
            if(t % 2)
            {
                odd ++;
                even += (t - 1) / 2;
            }
            else even += t / 2;
        }
        if(odd == 0)
        {
            printf("%d
",even << 1);
        }
        else
        {
            printf("%d
",even / odd * 2 + 1);
        }
    }
}

　　1001，用二次函数做即可，把阿尔法看做一个未知数。分析过程如下：

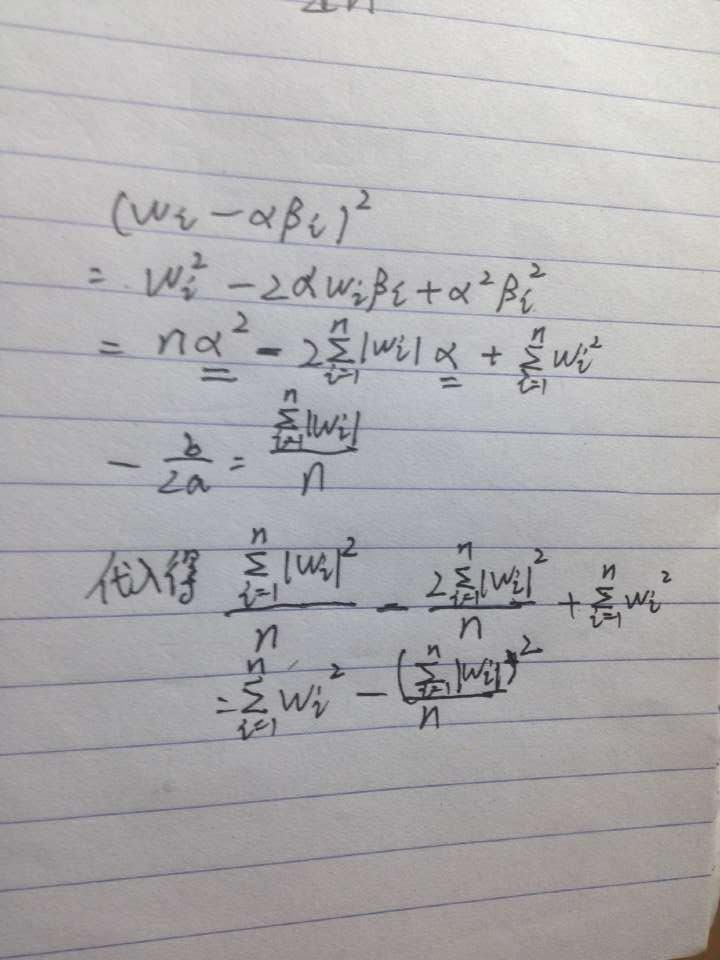
代码如下：

#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std;
typedef long long ll;

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        ll sum = 0, sum2 = 0;
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            int t;
            scanf("%d",&t);
            if(t<0) t = -t; // 全部值都变正
            sum += t;
            sum2 += (ll)t*t;
        }
        sum *= sum;
        if(sum == 0)
        {
            printf("I64%d/%d
",sum2,1);
            continue;
        }
        ll gd = __gcd(sum,(ll)n);
        if(gd > 1)
        {
            sum /= gd;
            n /= gd;
        }
        sum2 *= n;
        sum2 -= sum;
        if(sum2 == 0)
        {
            printf("%d/%d
",0,1);
            continue;
        }
        gd = __gcd(sum2,(ll)n);
        if(gd > 1)
        {
            sum2 /= gd;
            n /= gd;
        }
        printf("%I64d/%d
",sum2,n);
    }
}

　　1012，题意是匹配串和原串去匹配，原串的相应区间可以对某些位置进行操作。设位置x是可以操作的，那么x和它下一个位置进行交换；同时，两个x之间的间隔必须大于等于1。直接暴力即可，代码如下：

#include <bits/stdc++.h>
using namespace std;

char s[(int)1e5+5],t[5000+5];
char ans[(int)1e5+5];
int n,m;

bool isok(int pos)
{
    int j = 1;
    for(int i=pos;i<=pos+m-1;)
    {
        if(s[i] == t[j])
        {
            i++,j++;
        }
        else
        {

            if(i == pos+m-1) return false;
            if(s[i] != t[j+1] || s[i+1] != t[j]) return false;
            else i += 2,j += 2;
        }
    }
    return true;
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        scanf("%s",s+1);
        scanf("%s",t+1);
        for(int i=1;i<=n;i++) ans[i] = '0';
        for(int i=1;i+m-1<=n;i++)
        {
            if(isok(i)) ans[i] = '1';
            else ans[i] = '0';
        }
        for(int i=1;i<=n;i++)
        {
            printf("%c",ans[i]);
        }
        puts("");
    }
}

 　　

　　1005，找出共线的点的集合（集合内点的个数大于等于2，可以是重点）。最初的做法是，找出所有的直线方程，统计这上面的点的个数，然后这条线上的集合的个数就是C(2,m)+C(3,m)+...+C(m,m) = 2^m - m - 1。但是我们实现用了大量的map，可能是因为这一点，超时了。TLE的代码如下：

#include<cstdio>
#include<cstring>
#include<iostream>
#include <map>
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = (int)1e9 + 7;
//const ll p = 257;

struct line
{
    ll a,b,c;
    bool operator <(const line & A) const
    {
        return a==A.a?  b==A.b?c<A.c:b<A.b :a<A.a;
    }
};
struct point
{
    ll x,y;
    bool operator < (const point & A) const
    {
        return x==A.x ? y<A.y :x<A.x;
    }

}p[1000+5];

ll qpow(ll x,ll y)
{
    ll ans = 1;
    while(y)
    {
        if(y&1) ans = ans * x % mod;
        y >>= 1;
        x = (x*x) % mod;
    }
    return ans;
}

map<line,ll> M;
map<point,ll> M2;
map<line,ll> M3;
//set<point> S;

bool isequel(point a,point b)
{
    if(a.x==b.x && a.y==b.y) return 1;
    return 0;
}

void get(ll &a,ll &b,ll &c,point p1,point p2)
{
    ll x1 = p1.x,y1 = p1.y;
    ll x2 = p2.x,y2 = p2.y;
    c = x1 - x2;
    a = y1 - y2;
    b = x1*y2-y1*x2;
}

ll getn(ll now)
{
    for(ll i = 1 ;;i++)
    {
        if(i*(i+1)/2 == now) return i+1;
    }
}

void modify(ll& a , ll & b, ll &c)
{
    if(a==0 && b == 0) {c=1;return;}
    if(b==0 && c == 0) {a=1;return;}
    if(a==0 && c == 0) {b=1;return;}
    if(a && b && c)
    {
        int gd = __gcd(a,__gcd(b,c));
        a /= gd;
        b /= gd;
        c /= gd;
    }
    else
    {
        if(a==0)
        {
            int gd = __gcd(b,c);
            b /= gd;
            c /= gd;
        }
        else if(b==0)
        {
            int gd = __gcd(a,c);
            a /= gd;
            c /= gd;
        }
        else if(c==0)
        {
            int gd = __gcd(a,b);
            a /= gd;
            b /= gd;
        }
    }
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        M.clear();
        M2.clear();
        M3.clear();
        //S.clear();
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
        {
            ll x,y;
            scanf("%I64d%I64d",&x,&y);
            p[i] = (point){x,y};
            M2[p[i]] ++;
        }

        for(map<point,ll>::iterator it=M2.begin();it!=M2.end();it++)
        {
            map<point,ll>::iterator it2 = it;
            it2++;
            for(;it2!=M2.end();it2++)
            {
                //if(isequel((*it).first,(*it2).first)) continue;
                ll a,b,c;
                get(a,b,c,(*it).first,(*it2).first);
                modify(a,b,c);
                M[(line){a,b,c}] += (*it).second + (*it2).second;
                M3[(line){a,b,c}] ++;
                //S.insert(p[i]);
                //printf("%d %d  %d !!
",i,j,M[(line){a,b,c}]);
            }
        }

        ll ans = 0;

        for(map<line,ll>::iterator it = M.begin();it!=M.end();it++)
        {
            ll nownow = (*it).second;
            //cout << now <<"!!"<<endl;
            //ll n = now / 2;
            map<line,ll>::iterator  itt = M3.find((*it).first);
            ll now = ((*itt).second);
            //ll now = M3.second;
            ll n = getn(now);
            ll nn = nownow/(n-1);
            ans += (qpow(2,nn)-nn-1);
            ans %= mod;
        }
        for(map<point,ll>::iterator it = M2.begin();it!=M2.end();it++)
        {
            ll now = (*it).second;
            if(now<=1) continue;
            ans += (qpow(2,now)-now-1);
        }

        cout << ans <<endl;

    }
    return 0;
}

/*

    5
    0 1
    0 0
    0 0
    0 1
    0 2
*/

看了标程以后觉得他的方法很好。大概是这样子的：先对所有的点按照x，y的大小排序，然后对每一个点，算出包含了这个点的的集合的个数。具体见代码和注释：

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 1000 + 50;
const int mod = (int)1e9 + 7;

struct point
{
    int x, y;
    point() {}
    point(int _x, int _y): x(_x), y(_y) {}
    point operator - (const point & temp) const
    {
        return point(x - temp.x, y - temp.y); 
    }
    bool operator < (const point & temp) const
    {
        return x < temp.x || (x == temp.x && y < temp.y);
    }
    bool operator == (const point & temp) const
    {
        return x == temp.x && y == temp.y;
    }
    void reduce()
    {
        int g = __gcd(abs(x), abs(y));
        if(g) {x /= g; y /= g;}
    }
} p[N], Q[N];

int pw[N];
void init()
{
    pw[0] = 1;
    for(int i = 1; i < N; i++) pw[i] = pw[i-1] * 2 % mod;
}

void update(int &x, int y)
{
    x += y;
    if(x >= mod) x -= mod;
}

void run()
{
    int n;scanf("%d", &n);
    int ans = 0;
    for(int i = 1; i <= n; i++) scanf("%d%d",&p[i].x, &p[i].y);
    // 先要对所有点排序，不然共线向量会有正负的区别
    sort(p + 1, p + 1 + n);
    for(int i = 1; i <= n; i++) 
    {
        int cnt = 0, tot = 0;
        // cnt 是除了i这个点以外的重点的个数
        // m是 这个点位置以外的点的个数
        for(int j = i + 1; j <= n; j++)
        {
            if(p[i] == p[j]) cnt++;
            else Q[++tot] = p[j] - p[i]; // Q 放的是向量
        }
        update(ans, pw[cnt] - 1); // 这里是对重点们形成集合的贡献
        // 计算方式是选出i这个点，之后从剩下的cnt这么多个点中选出至少一个的种类数
        // 那么，贡献就是C(1,cnt)+C(2,cnt)+...+C(cnt,cnt) = 2^cnt - 1

        for(int j = 1; j <= tot; j++) Q[j].reduce();
        sort(Q + 1, Q + 1 + tot);
        for(int x = 1, y; x <= tot; x = y)
        {
            for(y = x; y <= tot && Q[x] == Q[y]; y++) ;
            // y 出来的时候已经是 Q[x] != Q[y] 了，因此 y-x 正好是这一个角度上其他的点的个数
            // 这时候，对答案的贡献是，从除了i这个点以外的重点中选出任意个数的点的种类数
            // 和从这个角度上的其他点中选出至少1个点的种类数的乘积
            update(ans, 1LL * pw[cnt] * (pw[y - x] - 1) % mod); 
        }
    }
    printf("%d
", ans);
}

int main()
{
    init();
    int T;scanf("%d", &T);
    while(T--) run();
    return 0;
}