传送门
考查题型 搜索 字符串 模拟 dp
T1 神经网络
题目背景
人工神经网络(Artificial Neural Network)是一种新兴的具有自我学习能力的计算系统,在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向,兰兰同学在自学了一本神经网络的入门书籍后,提出了一个简化模型,他希望你能帮助他用程序检验这个神经网络模型的实用性。
题目描述
在兰兰的模型中,神经网络就是一张有向图,图中的节点称为神经元,而且两个神经元之间至多有一条边相连,下图是一个神经元的例子:
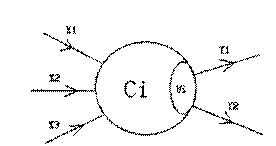
神经元〔编号为1)
图中,X1―X3是信息输入渠道,Y1-Y2是信息输出渠道,C1表示神经元目前的状态,Ui是阈值,可视为神经元的一个内在参数。
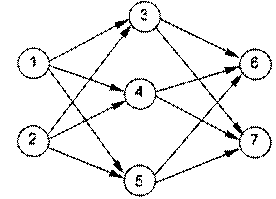
神经元按一定的顺序排列,构成整个神经网络。在兰兰的模型之中,神经网络中的神经无分为几层;称为输入层、输出层,和若干个中间层。每层神经元只向下一层的神经元输出信息,只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。
兰兰规定,Ci服从公式:(其中n是网络中所有神经元的数目)
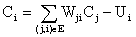
公式中的Wji(可能为负值)表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时,该神经元处于兴奋状态,否则就处于平静状态。当神经元处于兴奋状态时,下一秒它会向其他神经元传送信号,信号的强度为Ci。
如此.在输入层神经元被激发之后,整个网络系统就在信息传输的推动下进行运作。现在,给定一个神经网络,及当前输入层神经元的状态(Ci),要求你的程序运算出最后网络输出层的状态。
输入输出格式
输入格式:
输入文件第一行是两个整数n(1≤n≤100)和p。接下来n行,每行两个整数,第i+1行是神经元i最初状态和其阈值(Ui),非输入层的神经元开始时状态必然为0。再下面P行,每行由两个整数i,j及一个整数Wij,表示连接神经元i、j的边权值为Wij。
输出格式:
输出文件包含若干行,每行有两个整数,分别对应一个神经元的编号,及其最后的状态,两个整数间以空格分隔。仅输出最后状态大于零的输出层神经元状态,并且按照编号由小到大顺序输出!
若输出层的神经元最后状态均为 0,则输出 NULL。
输入输出样例
5 6 1 0 1 0 0 1 0 1 0 1 1 3 1 1 4 1 1 5 1 2 3 1 2 4 1 2 5 1
题解
(1)正向建边dfs每一层的点
反向建边从第二层开始推每个点的状态
这样做完美避过所有坑点 一次AC
#include<iostream> #include<cstdio> #define N 101 using namespace std; int n,p,x,cc,y,zz,cnt,flag,zsumedge,fsumedge; int c[N],u[N],rd[N],cd[N],ceng[N],z[N][N],fa[N],zhead[N],fhead[N]; struct E1{ int x,y,z,nxt; E1(int x=0,int y=0,int z=0,int nxt=0): x(x),y(y),z(z),nxt(nxt){} }zedge[N<<1]; struct E2{ int x,y,z,nxt; E2(int x=0,int y=0,int z=0,int nxt=0): x(x),y(y),z(z),nxt(nxt){} }fedge[N<<1]; void zadd(int x,int y,int z){ zedge[++zsumedge]=E1(x,y,z,zhead[x]); zhead[x]=zsumedge; } void fadd(int x,int y,int z){ fedge[++fsumedge]=E2(x,y,z,fhead[x]); fhead[x]=fsumedge; } void dfs(int k){ ceng[k]=ceng[fa[k]]+1; z[ceng[k]][++z[ceng[k]][0]]=k; cc=max(cc,ceng[k]); for(int i=zhead[k];i;i=zedge[i].nxt){ int v=zedge[i].y; if(fa[k]!=v){ fa[v]=k; dfs(v); } } } int main(){ scanf("%d%d",&n,&p); for(int i=1;i<=n;i++){ scanf("%d%d",&c[i],&u[i]); } for(int i=1;i<=p;i++){ scanf("%d%d%d",&x,&y,&zz); cd[x]++;rd[y]++; zadd(x,y,zz);fadd(y,x,zz); } for(int i=1;i<=n;i++) if(!rd[i])dfs(i); for(int s=2;s<=cc;s++){ for(int i=1;i<=z[s][0];i++){ int v=z[s][i];cnt=0; for(int j=fhead[v];j;j=fedge[j].nxt){ int vv=fedge[j].y; if(c[vv]>0)cnt+=(fedge[j].z*c[vv]); } c[v]=cnt-u[v]; } } for(int i=1;i<=n;i++){ if(cd[i]==0&&c[i]>0){ flag=1;printf("%d %d ",i,c[i]); } } if(flag==0)printf("NULL "); return 0; }
(2)宽搜+模拟
#include<iostream> #include<cstdio> #define mx 103 using namespace std; int n,p,x,y,z,sumedge,hed=1,tail,flag; int head[mx],h[mx],q[mx],c[mx],u[mx],inq[mx]; struct Edge{ int x,y,z,nxt; Edge(int x=0,int y=0,int z=0,int nxt=0): x(x),y(y),z(z),nxt(nxt){} }edge[mx]; void add(int x,int y,int z){ edge[++sumedge]=Edge(x,y,z,head[x]); h[x]=sumedge; head[x]=sumedge; } void bfs(){ while(hed<=tail){ int now=q[hed++]; if(c[now]<=0)continue; for(int i=head[now];i;i=edge[i].nxt){ int v=edge[i].y; c[v]+=(c[now]*edge[i].z); if(!inq[v]){q[++tail]=v;c[v]-=u[v];inq[v]=1;} } } } int main(){ scanf("%d%d",&n,&p); for(int i=1;i<=n;i++){ scanf("%d%d",&c[i],&u[i]); if(c[i])q[++tail]=i,inq[i]=1; } for(int i=1;i<=p;i++){ scanf("%d%d%d",&x,&y,&z); add(x,y,z); } bfs(); for(int i=1;i<=n;i++) if(h[i]==0)if(c[i]>0){printf("%d %d ",i,c[i]);flag=1;} if(flag==0)printf("NULL "); return 0; }
T2 侦探推理
题目描述
明明同学最近迷上了侦探漫画《柯南》并沉醉于推理游戏之中,于是他召集了一群同学玩推理游戏。游戏的内容是这样的,明明的同学们先商量好由其中的一个人充当罪犯(在明明不知情的情况下),明明的任务就是找出这个罪犯。接着,明明逐个询问每一个同学,被询问者可能会说:

证词中出现的其他话,都不列入逻辑推理的内容。
明明所知道的是,他的同学中有N个人始终说假话,其余的人始终说真。
现在,明明需要你帮助他从他同学的话中推断出谁是真正的凶手,请记住,凶手只有一个!
输入输出格式
输入格式:
输入由若干行组成,第一行有三个整数,M(1≤M≤20)、N(1≤N≤M)和P(1≤P≤100);M是参加游戏的明明的同学数,N是其中始终说谎的人数,P是证言的总数。接下来M行,
每行是明明的一个同学的名字(英文字母组成,没有主格,全部大写)。
往后有P行,每行开始是某个同学的名宇,紧跟着一个冒号和一个空格,后面是一句证词,符合前表中所列格式。证词每行不会超过250个字符。
输入中不会出现连续的两个空格,而且每行开头和结尾也没有空格。
输出格式:
如果你的程序能确定谁是罪犯,则输出他的名字;如果程序判断出不止一个人可能是罪犯,则输出 Cannot Determine;如果程序判断出没有人可能成为罪犯,则输出 Impossible。
输入输出样例
3 1 5 MIKE CHARLES KATE MIKE: I am guilty. MIKE: Today is Sunday. CHARLES: MIKE is guilty. KATE: I am guilty. KATE: How are you??
题解 字符串+模拟
#include<cstdio> #include<map> #include<iostream> #include<string> using namespace std; int n,m,p,s[22][102],l[22],d[22][102],day[22][102],gu[22]; map<string,int>t; map<int,string>h; string u,v[102],g[102],q[102],bb; int main() { scanf("%d%d%d",&m,&n,&p); for (int i=0;i<m;i++) {cin>>u;t[u]=i+1;h[i+1]=u;} for (int i=0;i<p;i++) { int y,ll=1;u="";while(u[ll-1]!='.' && u[ll-1]!='?' && u[ll-1]!='!') {cin>>bb;if (ll>1)u+=' ';u+=bb;ll=u.length();} for (int j=0;j<ll&&u[j]!=':';j++) {v[i]+=u[j];y=j;} int jj=t[v[i]],b=-1,nn=0,uu=0; for (int j=y+3;j<ll;j++) { if (!uu)g[i]+=u[j];else q[i]+=u[j]; if (!nn && !uu && u[j+1]==' ')for (int k=1;k<=m;k++)if (h[k]==g[i]){b=k;break;} if (b!=-1 && !nn && !uu){g[i]=u[j+2];j+=2;nn=1;} if (g[i]=="Today is ")uu=1; } if (g[i]=="I am guilty.")s[jj][l[jj]++]=1; if (g[i]=="I am not guilty.")s[jj][l[jj]++]=2; if (g[i]=="is guilty."){s[jj][l[jj]]=3;d[jj][l[jj]++]=b;} if (g[i]=="is not guilty."){s[jj][l[jj]]=4;d[jj][l[jj]++]=b;} if (g[i]=="Today is ") { s[jj][l[jj]]=5; if (q[i]=="Monday.")day[jj][l[jj]++]=1; if (q[i]=="Tuesday.")day[jj][l[jj]++]=2; if (q[i]=="Wednesday.")day[jj][l[jj]++]=3; if (q[i]=="Thursday.")day[jj][l[jj]++]=4; if (q[i]=="Friday.")day[jj][l[jj]++]=5; if (q[i]=="Saturday.")day[jj][l[jj]++]=6; if (q[i]=="Sunday.")day[jj][l[jj]++]=7; } } for (int i=1;i<=m;i++) for (int j=1;j<=7;j++) { int fa=0,T,F,abc=0; for (int k=1;k<=m;k++) { T=F=0; for (int kk=0;kk<l[k];kk++) { if (s[k][kk]==1) { if (i==k)T=1;else F=1; } if (s[k][kk]==2) { if (i!=k)T=1;else F=1; } if (s[k][kk]==3) { if (i==d[k][kk])T=1;else F=1; } if (s[k][kk]==4) { if (i!=d[k][kk])T=1;else F=1; } if (s[k][kk]==5) { if (j==day[k][kk])T=1;else F=1; } } if (T && F)break; if (F)fa++; if (!T && !F)abc++; } if (T && F)continue; if (fa==n || fa<=n && fa+abc>=n)gu[i]=1; } int ans=0; for (int i=1;i<=m;i++) if (gu[i])ans++; if (!ans)printf("Impossible"); else if (ans>1)printf("Cannot Determine"); else for (int i=1;i<=m;i++)if (gu[i]){cout<<h[i];break;} return 0; }
(这不是我的code我的还没调试完 会补上的
T3 加分二叉树
题目描述
设一个n个节点的二叉树tree的中序遍历为(1,2,3,…,n),其中数字1,2,3,…,n为节点编号。每个节点都有一个分数(均为正整数),记第i个节点的分数为di,tree及它的每个子树都有一个加分,任一棵子树subtree(也包含tree本身)的加分计算方法如下:
subtree的左子树的加分× subtree的右子树的加分+subtree的根的分数。
若某个子树为空,规定其加分为1,叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。要求输出;
(1)tree的最高加分
(2)tree的前序遍历
输入输出格式
输入格式:
第1行:一个整数n(n<30),为节点个数。
第2行:n个用空格隔开的整数,为每个节点的分数(分数<100)。
输出格式:
第1行:一个整数,为最高加分(结果不会超过4,000,000,000)。
第2行:n个用空格隔开的整数,为该树的前序遍历。
输入输出样例
5 5 7 1 2 10
145 3 1 2 4 5
题解
这个题可以用动态规划或者记忆化搜索来做。因为如果要求加分最大的话,必须要求它的儿子结点
加分最大,所以就有了最优子阶段。我们可以枚举根来更新最大值。中序遍历有个特点,在中序遍
历这个序列上,某个点左边的序列一定是这个点的左子树,右边的序列,一定在这个点的右子树。
root[i,j]表示[i,j]这段序列的根,递归输出先序遍历。注意初始化,f[i][i]=v[i],当序列只有I一个元素时,f[i][i]等于这个点本身
的权值,当l==r-1时,此时是空树设为1。
啦啦啦啦代码来啦 两种方法
code
动态规划 区间dp
#include<iostream> #include<cstdio> using namespace std; int n,v[39],f[47][47],i,j,k,root[49][49]; void print(int l,int r){ if(l>r)return; if(l==r){printf("%d ",l);return;} printf("%d ",root[l][r]); print(l,root[l][r]-1); print(root[l][r]+1,r); } int main() { scanf("%d",&n); for( i=1; i<=n; i++) scanf("%d",&v[i]); for(i=1; i<=n; i++) {f[i][i]=v[i];f[i][i-1]=1;} for(i=n; i>=1; i--) for(j=i+1; j<=n; j++) for(k=i; k<=j; k++) { if(f[i][j]<(f[i][k-1]*f[k+1][j]+f[k][k])) { f[i][j]=f[i][k-1]*f[k+1][j]+f[k][k]; root[i][j]=k; } } printf("%d ",f[1][n]); print(1,n); return 0; }
记忆化搜索
#include<iostream> #include<cstdio> using namespace std; int n,v[49],dp[49][49],root[49][49]; int ser(int l,int r){ if(dp[l][r]>0)return dp[l][r]; if(l==r)return v[l]; if(r<l)return 1; for(int i=l;i<=r;i++){ int p=ser(l,i-1)*ser(i+1,r)+dp[i][i]; if(p>dp[l][r]){ dp[l][r]=p;root[l][r]=i; } } return dp[l][r]; } void print(int l,int r){ if(r<l)return; if(l==r){printf("%d ",l);return;} printf("%d ",root[l][r]); print(l,root[l][r]-1); print(root[l][r]+1,r); } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d",&v[i]),dp[i][i]=v[i]; printf("%d ",ser(1,n)); print(1,n); return 0; }
T4传染病控制
题目背景
近来,一种新的传染病肆虐全球。蓬莱国也发现了零星感染者,为防止该病在蓬莱国大范围流行,该国政府决定不惜一切代价控制传染病的蔓延。不幸的是,由于人们尚未完全认识这种传染病,难以准确判别病毒携带者,更没有研制出疫苗以保护易感人群。于是,蓬莱国的疾病控制中心决定采取切断传播途径的方法控制疾病传播。经过 WHO(世界卫生组织)以及全球各国科研部门的努力,这种新兴传染病的传播途径和控制方法已经研究清楚,剩下的任务就是由你协助蓬莱国疾控中心制定一个有效的控制办法。
题目描述
研究表明,这种传染病的传播具有两种很特殊的性质;
第一是它的传播途径是树型的,一个人X只可能被某个特定的人Y感染,只要Y不得病,或者是XY之间的传播途径被切断,则X就不会得病。
第二是,这种疾病的传播有周期性,在一个疾病传播周期之内,传染病将只会感染一代患者,而不会再传播给下一代。
这些性质大大减轻了蓬莱国疾病防控的压力,并且他们已经得到了国内部分易感人群的潜在传播途径图(一棵树)。但是,麻烦还没有结束。由于蓬莱国疾控中心人手不够,同时也缺乏强大的技术,以致他们在一个疾病传播周期内,只能设法切断一条传播途径,而没有被控制的传播途径就会引起更多的易感人群被感染(也就是与当前已经被感染的人有传播途径相连,且连接途径没有被切断的人群)。当不可能有健康人被感染时,疾病就中止传播。所以,蓬莱国疾控中心要制定出一个切断传播途径的顺序,以使尽量少的人被感染。
你的程序要针对给定的树,找出合适的切断顺序。
输入输出格式
输入格式:
输入格式的第一行是两个整数n(1≤n≤300)和p。接下来p行,每一行有两个整数i和j,表示节点i和j间有边相连(意即,第i人和第j人之间有传播途径相连)。其中节点1是已经被感染的患者。
输出格式:
只有一行,输出总共被感染的人数。
输入输出样例
7 6 1 2 1 3 2 4 2 5 3 6 3 7
3
题解 枚举+搜索
贪心了半天 每次切掉重儿子竟然是错了 详情画菊花图自行脑补
贪心90
#include<iostream> #include<cstdio> #include<queue> #include<algorithm> using namespace std; queue<int>q,qq; int n,p,x,y,ans=1,sumedge; int head[321],siz[321]; struct Edge{ int x,y,nxt; Edge(int x=0,int y=0,int nxt=0): x(x),y(y),nxt(nxt){} }edge[321]; void add(int x,int y){ edge[++sumedge]=Edge(x,y,head[x]); head[x]=sumedge; } void dfs(int x){ siz[x]=1; for(int i=head[x];i;i=edge[i].nxt){ int v=edge[i].y; dfs(v); siz[x]+=siz[v]; } } void slove(){ int u=0; if(q.size()==0)return; while(q.size()){ int now=q.front();q.pop();qq.push(now); for(int i=head[now];i;i=edge[i].nxt){ int v=edge[i].y; if(siz[v]>siz[u])u=v; } } while(qq.size()){ int now=qq.front();qq.pop(); for(int i=head[now];i;i=edge[i].nxt){ int v=edge[i].y; if(v!=u){ q.push(v);ans++; // cout<<v<<endl; } } } slove(); } int main(){ //freopen("epidemic.in","r",stdin); // freopen("epidemic.out","w",stdout); scanf("%d%d",&n,&p); for(int i=1;i<=p;i++){ scanf("%d%d",&x,&y); if(x>y)swap(x,y); add(x,y); } dfs(1);q.push(1); slove(); printf("%d ",ans); return 0; }
AC
#include<iostream> #include<cmath> #include<cstdio> #define mx 313 using namespace std; int n,p,x,y,sumedge,ans=2147483645,flag,cut[mx],head[mx],dep[mx],fa[mx],deep[mx][mx]; struct Edge{ int x,y,nxt; Edge(int x=0,int y=0,int nxt=0): x(x),y(y),nxt(nxt){} }edge[mx]; void add(int x,int y){ edge[++sumedge]=Edge(x,y,head[x]); head[x]=sumedge; } void dfs1(int x){ dep[x]=dep[fa[x]]+1;deep[dep[x]][++deep[dep[x]][0]]=x; for(int i=head[x];i;i=edge[i].nxt){ int v=edge[i].y;fa[v]=x; dfs1(v); } } void dfs2(int x,int sum){ if(sum>=ans)return;flag=0; for(int i=1;i<=deep[x][0];i++){ int v=deep[x][i]; if(cut[fa[v]]==0){flag=1;sum++;cut[v]=0;} } if(flag)sum--; for(int i=1;i<=deep[x][0];i++){ int v=deep[x][i]; if(cut[v])continue; cut[v]=1; dfs2(x+1,sum); cut[v]=0; } for(int i=1;i<=deep[x][0];i++){ int v=deep[x][i]; cut[v]=1; } if(flag==0)ans=min(ans,sum); } int main(){ scanf("%d%d",&n,&p); for(int i=1;i<=p;i++){ scanf("%d%d",&x,&y); if(x>y)swap(x,y); add(x,y); } for(int i=1;i<=n;i++)cut[i]=1;cut[1]=0; dfs1(1);dfs2(2,1); printf("%d ",ans); return 0; }