

题解:
贪心+dp
30% N<=5 5!枚举一下
20% 高度没有的时候,高度花费就不存在了,将ci排序,
从小到大挨个跳。另外,20% 准备跳楼没有花费,那么跳
楼的高度一定是从小到大,或者是从大到小。所以按照hi从
小到大排序,那么跳楼一定是排序后连续的一段。枚举第一
栋楼从哪开始跳。对于100% (1)hi从小到大排序,最后高度
的花费一定是hend-hstart。那么start—end中间楼的高度就
不会造成影响,只需要将start—end中间的楼排序,取小的ci。
(2)现在跳在第i栋楼上,已经跳了j栋楼了的最小花费。
f[i][j]—>min{ f[k][j+1]+c[k]+abs{h[i]-h[k]} }
最后答案是枚举i,j。
代码:
暴力挂了20

#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #define maxn 60 using namespace std; int n,t,ans,flag1,flag2,flag3; int vis[maxn]; struct Build{ int h,c; }b[maxn]; inline int read(){ int x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1; for(;isdigit(ch);ch=getchar())x=x*10+ch-'0'; return x*f; } bool cmp1(Build a,Build b){ return a.c<b.c; } bool cmp2(Build a,Build b){ return a.h<b.h; } void dfs(int nxt,int now,int sum){ sum+=b[now].c; if(sum>t)return; ans=max(ans,nxt-1); for(int i=1;i<=n;i++){ if(vis[i]==0){ vis[i]=1; if(nxt==1){ dfs(nxt+1,i,sum); vis[i]=0; }else { dfs(nxt+1,i,sum+abs(b[now].h-b[i].h)); vis[i]=0; } } } return; } int main(){ freopen("meet.in","r",stdin); freopen("meet.out","w",stdout); n=read();flag1=true;flag2=true; for(int i=1;i<=n;i++)b[i].c=read(); for(int i=1;i<=n;i++)b[i].h=read(); t=read(); if(n<=5){ dfs(1,0,0); printf("%d ",ans); fclose(stdin);fclose(stdout); return 0; } for(int i=2;i<=n;i++){ if(b[i].h!=b[i-1].h){ flag1=false;break; } } if(flag1){ int ret=0; sort(b+1,b+n+1,cmp1); for(int i=1;i<=n;i++){ if(t-b[i].c>0){ ret++;t-=b[i].c; } } printf("%d ",ret); fclose(stdin);fclose(stdout); return 0; } for(int i=1;i<=n;i++){ if(b[i].c){ flag2=false;break; } } if(flag2){ sort(b+1,b+n+1,cmp2); for(int len=1;len<=n;len++){ flag3=false; for(int st=1;st+len-1<=n;st++){ int ed=st+len-1,pre=b[st].h,f=0; for(int i=st;i<=ed;i++){ f+=b[i].h-pre; pre=b[i].h; } if(f<=t)flag3=true,ans=max(ans,len); } if(flag3==false)break; } printf("%d ",ans); fclose(stdin);fclose(stdout); return 0; } dfs(1,0,0); printf("%d ",ans); fclose(stdin);fclose(stdout); return 0; }
正解

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; int n,t,ans; int f[55][55]; struct Build{ int c,h; bool operator < (const Build &a) const{ h<a.h; } }a[55]; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d",&a[i].c); for(int i=1;i<=n;i++)scanf("%d",&a[i].h); scanf("%d",&t); sort(a+1,a+n+1); memset(f,0x3f,sizeof(f)); for(int i=0;i<=n;i++)f[i][1]=a[i].c; for(int i=1;i<=n;i++) for(int j=1;j<=i;j++){ for(int k=1;k<i;k++) f[i][j]=min(f[i][j],f[k][j-1]+(j==1?0:a[i].h-a[k].h)+a[i].c); } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(f[i][j]<=t)ans=max(ans,j); printf("%d ",ans); return 0; }



题解:
假设
a1<a2<a3.....<an
b1<b2<b3...<b(n*(n-1)/2)
那么b1=a1+a2,b2=a1+a3....
a2+a3=bx,然后枚举bx,
根据
a1+a2=b1
a1+a3=b2
a2+a3=bx,
三个方程三个未知数,在b数组中删去b1,b2,bx,
那么b数组中剩下最小的一定是
a1+a4,a2+a4,a3+a4....都知道了,然后从b数组中删去。
重复上步。
代码还明白。

v#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int maxn=310; int n,m,res[maxn],ans[maxn][maxn],z[maxn*maxn],cnt; bool use[maxn*maxn]; void check(int p) { memset(use,false,sizeof(use)); if ((z[1]+z[2]+z[p])&1) return; res[1]=(z[1]+z[2]+z[p])/2-z[p]; res[2]=z[1]-res[1]; res[3]=z[2]-res[1]; use[1]=use[2]=use[p]=true; for (int a=4,b=3;a<=n;a++) { while (b<=m && use[b]) b++; if (b>m) return; res[a]=z[b]-res[1]; use[b]=true; for (int c=2;c<a;c++) { if (res[c]>res[a]) return; int v=res[c]+res[a]; int p=lower_bound(z+1,z+m+1,v)-z; if (z[p]!=v) return; int px=p; while (px && z[px]==z[p]) px--; px++; while (px<=m && z[px]==z[p] && use[px]) px++; if (z[px]!=z[p] || use[px]) return; p=px; use[p]=true; } } cnt++; for (int a=1;a<=n;a++) ans[cnt][a]=res[a]; } int main() { freopen("city.in","r",stdin); freopen("city.out","w",stdout); scanf("%d",&n); m=n*(n-1)/2; for (int a=1;a<=m;a++) scanf("%d",&z[a]); sort(z+1,z+m+1); for (int a=3;a<=m;) { check(a); int b=a; while (b<=m && z[b]==z[a]) b++; a=b; } printf("%d ",cnt); for (int a=1;a<=cnt;a++) for (int b=1;b<=n;b++) { printf("%d",ans[a][b]); if (b==n) printf(" "); else printf(" "); } return 0; }


题解:
又写挂的暴力.

#include<iostream> #include<cstdio> #include<cstring> #define maxn 100009 #define maxm 70009 using namespace std; int n,m,gg,cnt,ans,pp; int a[maxn],sum[10008][500],p[10008]; struct Q{ int l,r,v,id; }q[maxn]; inline int read(){ int x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1; for(;isdigit(ch);ch=getchar())x=x*10+ch-'0'; return x*f; } void slove1(){ for(int i=1;i<=n;i++)a[i]=read(); for(int i=1;i<=m;i++){ int l,r,p,v,ans=0; l=read();r=read();p=read();v=read(); for(int j=l;j<=r;j++) if(a[j]%p==v)ans++; printf("%d ",ans); } } void slove2(){ for(int i=1;i<=n;i++)a[i]=read(); for(int i=1;i<=m;i++){ q[i].l=read();q[i].r=read();pp=read();q[i].v=read(); } for(int i=1;i<=n;i++){ a[i]%=pp;if(!p[a[i]])p[a[i]]=++cnt; } for(int i=1;i<=n;i++){ for(int j=1;j<=cnt;j++)sum[i][j]=sum[i-1][j]; sum[i][p[a[i]]]++; } for(int i=1;i<=m;i++){ int L=q[i].l,R=q[i].r,V=q[i].v; printf("%d ",sum[R][p[V]]-sum[L-1][p[V]]); } } int main(){ freopen("light.in","r",stdin); freopen("light.out","w",stdout); n=read();m=read(); if(n<=1000&&m<=1000){ slove1(); fclose(stdin);fclose(stdout); return 0; }else slove2(); fclose(stdin);fclose(stdout); return 0; }
正解:下面是自己都mengbi的笔记
暴力30%
P相同的30%,将ai%p的值存在vector里。
每次询问时寻找vector,用个数据结构维护一下。
1 5 2 3 4 q=3
1 2 2 0 1
V=0 4
V=1 1 5
V=2 2 3
二分找。空间大小是O(n),可以用vector去搞。
100%做法
对于每一个p需要处理每一个数%p之后在0—n-1的哪一个位置。
100%的数据和之前的区别是p不一样了是吧。只考虑p<=10^4。
可以对每一个p做一个预处理,然后建一个0—n-1的数组,每个p有个O(n)的
空间,那么有O(np),会TLE。所以不能对所有的p进行处理。那么对哪些p进
行处理呢?可以对1<=p<=100,进行处理。对于1<=p<=100,套用60%的做法,
像之前预处理,空间100*n,询问去数组里二分找就可以了。P>100怎么做呢?
我们不可能对那么多p进行处理,考虑每个询问,l-r,能被统计进答案的数是哪些?
是v,v+p,v+2p…..V+KP<=10^4,p>100,那么k<100,说明不到100个数。求p+kv
在l—r中出现了多少次????在数组里二分求。就是把60%的模p改成不模p。
代码:

#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int maxn=310; int n,m,res[maxn],ans[maxn][maxn],z[maxn*maxn],cnt; bool use[maxn*maxn]; void check(int p) { memset(use,false,sizeof(use)); if ((z[1]+z[2]+z[p])&1) return; res[1]=(z[1]+z[2]+z[p])/2-z[p]; res[2]=z[1]-res[1]; res[3]=z[2]-res[1]; use[1]=use[2]=use[p]=true; for (int a=4,b=3;a<=n;a++) { while (b<=m && use[b]) b++; if (b>m) return; res[a]=z[b]-res[1]; use[b]=true; for (int c=2;c<a;c++) { if (res[c]>res[a]) return; int v=res[c]+res[a]; int p=lower_bound(z+1,z+m+1,v)-z; if (z[p]!=v) return; int px=p; while (px && z[px]==z[p]) px--; px++; while (px<=m && z[px]==z[p] && use[px]) px++; if (z[px]!=z[p] || use[px]) return; p=px; use[p]=true; } } cnt++; for (int a=1;a<=n;a++) ans[cnt][a]=res[a]; } int main() { freopen("city.in","r",stdin); freopen("city.out","w",stdout); scanf("%d",&n); m=n*(n-1)/2; for (int a=1;a<=m;a++) scanf("%d",&z[a]); sort(z+1,z+m+1); for (int a=3;a<=m;) { check(a); int b=a; while (b<=m && z[b]==z[a]) b++; a=b; } printf("%d ",cnt); for (int a=1;a<=cnt;a++) for (int b=1;b<=n;b++) { printf("%d",ans[a][b]); if (b==n) printf(" "); else printf(" "); } return 0; }


题解:贪心
遇到右括号和待匹配的左括号匹配。没有待匹配的左括号那么
将这个右括号改成左括号。最后将剩余的左括号一半改成右括
号进行匹配。
代码:

#include<iostream> #include<cstdio> #include<cstring> #define maxn 100009 using namespace std; char s[maxn]; int len,top,ans; int main(){ freopen("shower.in","r",stdin); freopen("shower.out","w",stdout); scanf("%s",s+1);len=strlen(s+1); for(int i=1;i<=len;i++){ if(s[i]=='(')top++; else { if(top)top--; else ans++,top++; } } printf("%d ",ans+top/2); fclose(stdin);fclose(stdout); return 0; }


题解:线性筛+前缀和+二分
那么求连续k个质数的和就是O(1)的了。
发现,在前面选k个比在后面选k个小,这说明是有单调性的,二分k个
数最后一个数的位置。也可以二分第一个数。
代码:

#include<iostream> #include<cstdio> #include<cstring> #define maxn 1000009 #define LL long long using namespace std; LL n; int t,k,cnt; int check[maxn],prime[maxn]; LL sum[maxn]; inline LL read(){ LL x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1; for(;isdigit(ch);ch=getchar())x=x*10+ch-'0'; return x*f; } void Prime(){ check[1]=true; for(int i=2;i<=1000000;i++){ if(!check[i])prime[++cnt]=i,sum[cnt]=sum[cnt-1]+i; for(int j=1;j<=cnt&&i*prime[j]<=1000000;j++){ check[i*prime[j]]=true; if(i%prime[j]==0)break; } } } int main(){ freopen("diary.in","r",stdin); freopen("diary.out","w",stdout); scanf("%d",&t); Prime(); for(int i=1;i<=t;i++){ n=read();scanf("%d",&k); int l=1,r=cnt; LL ans=0; while(l<=r){ int mid=(l+r)>>1; int p=mid-k; if(p>=0){ LL gg=sum[mid]-sum[p]; if(gg<=n){ ans=gg; l=mid+1; }else r=mid-1; }else l=mid+1; } if(ans==0)printf("-1 "); else printf("%I64d ",ans); } fclose(stdin);fclose(stdout); return 0; }



题解:
30%暴力建树+floyed

#include<iostream> #include<cstdio> #include<cstring> #define LL long long #define mod 1000000007 using namespace std; int m,a,b,c,d,l; int tree[30][300][300],node[30]; void make_tree(int k){ LL ans=0; int num=node[a];node[k]=node[a]+node[b]; for(int i=1;i<=node[a];i++) for(int j=1;j<=node[a];j++) tree[k][i][j]=tree[a][i][j]; for(int i=1;i<=node[b];i++) for(int j=1;j<=node[b];j++) tree[k][i+num][j+num]=tree[b][i][j]; tree[k][c][num+d]=tree[k][num+d][c]=l; for(int kk=1;kk<=node[k];kk++) for(int i=1;i<=node[k];i++) for(int j=1;j<=node[k];j++) tree[k][i][j]=min(tree[k][i][j],tree[k][i][kk]+tree[k][kk][j]); for(int i=1;i<=node[k];i++) for(int j=i+1;j<=node[k];j++) ans=(ans%mod+tree[k][i][j]%mod)%mod; printf("%I64d ",ans); } int main(){ freopen("cloth.in","r",stdin); freopen("cloth.out","w",stdout); scanf("%d",&m);node[0]=1; memset(tree,0x3f,sizeof(tree)); for(int i=1;i<=28;i++) for(int j=1;j<=280;j++) tree[i][j][j]=0; for(int i=1;i<=m;i++){ scanf("%d%d%d%d%d",&a,&b,&c,&d,&l); c++;d++; make_tree(i); } fclose(stdin);fclose(stdout); return 0; }
60%是让你线性树形dp的
下面是我记的笔记..具体在写什么我也mengbi了。
发现是由左边的树和右边的树拼起来的,那么答案肯定有左边和右边的答案。
F(TI)=F(TJ)+F(TK)+?
肯定包括左边内部距离和右边内部距离。
?就是左边的点到右边的点的距离。
具体考虑怎样算这一部分。
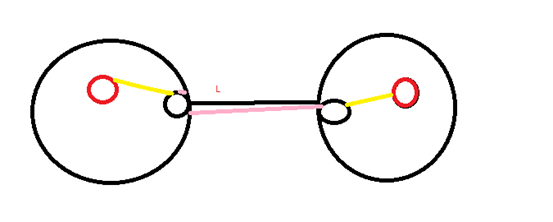
看L会走size[j]*size[k]*L
G[j][p1]第j棵树所有点到p1的距离之和。
Size[j]*G[k][p2]+size[j]*size[k]*l+size[k]*G[j][1]
Size[]在合并的时候就可以求出Size的大小。
关键是G[j][p]怎么求?可以分成两部分来求。
第I棵树中所有点到p的距离,是第j棵树到p的距离和第k
树到p的距离的和。那么第K棵树到所有点的距离到底怎么算。
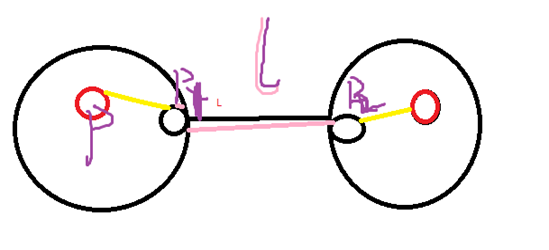
首先右边某点到左边,l和dis[p1][p]是不变的。
(l+dis[i][p][p1])第i棵树p到p1的距离。
G[i][p]的第二维有2^m种可能。算不了..空间大…会炸….
记忆化搜索,没必要求出所有的,把连起来的那两个算出来就可以了。
代码:

#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> #include<map> using namespace std; const int mo=1000000007; const int maxn=100; int n,id1[maxn],id2[maxn],l[maxn],res[maxn]; long long num1[maxn],num2[maxn],size[maxn]; struct rec { int p; long long p1,p2; rec(){} rec(int a,long long b,long long c) { p=a; if (b<c) p1=b,p2=c; else p1=c,p2=b; } bool operator<(const rec &a)const { if (p!=a.p) return p<a.p; if (p1!=a.p1) return p1<a.p1; return p2<a.p2; } }; map< pair<int,long long > ,int > ma; map<rec,int> ma2; int solve(int p,long long p1,long long p2) { if (!p) return 0; if (p1==p2) return 0; rec x=rec(p,p1,p2); if (ma2.count(x)) return ma2[x]; if (p1<size[id1[p]]) { if (p2<size[id1[p]]) ma2[x]=solve(id1[p],p1,p2); else ma2[x]=((long long)solve(id1[p],num1[p],p1)+solve(id2[p],num2[p],p2-size[id1[p]])+l[p])%mo; } else { if (p2<size[id1[p]]) ma2[x]=((long long)solve(id1[p],num1[p],p2)+solve(id2[p],num2[p],p1-size[id1[p]])+l[p])%mo; else ma2[x]=solve(id2[p],p1-size[id1[p]],p2-size[id1[p]]); } return ma2[x]; } int solve(int p,long long n) { if (p==0) return 0; pair<int,long long> px; px=make_pair(p,n); if (ma.count(make_pair(p,n))) return ma[px]; if (n<size[id1[p]]) ma[px]=(((long long)solve(id1[p],num1[p],n)+l[p])*(size[id2[p]]%mo)%mo+solve(id2[p],num2[p])+solve(id1[p],n))%mo; else ma[px]=(((long long)solve(id2[p],num2[p],n-size[id1[p]])+l[p])*(size[id1[p]]%mo)%mo+solve(id1[p],num1[p])+solve(id2[p],n-size[id1[p]]))%mo; return ma[px]; } int main() { freopen("cloth.in","r",stdin); freopen("cloth.out","w",stdout); while (~scanf("%d",&n)) { ma.clear(); ma2.clear(); for (int a=1;a<=n;a++) scanf("%d%d%I64d%I64d%d",&id1[a],&id2[a],&num1[a],&num2[a],&l[a]); size[0]=1; for (int a=1;a<=n;a++) size[a]=size[id1[a]]+size[id2[a]]; for (int a=1;a<=n;a++) res[a]=((long long)solve(id1[a],num1[a])*(size[id2[a]]%mo)%mo+(long long)(size[id1[a]]%mo)*(size[id2[a]]%mo)%mo*l[a]%mo+(long long)solve(id2[a],num2[a])*(size[id1[a]]%mo)%mo+res[id1[a]]+res[id2[a]])%mo; for (int a=1;a<=n;a++) printf("%d ",res[a]); } return 0; }
小结:
上午 :
预计分数:70+0+60
实际得分:50+0+30
下午:
预计分数:100+100+30
实际得分:100+100+40
反思:
上午一直想最后一题后30%的暴力,前缀和
能MLE,侥幸尽量开大数组....结果一分没有....
再也不写玄学暴力了....
下午还好...题有点水...
T1做过秒过...T2想了想就秒了...
T3...一脸bengbi...暴力都不会写...怎么存图什么的...
想了半天...硬着头皮写还是很好写的....
早上吃多了一天都撑的难受..【哭唧唧QAQ
