Algorithms

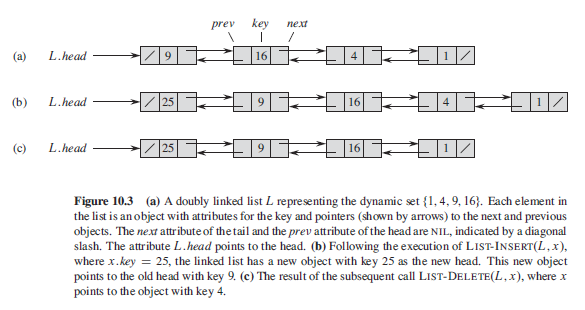
相关概念
    linkedlist链表是中这样的数据结构：其中的各个对象按线性顺序排列.数组的线性顺序是由数组的下标决定.
    与数组不同的地方是linkedlist的顺序是由各个对象的指针决定的。
    linkedlist为动态集合提供了一种简单而灵活的表示方法。
    
    doublylinkedlist双向链表的每个元素都是一个对象,每个对象有一个关键字Key和两个指针：next和prev.
    对象中还可以包括其他的辅助数据或称为卫星数据.
    若x为链表的一个元素.x.next指向它在链表中的'后继'元素,x.prev则指向它的'前驱'元素.
    如果x.prev=NIL,则没有前驱,是链表的第一个元素,即链表的头head.
    如果x.next=NIL,则没有后继,是链表的最后一个元素,即链表的尾tail.
    
    linkedlist可以有多种形式.它可以是单链接的或双链接的.可以是已排序的或未排序的.
    可以是循环的或非循环的.如果一个链表是单链接的singlelinked,则省略每个元素中的prev指针.
    如果链表是已排序的sorted,则链表的线性顺序与链表元素中的关键字的线性顺序一致.最小元素在head,最大元素在tail.
    在循环链表中circularlist中,表头的元素的prev指针指向表尾元素,儿表尾元素的nex指针指.
 

    linked list 的搜索
        list_search 采用简单的线性搜索方法, 用于查找链表 L 中的第一个关键字为 k 的元素, 并反馈指向该元素的指针.
        如果链表 L 里面没有关键字为 k 的对象, 则反回 NIL.

Python Programming

class linked_list(list):
    def __init__(self):
        self.cursor = -1
        #self.depth = depth
        #if len(self) != 0:
        self.head = 'NIL'             #  'NIL' 起到哨兵 sentinel 的作用, 用来简化边界条件处理.
        self.tail = 'NIL'             #  sentinel 不能降低数据结构相关操作的渐近时间, 但可以降低常数因子
                                       #  在循环语句中使用哨兵 sentinel 的好处往往在于可以使代码简洁, 而非提高速度. 

    def __new__(cls, **kwargs):
        obj = super(linked_list, cls).__new__(cls)
        #while depth:
        #obj.append('NIL')
            #depth -= 1
        return obj

    def prev(self):
        if self.cursor == 0:
            return 'NIL'
        else:
            self.cursor -= 1
            return self[self.cursor]

    def next(self):
        if self.cursor +1 == len(self):
            return 'NIL'
        else:
            self.cursor += 1
            return self[self.cursor]

    def update_head_tail(self):
        if len(self) == 0:
            self.head = 'NIL'
            self.tail = 'NIL'
        else:
            self.head = self[0]
            self.tail = self[-1]

def list_search(L, k):
    x = L.head
    while x != 'NIL' and x != k:
        x = L.next()
    if x == 'NIL':
        return 'Not found the element : %s ' % str(k)
    else:
        return L.index(x)

def list_insert(L, x):
    L.insert(0, x)
    L.cursor += 1
    L.update_head_tail()

def list_delete(L, x):
    search = list_search(L, x)
    if 'Not found' in str(search):
        return 'Cannot delete ! the element is not found : %s' % x
    else:
        print('Deleting ', L, search)
        L.pop(search)
        L.cursor -= 1
        L.update_head_tail()

 
if __name__ == '__main__':

    ll = linked_list()
    print('Searching 0')
    print(list_search(ll, 0))
    print(ll, ll.cursor)

    print('Inserting 3')
    list_insert(ll, 3)
    print(ll, ll.cursor, ll.head)

    print('Searching 3')
    print(list_search(ll, 3))

    print('Operating deletion of 5')
    print(list_delete(ll, 5))
    print(ll, ll.cursor, ll.head)

    print('Operating deletion of 3')
    list_delete(ll, 3)
    print(ll, ll.cursor, ll.head)


结果打印:
Searching 0
Not found the element : 0 
[] -1
Inserting 3
[3] 0 3
Searching 3
0
Operating deletion of 5
Cannot delete ! the element is not found : 5
[3] 0 3
Operating deletion of 3
Deleting  [3] 0
[] -1 NIL

Reference

    1. Introduction to algorithms