IIR Filter Design
One of the drawbacks of FIR filters is that they require a large filter order to meet some design specifications. If the ripples are kept constant, the filter order grows inversely proportional to the transition width. By using feedback, it is possible to meet a set of design specifications with a far smaller filter order. This is the idea behind IIR filter design. The term "infinite impulse response" (IIR) stems from the fact that, when an impulse is applied to the filter, the output never decays to zero.
-
IIR filters are useful when computational resources are at a premium. However, stable, causal IIR filters cannot have perfectly linear phase. Avoid IIR designs in cases where phase linearity is a requirement.
Another important reason for using IIR filters is their small group delay relative to FIR filters, which results in a shorter transient response.
Butterworth Filters
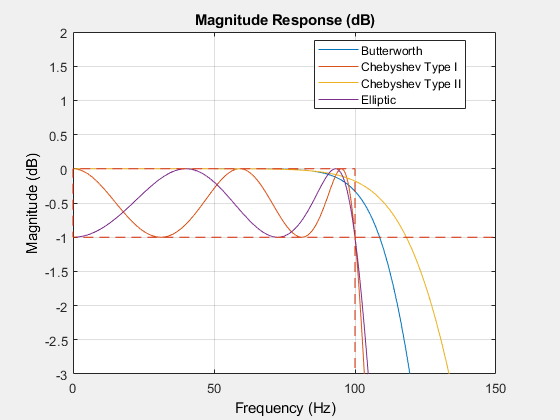
Design a minimum-order Butterworth filter with passband frequency 100 Hz, stopband frequency 300 Hz, maximum passband ripple 1 dB, and 60 dB stopband attenuation. The sample rate is 2 kHz.
Fp = 100;
Fst = 300;
Ap = 1;
Ast = 60;
Fs = 2e3;
dbutter = designfilt('lowpassiir','PassbandFrequency',Fp,'StopbandFrequency',Fst,
'PassbandRipple',Ap,'StopbandAttenuation',Ast,'SampleRate',Fs,'DesignMethod','butter');
Chebyshev Type I Filters
Chebyshev Type I filters attain smaller transition widths than Butterworth filters of the same order by allowing for passband ripple.
-
Butterworth and Chebyshev Type I filters both have maximally flat stopbands. For a given filter order, the tradeoff is between passband ripple and transition width.
Design a Chebyshev Type I filter with the same specifications as the Butterworth filter above.
dcheby1 = designfilt('lowpassiir','PassbandFrequency',Fp,'StopbandFrequency',Fst,
'PassbandRipple',Ap,'StopbandAttenuation',Ast,'SampleRate',Fs,'DesignMethod','cheby1');
Chebyshev Type II Filters
-
Chebyshev Type II filters have maximally flat passbands and equiripple stopbands.
Since extremely large attenuations are typically not required, we may be able to attain the required transition width with a relatively small order by allowing for some stopband ripple.
Design a minimum-order Chebyshev Type II filter with the same specifications as in the previous examples.
dcheby2 = designfilt('lowpassiir','PassbandFrequency',Fp,'StopbandFrequency',Fst,
'PassbandRipple',Ap,'StopbandAttenuation',Ast,'SampleRate',Fs,'DesignMethod','cheby2');
Elliptic Filters
Elliptic filters generalize Chebyshev and Butterworth filters by allowing for ripple in both the passband and the stopband. As ripples are made smaller, elliptic filters can approximate arbitrarily close the magnitude and phase response of either Chebyshev or Butterworth filters.
-
Elliptic filters attain a given transition width with the smallest order.
dellip = designfilt('lowpassiir','PassbandFrequency',Fp,'StopbandFrequency',Fst,
'PassbandRipple',Ap,'StopbandAttenuation',Ast,'SampleRate',Fs,'DesignMethod','ellip');
Compare the response and the order of the four IIR filters.
-
For the same specification constraints, the Butterworth method yields the highest order and the elliptic method yields the smallest.
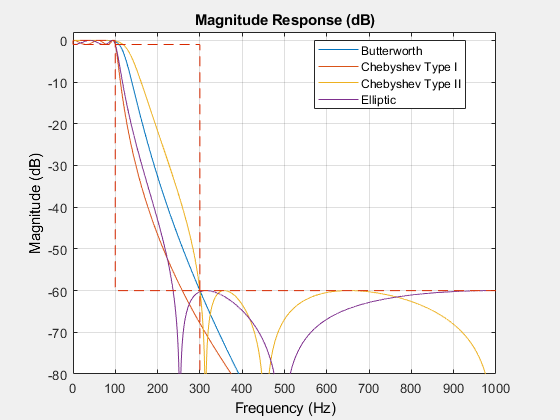
Zoom into the passband to see the ripple differences.