DSP

The discrete Fourier transform, or DFT, is the primary tool of digital signal processing. The foundation of the product is the fast Fourier transform (FFT), a method for computing the DFT with reduced execution time. 

For the input sequence x and its transformed version X (the discrete-time Fourier transform at equally spaced frequencies around the unit circle), the two functions implement the relationships

 

Note  The MATLAB convention is to use a negative j for the fft function. This is an engineering convention; physics and pure mathematics typically use a positive j.

fft, with a single input argument, x, computes the DFT of the input vector or matrix. If x is a vector, fft computes the DFT of the vector; if x is a rectangular array, fft computes the DFT of each array column.

For example, create a time vector and signal:

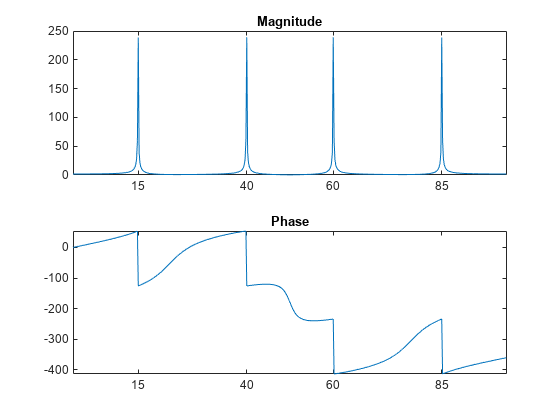
t = 0:1/100:10-1/100;                     % Time vector
x = sin(2*pi*15*t) + sin(2*pi*40*t);      % Signal

Compute the DFT of the signal and the magnitude and phase of the transformed sequence. Decrease round-off error when computing the phase by setting small-magnitude transform values to zero.

y = fft(x);                               % Compute DFT of x
m = abs(y);                               % Magnitude
y(m<1e-6) = 0;
p = unwrap(angle(y));                     % Phase

To plot the magnitude and phase in degrees, type the following commands:

f = (0:length(y)-1)*100/length(y);        % Frequency vector

subplot(2,1,1)
plot(f,m)
title('Magnitude')
ax = gca;
ax.XTick = [15 40 60 85];

subplot(2,1,2)
plot(f,p*180/pi)
title('Phase')
ax = gca;
ax.XTick = [15 40 60 85];

A second argument to fft specifies a number of points n for the transform, representing DFT length:

n = 512;
y = fft(x,n);
m = abs(y);
p = unwrap(angle(y));
f = (0:length(y)-1)*100/length(y);

subplot(2,1,1)
plot(f,m)
title('Magnitude')
ax = gca;
ax.XTick = [15 40 60 85];

subplot(2,1,2)
plot(f,p*180/pi)
title('Phase')
ax = gca;
ax.XTick = [15 40 60 85];

In this case, fft pads the input sequence with zeros if it is shorter than n, or truncates the sequence if it is longer than n. If n is not specified, it defaults to the length of the input sequence. Execution time for fft depends on the length, n, of the DFT it performs; 

Note  The resulting FFT amplitude is A*n/2, where A is the original amplitude and n is the number of FFT points. This is true only if the number of FFT points is greater than or equal to the number of data samples. If the number of FFT points is less, the FFT amplitude is lower than the original amplitude by the above amount.

The inverse discrete Fourier transform function ifft also accepts an input sequence and, optionally, the number of desired points for the transform. Try the example below; the original sequence x and the reconstructed sequence are identical (within rounding error).

t = 0:1/255:1;
x = sin(2*pi*120*t);
y = real(ifft(fft(x)));

figure
plot(t,x-y)

　　　　　　　　　　　　　　　　　　Round Error 

 

 Reference

　　1. MathWorks