CCS

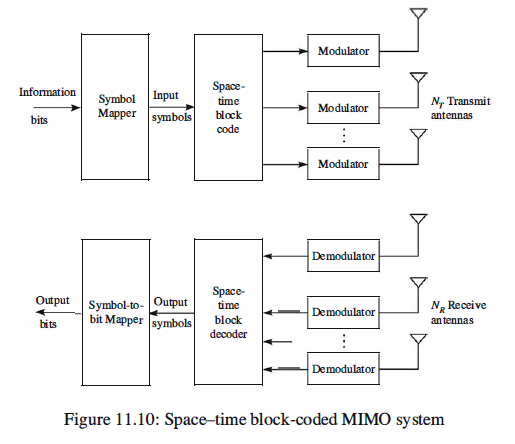
At the transmitter, the sequence of information bits is fed into a symbol mapper that maps a block of
bits into signal points {sd selected from a signal constellation such as PAM, PSK, or
QAM, consisting of M = 2^b signal points. These signal points are fed as a block to
a space-time encoder that maps the information symbols to a parallel set of identical
modulators. In turn, the modulators map the signal points into corresponding waveforms
that are transmitted simultaneously on the Nr antennas. Below, we describe two
types of space-time codes: block codes and trellis codes.

 Space-Time Block Codes

A space-time block code (STBC) is defined by a generator matrix G, having N rows
and Nr columns, of the form

 　　

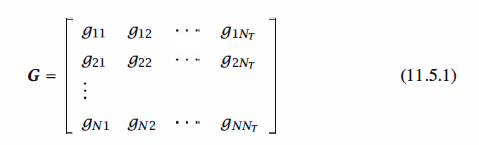
in which the elements {gij} are signal points resulting from a mapping of information
bits to corresponding signal points from a binary or M-ary signal constellation. By
employing Ny transmit antennas, each row of G may contain up to Ny different signal
points (symbols), which are transmitted on the Ny antennas in a time slot. Thus, the
first row of symbols in G is transmitted on the Ny antennas in the first time slot, the
second row of symbols in G is transmitted on the Ny antennas in the second time slot,
and the Nth row of symbols in G is transmitted on the Ny antennas in the Nth time slot.
Therefore, N time slots are used to transmit the symbols in the N rows of the generator
matrix G. The ratio of the number of different symbols transmitted to the number of
time slots is called the spatial code rate Rs  = Nt / N.

In the design of the generator matrix of a STBC, it is desirable to focus on three
principal objectives: (1) achieving the highest possible diversity of NyNR, (2) achieving
the highest possible (throughput) rate, and (3) minimizing the complexity of the
decoder.

Space-Time Block Codes(STBC)

 

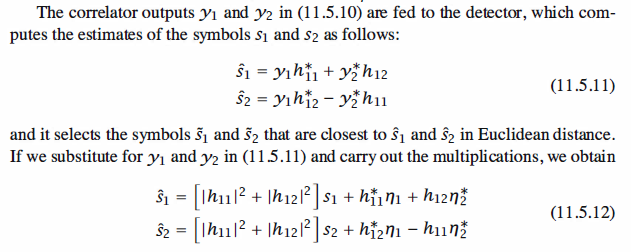
Matlab simulation code

% MATLAB script for STBC of MISO Nt=2 Nr=1 
echo on;
Nt = 2;                             % No. of transmit antennas
Nr = 1;                             % No. of receive antennas
codebook = [1+1i 1-1i -1+1i -1-1i]; % Reference codebook
Es = 2;                             % Energy per symbol
SNR_dB = 5:5:20;                    % SNR in dB
No = Es*10.^(-1*SNR_dB/10);         % Noise variance

% Preallocation for speed:
Dist1 = zeros(1,4);                 % Distance vector for s1
Dist2 = zeros(1,4);                 % Distance vector for s1
BER = zeros(1,length(SNR_dB));

% Maximum Likelihood Detector:
echo off;
for i = 1:length(SNR_dB)
    no_errors = 0;
    no_symbols = 0;
    while no_errors <= 100
        s = 2*randi([0 1],1,2)-1 + 1i*(2*randi([0 1],1,2)-1);
        no_symbols = no_symbols + 2;
        
        % Channel coefficients
        h = 1/sqrt(2) * (randn(1,2) + 1i*randn(1,2));

        % Noise generation:
        noise = sqrt(No(i))*(randn(2,1) + 1i*randn(2,1));

        % Correlator outputs:
        y(1) = h(1)*s(1) + h(2)*s(2) + noise(1);
        y(2) = -h(1)*conj(s(2)) + h(2)*conj(s(1)) + noise(2);

        % Estimates of the symbols s1 and s2:
        s_h(1) = y(1)*conj(h(1)) + conj(y(2))*h(2);
        s_h(2) = y(1)*conj(h(2)) - conj(y(2))*h(1);

        % Maximum-Likelihood detection:
        for j = 1 : 4
            Dist1(j) = abs(s_h(1)-codebook(j));
            Dist2(j) = abs(s_h(2)-codebook(j));
        end
        [Min1 idx1] = min(Dist1);
        [Min2 idx2] = min(Dist2);
        s_t(1) = codebook(idx1);
        s_t(2) = codebook(idx2);

        % Calculation of error numbers:
        if s_t(1) ~= s(1)
            no_errors = no_errors + 1;
        end
        if s_t(2) ~= s(2)
            no_errors = no_errors + 1;
        end
    end
    BER(i) = no_errors/no_symbols;
end
echo on;
semilogy(SNR_dB,BER)
xlabel('SNR (dB)')
ylabel('Symbol Error Rate (SER)')
legend('Alamouti: 4-PSK')


simulation result

Reference,

　　1. <<Contemporary Communication System using MATLAB>> - John G. Proakis