Multiamplitude Signal Transmission
In the preceding section, we treated the transmission of digital information by use of
binary signal waveforms. Thus, each signal waveform conveyed 1 bit of information.
In this section, we use signal waveforms that take on multiple amplitude levels. Thus,
we can transmit multiple bits per signal waveform.
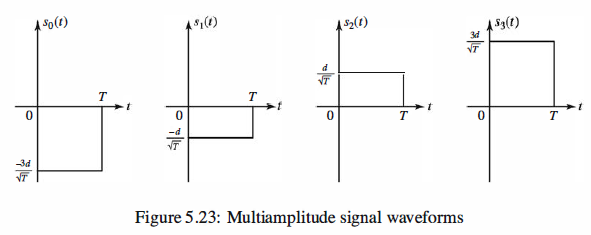
Signal Waveforms with Four Amplitude Levels


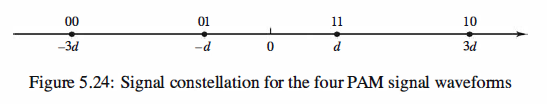
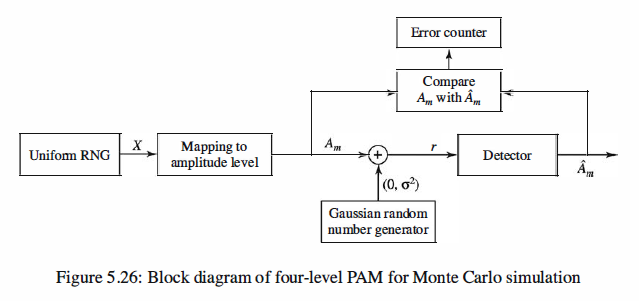
Optimum Receiver for the AWGN Channel
Signal Correlator
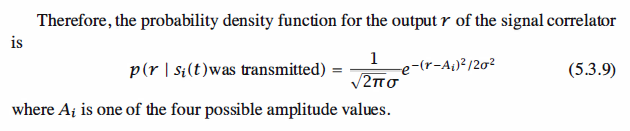
The Detector
The detector observes the correlator output r and decides which of the four PAM signals
was transmitted in the signal interval.
Because the received signal amplitude Ai can take the values ± d, ± 3d, as illustrated
in the signal constellation in Figure 5.24, the optimum amplitude detector compares
the correlator output r with the four possible transmitted amplitude levels and
selects the amplitude level that is closest in Euclidean distance to r. Thus, the optimum
amplitude detector computes the distances
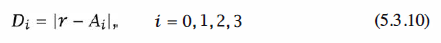
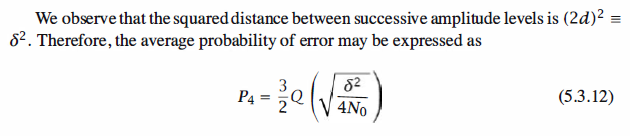

Matlab Coding,
1 % MATLAB script 2 3 echo on 4 clear; 5 SNRindB1=0:1:12; 6 SNRindB2=0:0.1:12; 7 for i=1:length(SNRindB1), 8 % simulated error rate 9 smld_err_prb(i)=smldPe58(SNRindB1(i)); 10 echo off; 11 end; 12 echo on; 13 for i=1:length(SNRindB2), 14 % signal-to-noise ratio 15 SNR_per_bit=exp(SNRindB2(i)*log(10)/10); 16 % theoretical error rate 17 theo_err_prb(i)=(3/2)*Qfunct(sqrt((4/5)*SNR_per_bit)); 18 echo off; 19 end; 20 echo on; 21 % Plotting commands follow. 22 semilogy(SNRindB1,smld_err_prb,'*'); 23 hold 24 semilogy(SNRindB2,theo_err_prb); 25 xlabel('SNR') 26 27 28 function [p]=smldPe58(snr_in_dB) 29 % [p]=smldPe58(snr_in_dB) 30 % SMLDPE58 simulates the probability of error for the given 31 % snr_in_dB, signal to noise ratio in dB. 32 d=1; 33 SNR=exp(snr_in_dB*log(10)/10); % signal to noise ratio per bit 34 sgma=sqrt((5*d^2)/(4*SNR)); % sigma, standard deviation of noise 35 N=10000; % number of symbols being simulated
36 % Generation of the quaternary data source follows. 37 for i=1:N, 38 temp=rand; % a uniform random variable over (0,1) 39 if (temp<0.25), 40 dsource(i)=0; % With probability 1/4, source output is "00." 41 elseif (temp<0.5), 42 dsource(i)=1; % With probability 1/4, source output is "01." 43 elseif (temp<0.75), 44 dsource(i)=2; % With probability 1/4, source output is "10." 45 else 46 dsource(i)=3; % With probability 1/4, source output is "11." 47 end 48 end;
49 % detection, and probability of error calculation 50 numoferr=0; 51 for i=1:N, 52 % the matched filter outputs 53 if (dsource(i)==0), 54 r=-3*d+gngauss(sgma); % if the source output is "00" 55 elseif (dsource(i)==1), 56 r=-d+gngauss(sgma); % if the source output is "01" 57 elseif (dsource(i)==2) 58 r=d+gngauss(sgma); % if the source output is "10" 59 else 60 r=3*d+gngauss(sgma); % if the source output is "11" 61 end; 62 % Detector follows. 63 if (r<-2*d), 64 decis=0; % Decision is "00." 65 elseif (r<0), 66 decis=1; % Decision is "01." 67 elseif (r<2*d), 68 decis=2; % Decision is "10." 69 else 70 decis=3; % Decision is "11." 71 end; 72 if (decis~=dsource(i)), % If it is an error, increase the error counter. 73 numoferr=numoferr+1; 74 end; 75 end; 76 p=numoferr/N; % probability of error estimate
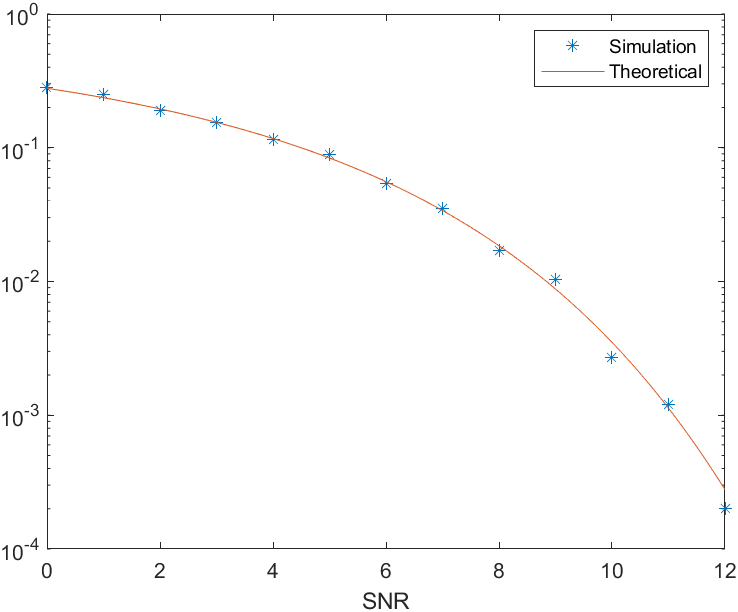
Simulation Result
Reference,
1. <<Contemporary Communication System using MATLAB>> - John G. Proakis